备考浙教版中考数学题型专项训练 图形的性质选择题专练
试卷更新日期:2022-05-17 类型:三轮冲刺
一、单选题
-
1. 如图,C、D是线段AB上两点,M、N分别是线段AD,BC的中点,下列结论:
①若AD=BM,则AB=3BD;②AC=BD,则AM=BN;③AC﹣BD=2(MC﹣DN);④2MN=AB﹣CD.
其中正确的结论是( )
 A、①②③ B、③④ C、①②④ D、①②③④2. 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( )
A、①②③ B、③④ C、①②④ D、①②③④2. 如图,在平行四边形ABCD中,AB=5,BC=8,∠ABC和∠BCD的角平分线分别交AD于点E和F,若BE=6,则CF=( ) A、6 B、8 C、10 D、133. 如图,一块长方形场地 的长 与宽 的比是 : , , ,垂足分别是 、 两点.现计划在四边形 区域种植花草,则四边形 与长方形 的面积比等于( )
A、6 B、8 C、10 D、133. 如图,一块长方形场地 的长 与宽 的比是 : , , ,垂足分别是 、 两点.现计划在四边形 区域种植花草,则四边形 与长方形 的面积比等于( ) A、1:3 B、2:3 C、1:2 D、1:44. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )
A、1:3 B、2:3 C、1:2 D、1:44. 如图,在矩形 中, 、 分别是边 、 上的点, ,连接 、 , 与对角线 交于点 ,且 , , ,则 的长为( )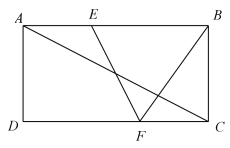 A、 B、 C、4 D、65. 如图所示,直线 ,点 在直线AB上,点 在直线CD上, , ,则 ( )
A、 B、 C、4 D、65. 如图所示,直线 ,点 在直线AB上,点 在直线CD上, , ,则 ( ) A、45° B、50° C、55° D、60°6. 如图,边长为5的等边三角形 中,M是高 所在直线上的一个动点,连接 ,将线段 绕点B逆时针旋转 得到 ,连接 .则在点M运动过程中,线段 长度的最小值是( )
A、45° B、50° C、55° D、60°6. 如图,边长为5的等边三角形 中,M是高 所在直线上的一个动点,连接 ,将线段 绕点B逆时针旋转 得到 ,连接 .则在点M运动过程中,线段 长度的最小值是( ) A、 B、1 C、2 D、7. 如图所示: 把两个正方形放置在周长为 的长方形 内, 两个正方形的重叠部分的周长为 (图中阴影部分所示), 则这两个正方形的周长和可用代数式表示为( )
A、 B、1 C、2 D、7. 如图所示: 把两个正方形放置在周长为 的长方形 内, 两个正方形的重叠部分的周长为 (图中阴影部分所示), 则这两个正方形的周长和可用代数式表示为( )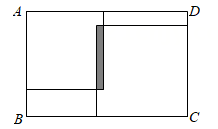 A、 B、 C、 D、8. 已知,点C在直线 AB 上, AC=a , BC=b ,且 a≠b ,点 M是线段 AB 的中点,则线段 MC的长为( )A、 B、 C、 或 D、 或9. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动;第一次将点A向左移动3个单位长度到达点 ,第二次将点A向右移动6个单位长度到达点 ,第三次将点 向左移动9个单位长度到达点 ,按照这种移动规律移动下去,第n次移动到点 ,如果点 与原点的距离不小于17,那么n的最小值是( )
A、 B、 C、 D、8. 已知,点C在直线 AB 上, AC=a , BC=b ,且 a≠b ,点 M是线段 AB 的中点,则线段 MC的长为( )A、 B、 C、 或 D、 或9. 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动;第一次将点A向左移动3个单位长度到达点 ,第二次将点A向右移动6个单位长度到达点 ,第三次将点 向左移动9个单位长度到达点 ,按照这种移动规律移动下去,第n次移动到点 ,如果点 与原点的距离不小于17,那么n的最小值是( )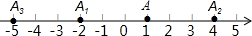 A、9 B、10 C、11 D、1210. 如图,在正方形ABCD中,点M、N分别为边CD、BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN的中点,连接PQ、BQ,若AB=8,DM=2,给出以下结论:①AM⊥DN;②∠MAN=∠BAN;③△PQN≌△BQN;④PQ=5。其中正确的结论有( )(填上所有正确结论的序号)
A、9 B、10 C、11 D、1210. 如图,在正方形ABCD中,点M、N分别为边CD、BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN的中点,连接PQ、BQ,若AB=8,DM=2,给出以下结论:①AM⊥DN;②∠MAN=∠BAN;③△PQN≌△BQN;④PQ=5。其中正确的结论有( )(填上所有正确结论的序号)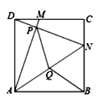 A、②③ B、①④ C、①②③ D、①②③④11. 如图,以Rt 的各边为边分别向外作正方形, ,连接 ,点 为 的中点,连接 ,若要求出 的面积,只需知道( )
A、②③ B、①④ C、①②③ D、①②③④11. 如图,以Rt 的各边为边分别向外作正方形, ,连接 ,点 为 的中点,连接 ,若要求出 的面积,只需知道( )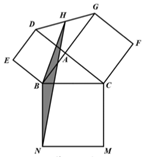 A、 的面积 B、正方形 的面积 C、正方形 的面积 D、正方形 的面积12. 如下图,在四边形中, , , , 点分别在边上,若 , 则 ( )
A、 的面积 B、正方形 的面积 C、正方形 的面积 D、正方形 的面积12. 如下图,在四边形中, , , , 点分别在边上,若 , 则 ( ) A、 B、 C、 D、13. 如图,在平行四边形OABC中,边OC在x轴上,点A(1,),点C(3,0).按以下步骤作图:分别以点B,C为圆心,大于BC的长为半径作弧,两弧相交于E,F两点;作直线EF,交AB于点H;连接OH,则OH的长为( )
A、 B、 C、 D、13. 如图,在平行四边形OABC中,边OC在x轴上,点A(1,),点C(3,0).按以下步骤作图:分别以点B,C为圆心,大于BC的长为半径作弧,两弧相交于E,F两点;作直线EF,交AB于点H;连接OH,则OH的长为( ) A、 B、 C、2 D、214. 如图,点A、B、C在一条直线上,△ABD和△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④PQ∥AC.其中结论正确的有( )
A、 B、 C、2 D、214. 如图,点A、B、C在一条直线上,△ABD和△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④PQ∥AC.其中结论正确的有( ) A、1个 B、2个 C、3个 D、4个15. 如图,正方形边长为4,点在边上运动(不含端点),以为边作等腰直角三角形 , ∠AEF=90°,连接.下面四个说法中有几个正确( )
A、1个 B、2个 C、3个 D、4个15. 如图,正方形边长为4,点在边上运动(不含端点),以为边作等腰直角三角形 , ∠AEF=90°,连接.下面四个说法中有几个正确( )①当时,;②当时,点 , , 共线;③当三角形与三角形面积相等时,则DE=;④当平分∠EAF时,则DE=
 A、1个 B、2个 C、3个 D、4个16. 如图,在平行四边形ABCD中,点E在AD的延长线上,点F在线段AB上,依次连接EB、EC、FC,当点F从点B出发向点A运动时(点F不与B,A重合),△CHE的面积与△BFH的面积差的变化情况是( )
A、1个 B、2个 C、3个 D、4个16. 如图,在平行四边形ABCD中,点E在AD的延长线上,点F在线段AB上,依次连接EB、EC、FC,当点F从点B出发向点A运动时(点F不与B,A重合),△CHE的面积与△BFH的面积差的变化情况是( ) A、先变小,再变大 B、一直不变 C、一直变小 D、一直变大17. 如图,在平行四边形ABCD纸片中,∠BAD=45°,AB=10.将纸片折叠,使得点A的对应点A'落在BC边上,折痕EF交AB、AD、AA'分别于点E、F、G. 继续折叠纸片,使得点C的对应点C'落在A'F上.连接GC',则GC'的最小值为( )
A、先变小,再变大 B、一直不变 C、一直变小 D、一直变大17. 如图,在平行四边形ABCD纸片中,∠BAD=45°,AB=10.将纸片折叠,使得点A的对应点A'落在BC边上,折痕EF交AB、AD、AA'分别于点E、F、G. 继续折叠纸片,使得点C的对应点C'落在A'F上.连接GC',则GC'的最小值为( ) A、 B、 C、 D、18. 由四个全等的直角三角形和一个小正方形组成的大正方形 ABCD 如图所示,延长 AH 交 CD 于点P,若 AP⊥HF,AP= 5 , 则小正方形边长 GF 的长是( )
A、 B、 C、 D、18. 由四个全等的直角三角形和一个小正方形组成的大正方形 ABCD 如图所示,延长 AH 交 CD 于点P,若 AP⊥HF,AP= 5 , 则小正方形边长 GF 的长是( ) A、 B、 C、3 D、19. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )
A、 B、 C、3 D、19. 如图,正方形ABCD的边长是 , 以正方形对角线的一半OA为边作正六边形,其中一边与正方形的边CD交于点E,再以点O为圆心OE为半径画弧交AD于点F,则图中阴影部分的的面积为( )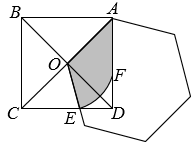 A、 B、 C、 D、20. 如图, △ABC是⊙O的内接三角形,将劣弧AC沿AC折叠后刚好经过弦BC 的中点 D.若 AC=6,∠C=60°,则⊙O的半径长为( )
A、 B、 C、 D、20. 如图, △ABC是⊙O的内接三角形,将劣弧AC沿AC折叠后刚好经过弦BC 的中点 D.若 AC=6,∠C=60°,则⊙O的半径长为( ) A、 B、 C、 D、21. 矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )
A、 B、 C、 D、21. 矩形ABCD中,AB=12,BC=8,将矩形沿MN折叠,使点C恰好落在AD边的中点F处,以矩形对称中心O点为圆心的圆与FN相切于点G,则⊙O的半径为( )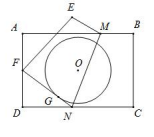 A、3.6 B、 C、3.5 D、22. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )
A、3.6 B、 C、3.5 D、22. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )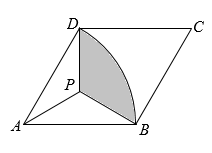 A、 B、 C、 D、23. 如图,在矩形ABCD中,点E在CD边上,连接AE,将 沿AE翻折,使点D落在BC边的点F处,连接AF,在AF上取点O,以O为圆心,线段OF的长为半径作⊙O,⊙O与AB,AE分别相切于点G,H,连接FG,GH.则下列结论错误的是( )
A、 B、 C、 D、23. 如图,在矩形ABCD中,点E在CD边上,连接AE,将 沿AE翻折,使点D落在BC边的点F处,连接AF,在AF上取点O,以O为圆心,线段OF的长为半径作⊙O,⊙O与AB,AE分别相切于点G,H,连接FG,GH.则下列结论错误的是( ) A、 B、四边形EFGH是菱形 C、 D、24. 如图,已知AB和CD是⊙O的两条等弦,OM⊥AB、ON⊥CD,垂足分别为M、N,BA、DC的延长线交于点P,连接OP.下列四个说法:①=;②OM=ON;③PA=PC;④∠BPO=∠DPO;正确的个数是( )
A、 B、四边形EFGH是菱形 C、 D、24. 如图,已知AB和CD是⊙O的两条等弦,OM⊥AB、ON⊥CD,垂足分别为M、N,BA、DC的延长线交于点P,连接OP.下列四个说法:①=;②OM=ON;③PA=PC;④∠BPO=∠DPO;正确的个数是( ) A、1 B、2 C、3 D、425. 如图, 中, 于点 是半径为2的上一动点, 连结 , 若是的中点, 连结 , 则长的最大值为 ( )
A、1 B、2 C、3 D、425. 如图, 中, 于点 是半径为2的上一动点, 连结 , 若是的中点, 连结 , 则长的最大值为 ( ) A、3 B、 C、4 D、26. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A、3 B、 C、4 D、26. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )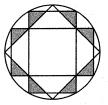 A、1 B、 C、 D、27. 如图,等边△ABC内接于⊙O,D是上任一点(不与B、C重合),连接BD、CD,AD交BC于E,CF切⊙O于点C,AF⊥CF交⊙O于点G.下列结论:①∠ADC=60°;②DB2=DE•DA;③若AD=2,则四边形ABDC的面积为;④若CF=2 , 则图中阴影部分的面积为.正确的个数为( )
A、1 B、 C、 D、27. 如图,等边△ABC内接于⊙O,D是上任一点(不与B、C重合),连接BD、CD,AD交BC于E,CF切⊙O于点C,AF⊥CF交⊙O于点G.下列结论:①∠ADC=60°;②DB2=DE•DA;③若AD=2,则四边形ABDC的面积为;④若CF=2 , 则图中阴影部分的面积为.正确的个数为( ) A、1个 B、2个 C、3个 D、4个28. 如图,点C,D是劣弧 上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则 所在圆的半径长为( )
A、1个 B、2个 C、3个 D、4个28. 如图,点C,D是劣弧 上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则 所在圆的半径长为( ) A、 B、 C、2 D、29. 在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称, 与AE交于点F,连接 , , 下列结论: ; 为等腰直角三角形; ; 其中正确的是( )
A、 B、 C、2 D、29. 在正方形ABCD中,点E为BC边的中点,点 与点B关于AE对称, 与AE交于点F,连接 , , 下列结论: ; 为等腰直角三角形; ; 其中正确的是( ) A、 B、 C、 D、30. 如图,直线 与双曲线 交于 , ,直线AB交x轴于 ,下列命题:① ;②当 时, ;③若 为线段AB的中点,则 ,其中正确的命题有( )
A、 B、 C、 D、30. 如图,直线 与双曲线 交于 , ,直线AB交x轴于 ,下列命题:① ;②当 时, ;③若 为线段AB的中点,则 ,其中正确的命题有( ) A、①② B、②③ C、①③ D、①②③31. 近几年来,在欧美等国家流行一种“数独”推理游戏,游戏规则如下:①9×9的九宫格子中,分成9个3×3的小九宫格,用1,2,3,…,9这9个数字填满整个格子,且每个格子只能填一个数;②每一行与每一列以及每个小九宫格里分别都有1,2,3,…9的所有数字.根据图中已填入的数字,可以判断A处填入的数字是( )
A、①② B、②③ C、①③ D、①②③31. 近几年来,在欧美等国家流行一种“数独”推理游戏,游戏规则如下:①9×9的九宫格子中,分成9个3×3的小九宫格,用1,2,3,…,9这9个数字填满整个格子,且每个格子只能填一个数;②每一行与每一列以及每个小九宫格里分别都有1,2,3,…9的所有数字.根据图中已填入的数字,可以判断A处填入的数字是( )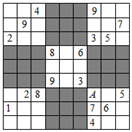 A、9 B、8 C、2 D、132. 等腰三角形ABC中,AB=AC , 记AB=x , 周长为y , 定义(x , y)为这个三角形的坐标,如图所示,直线 将第一象限划分为4个区域,下面四个结论中:
A、9 B、8 C、2 D、132. 等腰三角形ABC中,AB=AC , 记AB=x , 周长为y , 定义(x , y)为这个三角形的坐标,如图所示,直线 将第一象限划分为4个区域,下面四个结论中:①对于任意等腰三角形ABC , 其坐标不可能位于区域Ⅰ中;②对于任意等腰三角形ABC , 其坐标可能位于区域Ⅳ;③若三角形ABC是都能腰直角三角形,其坐标位于区域Ⅲ中;④图中点M所对应等腰三角形的底边比点N所对应等腰三角形的底边长所有正确的结论序号是( )
 A、①③ B、①③④ C、②④ D、①②③
A、①③ B、①③④ C、②④ D、①②③