备考浙教版中考数学题型专项训练 二次函数选择题专练
试卷更新日期:2022-05-17 类型:三轮冲刺
一、单选题
-
1. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为 ,其部分图象如图所示,下列结论:① ;②方程ax2+bx+c=0的两个根是 ,x2=3;③3a+c>0;④当y>0时,x的取值范围是 ;⑤当x<0时,y随x增大而增大,其中结论正确的个数是( )
 A、4个 B、3个 C、2个 D、5个2. 如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点D与点C关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则图中阴影部分的面积变化情况是( )
A、4个 B、3个 C、2个 D、5个2. 如图,二次函数 与x轴交于A、B两点,与y轴交于C点,点D与点C关于x轴对称,点P从点A出发向点D运动,点Q在DB上,且∠PCQ=45°,则图中阴影部分的面积变化情况是( )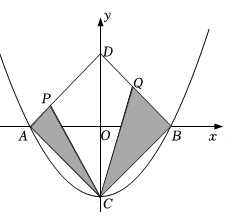 A、一直增大 B、始终不变 C、先减小后增大 D、先增大后减小3. 如图所示,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C.对称轴为直线x=l,直线y=﹣x+c与抛物线交于C,D两点,D点在x轴下方且横坐标小于3,现有下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)<a+b;④a<﹣1.其中正确的结论是( )
A、一直增大 B、始终不变 C、先减小后增大 D、先增大后减小3. 如图所示,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,与y轴交于点C.对称轴为直线x=l,直线y=﹣x+c与抛物线交于C,D两点,D点在x轴下方且横坐标小于3,现有下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)<a+b;④a<﹣1.其中正确的结论是( ) A、①②③ B、①②④ C、②③④ D、①③④4. 求二次函数 的图象如图所示,其对称轴为直线 ,与 轴的交点为 、 ,其中 ,有下列结论:① ;② ;③ ;④ ;⑤ ;其中,正确的结论有( )
A、①②③ B、①②④ C、②③④ D、①③④4. 求二次函数 的图象如图所示,其对称轴为直线 ,与 轴的交点为 、 ,其中 ,有下列结论:① ;② ;③ ;④ ;⑤ ;其中,正确的结论有( ) A、5 B、4 C、3 D、25. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(3,0),与y轴的交点B在(0,1)和(0,2)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc<0;②4a+2b+c>0;③5a+b+c=0;④ <b<1.其中正确结论的个数是( )
A、5 B、4 C、3 D、25. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(3,0),与y轴的交点B在(0,1)和(0,2)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc<0;②4a+2b+c>0;③5a+b+c=0;④ <b<1.其中正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个6. 抛物线 的对称轴是直线 ,其图象如图所示.下列结论:① ;② ;③若 和 是抛物线上的两点,则当 时, ;④抛物线的顶点坐标为 ,则关于 的方程 无实数根.其中正确结论的个数是( )
A、1个 B、2个 C、3个 D、4个6. 抛物线 的对称轴是直线 ,其图象如图所示.下列结论:① ;② ;③若 和 是抛物线上的两点,则当 时, ;④抛物线的顶点坐标为 ,则关于 的方程 无实数根.其中正确结论的个数是( ) A、4 B、3 C、2 D、17. 如图,抛物线y=ax2+bx+c与x轴的一个交点E在点(-3,0)和(-2,0)之间(包括这两点),顶点P是矩形ABCD上(包括边界和内部)的一个动点,则a的取值范围是( )
A、4 B、3 C、2 D、17. 如图,抛物线y=ax2+bx+c与x轴的一个交点E在点(-3,0)和(-2,0)之间(包括这两点),顶点P是矩形ABCD上(包括边界和内部)的一个动点,则a的取值范围是( ) A、 B、 C、 D、8. 如图是二次函数 图象的一部分,该图象过点 ,对称轴为直线 ,下列结论:① ;② ;③若 与 是抛物线上两点,则 ;④ ,其中正确的有( )
A、 B、 C、 D、8. 如图是二次函数 图象的一部分,该图象过点 ,对称轴为直线 ,下列结论:① ;② ;③若 与 是抛物线上两点,则 ;④ ,其中正确的有( ) A、1个 B、2个 C、3个 D、4个9. 拋物线 为常数 开口向下且过点 ,下列结论:(1) ;(2) ;(3) ;(4) ,若方程有两个不相等的实数根, 则 . 其中正确结论的个数是( )A、4 B、3 C、2 D、110. 如图,抛物线 与x轴交于点 ,其对称轴为直线 ,结合图象分析下列结论:① ;②当 时,y随x的增大而增大;③ ;④ ;⑤若m,n( )为方程 的两个根,则 且 .其中符合题意结论的个数是( )
A、1个 B、2个 C、3个 D、4个9. 拋物线 为常数 开口向下且过点 ,下列结论:(1) ;(2) ;(3) ;(4) ,若方程有两个不相等的实数根, 则 . 其中正确结论的个数是( )A、4 B、3 C、2 D、110. 如图,抛物线 与x轴交于点 ,其对称轴为直线 ,结合图象分析下列结论:① ;②当 时,y随x的增大而增大;③ ;④ ;⑤若m,n( )为方程 的两个根,则 且 .其中符合题意结论的个数是( )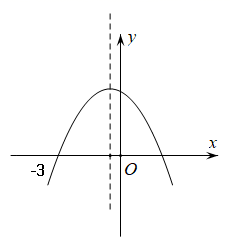 A、2个 B、3个 C、4个 D、511. 已知二次函数 ( )图象的对称轴为直线 ,部分图象如图所示,下列结论中:① ;② ;③ ;④若 为任意实数,则有 ;⑤当图象经过点 时,方程 的两根为 , ,则 ,其中正确的结论有( )
A、2个 B、3个 C、4个 D、511. 已知二次函数 ( )图象的对称轴为直线 ,部分图象如图所示,下列结论中:① ;② ;③ ;④若 为任意实数,则有 ;⑤当图象经过点 时,方程 的两根为 , ,则 ,其中正确的结论有( ) A、①②③ B、②③⑤ C、②③④⑤ D、②③④12. 小明研究二次函数 (b为常数)性质时,得到如下结论:
A、①②③ B、②③⑤ C、②③④⑤ D、②③④12. 小明研究二次函数 (b为常数)性质时,得到如下结论:①对于任意实数m,m(m-2b)≥1-2b始终成立,则b=1;②这个函数的顶点始终在抛物线 上;③在-1≤x≤5范围内,y的值最大时,x=-1,点(m1 , p)与点(m2 , p)(m1≠m2)在这个函数图象上,则m1+m2>4;④点(b-2n,y1)与点(b+n,y2)(n≠0)在这个函数图象上,则y1<y2其中错误的结论个数是( )
A、1 B、2 C、3 D、413. 已知抛物线y=a(x﹣3)2+过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切。正确的结论是( ) A、①③ B、①④ C、①③④ D、①②③④14. 点P(x1 , y1),Q(x2 , y2)在抛物线y=ax2-4ax+2(a>0)上,若对于t<x1<t+1,t+2<x2<t+3,都有y1≠y2 , 则t的取值范围是( )A、t≥1 B、t≤0 C、t≥1或t≤0 D、t≥1或t≤-115. 如图,在平面直角坐标系中,二次函数的图象与x轴交于A、C两点,与y轴交于点B,若P是x轴上一动点,点Q(0,2)在y轴上,连接PQ,则的最小值是( )
A、①③ B、①④ C、①③④ D、①②③④14. 点P(x1 , y1),Q(x2 , y2)在抛物线y=ax2-4ax+2(a>0)上,若对于t<x1<t+1,t+2<x2<t+3,都有y1≠y2 , 则t的取值范围是( )A、t≥1 B、t≤0 C、t≥1或t≤0 D、t≥1或t≤-115. 如图,在平面直角坐标系中,二次函数的图象与x轴交于A、C两点,与y轴交于点B,若P是x轴上一动点,点Q(0,2)在y轴上,连接PQ,则的最小值是( )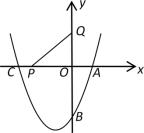 A、6 B、 C、 D、16. 如图所示,在平面直角坐标系中,抛物线y=-x2+2x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+AP的最小值为( ).
A、6 B、 C、 D、16. 如图所示,在平面直角坐标系中,抛物线y=-x2+2x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+AP的最小值为( ). A、3 B、 C、 D、17. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),与y轴的交点B在点(0,2)与点(0,3)之间(不包括这两点),对称轴为直线x=2.有以下结论:①abc<0;②5a+3b+c>0;③-<a<-;④若点M(-9a,y1),N(a,y2)在抛物线上,则y1<y2 . 其中正确结论的个数是( )
A、3 B、 C、 D、17. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),与y轴的交点B在点(0,2)与点(0,3)之间(不包括这两点),对称轴为直线x=2.有以下结论:①abc<0;②5a+3b+c>0;③-<a<-;④若点M(-9a,y1),N(a,y2)在抛物线上,则y1<y2 . 其中正确结论的个数是( ) A、1 B、2 C、3 D、418. 如图抛物线的对称轴为直线 , 与x轴一个交点在和之间,其部分图象如图所示.则下列结论:①;②;③;④ (t为实数);⑤点 , , 是该抛物线上的点,则 . 正确的个数有( )
A、1 B、2 C、3 D、418. 如图抛物线的对称轴为直线 , 与x轴一个交点在和之间,其部分图象如图所示.则下列结论:①;②;③;④ (t为实数);⑤点 , , 是该抛物线上的点,则 . 正确的个数有( ) A、4个 B、3个 C、2个 D、1个19. , 点是函数图象上任意一点,( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则20. 二次函数(a,b,c为常数,且)中的x与y的部分对应值如表.下列结论:①;②当时,y的值随x值的增大而减小③3是方程的一个根;④当时,.其中正确的个数为( )
A、4个 B、3个 C、2个 D、1个19. , 点是函数图象上任意一点,( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则20. 二次函数(a,b,c为常数,且)中的x与y的部分对应值如表.下列结论:①;②当时,y的值随x值的增大而减小③3是方程的一个根;④当时,.其中正确的个数为( )x
…
-1
0
1
3
…
y
…
-1
3
5
3
…
A、1个 B、2个 C、3个 D、4个21. 已知 , 为抛物线 图象上的两点,且 ,则下列说法正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则22. 如图是二次函数图象的y=ax2+bx+c一部分,图象过点A(-3,0),对称轴为直线x=-1。则以下结论错误的是( ) A、b2>4ac B、2a+b=0 C、a+b+c=0 D、5a<b23. 如图,二次函数的图象与x轴交于A,B两点,与y轴的正半轴交于点C,它的对称轴为直线.有下列结论:①;②;③;④当时,;⑤若、()是方程的两根,则方程的两根m、n(m<n)满足 , 且.其中,正确结论的个数是( )
A、b2>4ac B、2a+b=0 C、a+b+c=0 D、5a<b23. 如图,二次函数的图象与x轴交于A,B两点,与y轴的正半轴交于点C,它的对称轴为直线.有下列结论:①;②;③;④当时,;⑤若、()是方程的两根,则方程的两根m、n(m<n)满足 , 且.其中,正确结论的个数是( ) A、1 B、2 C、3 D、424. 对于题目:在平面直角坐标系中,直线分别与轴、轴交于两点,过点且平行轴的直线与过点且平行轴的直线相交于点 , 若抛物线与线段有唯一公共点,求的取值范围.甲的计算结果是;乙的计算结果是 , 则( )A、甲的结果正确 B、乙的结果正确 C、甲与乙的结果合在一起正确 D、甲与乙的结果合在一起也不正确25. 如图,二次函数y=ax2+bx+c(a≠0) 的图象的对称轴是直线 x=1 ,则以下四个结论中:① abc>0 ,② 2a+b=0 ,③ 4a+b2<4ac ,④ 3a+c<0 .正确的个数是( )
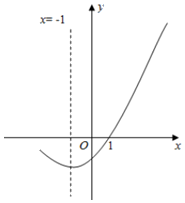
A、1 B、2 C、3 D、424. 对于题目:在平面直角坐标系中,直线分别与轴、轴交于两点,过点且平行轴的直线与过点且平行轴的直线相交于点 , 若抛物线与线段有唯一公共点,求的取值范围.甲的计算结果是;乙的计算结果是 , 则( )A、甲的结果正确 B、乙的结果正确 C、甲与乙的结果合在一起正确 D、甲与乙的结果合在一起也不正确25. 如图,二次函数y=ax2+bx+c(a≠0) 的图象的对称轴是直线 x=1 ,则以下四个结论中:① abc>0 ,② 2a+b=0 ,③ 4a+b2<4ac ,④ 3a+c<0 .正确的个数是( ) A、1 B、2 C、3 D、426. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图象给出下列结论:
A、1 B、2 C、3 D、426. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图象给出下列结论:①a+b+c=0;②a﹣2b+c>0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤a﹣b<m(am+b)(m为任意实数).
其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个27. 已知二次函数y=ax2+bx+c的图象过点A(2,n),当x>0时,y≥n,当x≤0时,y≥n+1,则a的值是( )A、﹣1 B、﹣ C、 D、128. 如图,二次函数()的函数图象经过点 , 且与轴交点的横坐标分别为、其中 , , 下列结论:①;②;③;④当()时,;⑤ , 其中正确的有( )
A、1个 B、2个 C、3个 D、4个27. 已知二次函数y=ax2+bx+c的图象过点A(2,n),当x>0时,y≥n,当x≤0时,y≥n+1,则a的值是( )A、﹣1 B、﹣ C、 D、128. 如图,二次函数()的函数图象经过点 , 且与轴交点的横坐标分别为、其中 , , 下列结论:①;②;③;④当()时,;⑤ , 其中正确的有( ) A、①②④ B、①③④ C、②④⑤ D、②③④29. 如图,已知抛物线y=x2-2x与直线y=-x+2交于A,B两点.点M是直线AB上的一个动点,将点M向左平移4个单位长度得到点N,若线段MN与抛物线只有一个公共点,则点M的横坐标xM的取值范围是( )
A、①②④ B、①③④ C、②④⑤ D、②③④29. 如图,已知抛物线y=x2-2x与直线y=-x+2交于A,B两点.点M是直线AB上的一个动点,将点M向左平移4个单位长度得到点N,若线段MN与抛物线只有一个公共点,则点M的横坐标xM的取值范围是( )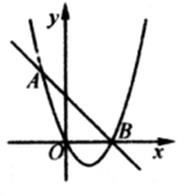 A、-2≤xM≤2 B、-2≤xM≤2且xM≤-1 C、-1≤xM<2 D、-1≤xM<2或xM=330. 如图,二次函数 的图象与 轴负半轴交于 ,对称轴为直线 .有以下结论:
A、-2≤xM≤2 B、-2≤xM≤2且xM≤-1 C、-1≤xM<2 D、-1≤xM<2或xM=330. 如图,二次函数 的图象与 轴负半轴交于 ,对称轴为直线 .有以下结论:① ;② ;③若点 , , 均在函数图象上,则 ;④若方程 的两根为 , 且 ,则 ;⑤点 , 是抛物线与 轴的两个交点,若在 轴下方的抛物线上存在一点 ,使得 ,则 的范围为 .其中结论正确的有( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个