备考浙教版中考数学题型专项训练 反比例函数填空题专练
试卷更新日期:2022-05-17 类型:三轮冲刺
一、填空题
-
1. 如图,点 是菱形的四个顶点,其中点 在反比例函数 的图象上,点 在反比例函数 的图象上,且点 关于原点成中心对称,点 的横坐标相等,则 的值为;过点 作AE// 轴交反比例函数 的图象于点 ,连结 并延长交 轴于点 ,连结 .若S△DOF=7,则 的值为 .
 2. 如图,位于平面直角坐标系中,点B在x轴正半轴上,点A及的中点D在反比例函数的图象上,点C在反比例函数的图象上,则k的值为.
2. 如图,位于平面直角坐标系中,点B在x轴正半轴上,点A及的中点D在反比例函数的图象上,点C在反比例函数的图象上,则k的值为. 3. 如图,已知 为反比例函数 图象上一点, 为 轴正半轴上一点,过点 作 轴交反比例函数图象于点 ,连结 , , 当 , 的面积等于2时, 的值为.
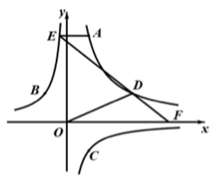
3. 如图,已知 为反比例函数 图象上一点, 为 轴正半轴上一点,过点 作 轴交反比例函数图象于点 ,连结 , , 当 , 的面积等于2时, 的值为.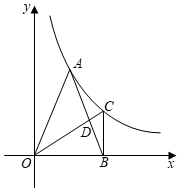 4. 如图,Rt△AOB中,∠OAB=90°,∠OBA=30°,顶点A在反比例函数y=图象上,若Rt△AOB的面积恰好被y轴平分,则进过点B的反比例函数的解析式为.
4. 如图,Rt△AOB中,∠OAB=90°,∠OBA=30°,顶点A在反比例函数y=图象上,若Rt△AOB的面积恰好被y轴平分,则进过点B的反比例函数的解析式为.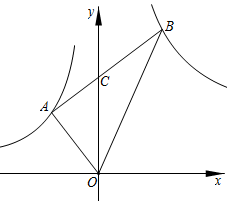 5. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴正半轴上,反比例函数的图象经过顶点C和对角线OB的中点D.作交y轴于点E.若的面积为12,则k的值为.
5. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴正半轴上,反比例函数的图象经过顶点C和对角线OB的中点D.作交y轴于点E.若的面积为12,则k的值为.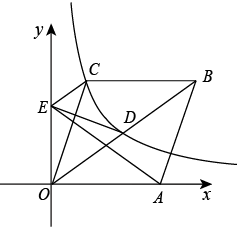 6. 如图,点P是反比例函数 图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= .
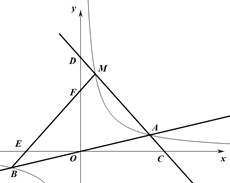
6. 如图,点P是反比例函数 图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB= . (1)、k的值是;(2)、若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是.7. 如图, 的顶点 的坐标为 在第一象限.反比例函数 和 的图象分别经过 , 两点,延长BC交 轴于点 .设 是反比例函数 图象上的动点.若 的面积是 面积的2倍, 的面积等于 ,则 的值为.
(1)、k的值是;(2)、若M(a,b)是该反比例函数图象上的点,且满足∠MBA<∠ABC,则a的取值范围是.7. 如图, 的顶点 的坐标为 在第一象限.反比例函数 和 的图象分别经过 , 两点,延长BC交 轴于点 .设 是反比例函数 图象上的动点.若 的面积是 面积的2倍, 的面积等于 ,则 的值为. 8. 如图,已知等边 , 顶点在双曲线上,点的坐标为 . 过作交双曲线于点 , 过作交轴于点 , 得到第二个等边;过作交双曲线于点 , 过作交轴于点 , 得到第三个等边;以此类推,…,则点的坐标为 .
8. 如图,已知等边 , 顶点在双曲线上,点的坐标为 . 过作交双曲线于点 , 过作交轴于点 , 得到第二个等边;过作交双曲线于点 , 过作交轴于点 , 得到第三个等边;以此类推,…,则点的坐标为 . 9. 如图,直线 与坐标轴交于A,B两点,交反比例 的图象于C,D两点,且 ,点E是直线AB上一点,连接OE,以OE为边在OE右侧作直角三角形OEF, , ,若边OF交反比例函数图象于点G, ,则k值为 , 点E的坐标是.
9. 如图,直线 与坐标轴交于A,B两点,交反比例 的图象于C,D两点,且 ,点E是直线AB上一点,连接OE,以OE为边在OE右侧作直角三角形OEF, , ,若边OF交反比例函数图象于点G, ,则k值为 , 点E的坐标是. 10. 已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是 .11. 如图,矩形OABC的顶点A,C分别在x轴,y轴正半轴上,反比例函数 的图象分别与矩形OABC两边AB,BC交于点D,E,沿直线DE将△DBE翻折得到△DFE,且点F恰好落在直线OA上.下列四个结论:① ;② ;③ ;④ .其中结论正确的有.(仅填序号即可)
10. 已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是 .11. 如图,矩形OABC的顶点A,C分别在x轴,y轴正半轴上,反比例函数 的图象分别与矩形OABC两边AB,BC交于点D,E,沿直线DE将△DBE翻折得到△DFE,且点F恰好落在直线OA上.下列四个结论:① ;② ;③ ;④ .其中结论正确的有.(仅填序号即可) 12. 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是.
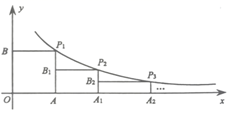
12. 如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为y= ,在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.设P(t,0),当O′B′与双曲线有交点时,t的取值范围是.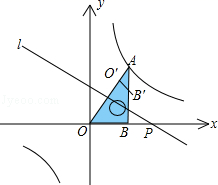 13. 如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An﹣1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn , 连接P1P2、P2P3、…、Pn﹣1Pn , 过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是
13. 如图,在x轴正半轴上依次截取OA1=A1A2=A2A…An﹣1An(n为正整数),过点A1、A2、A3、…、An分别作x轴的垂线,与反比例函数y= (x>0)交于点P1、P2、P3、…、Pn , 连接P1P2、P2P3、…、Pn﹣1Pn , 过点P2、P3、…、Pn分别向P1A1、P2A2、…、Pn﹣1An﹣1作垂线段,构成的一系列直角三角形(见图中阴影部分)的面积和是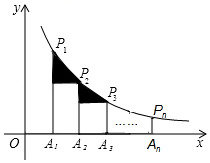 14. 如图,在矩形AOBC中,OB=8,OA=6,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 (k>0)的图象与AC边交于点E,将△CEF沿EF对折后,C点恰好落在OB上的点D处,则k的值为.
14. 如图,在矩形AOBC中,OB=8,OA=6,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B,C重合),过F点的反比例函数 (k>0)的图象与AC边交于点E,将△CEF沿EF对折后,C点恰好落在OB上的点D处,则k的值为. 15. 如图,点 在反比例函数图象 上,以 为直径的圆交该双曲线于点 ,交 轴于点 ,若 ,则该圆的直径长是.
15. 如图,点 在反比例函数图象 上,以 为直径的圆交该双曲线于点 ,交 轴于点 ,若 ,则该圆的直径长是.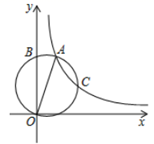 16. 如图,A、B两点是反比例函数y1= 与一次函数y=2x的交点,点C在反比例函数y2= 上,连接OC,过点A作AD⊥x轴交OC于点D,连接BD.若AD=BD,OC=3OD,则k= .
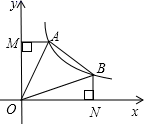
16. 如图,A、B两点是反比例函数y1= 与一次函数y=2x的交点,点C在反比例函数y2= 上,连接OC,过点A作AD⊥x轴交OC于点D,连接BD.若AD=BD,OC=3OD,则k= .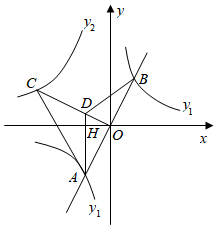 17. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.
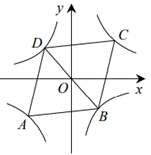
17. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.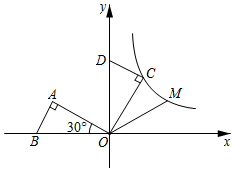 18. 如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点C在直线y=x_上,点B的坐标为(2,1)将菱形ABCD沿直线y=x平移,当点B,D同时落在反比例函数y= (x>0)的图象上时,菱形沿直线y=x平移的距离为。
18. 如图,在平面直角坐标系中,菱形ABCD的顶点A与原点O重合,点C在直线y=x_上,点B的坐标为(2,1)将菱形ABCD沿直线y=x平移,当点B,D同时落在反比例函数y= (x>0)的图象上时,菱形沿直线y=x平移的距离为。 19. 如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴正半轴上,顶点B,C在第一象限,顶点D的坐标 . 反比例函数 (常数 , )的图象恰好经过正方形ABCD的两个顶点,则k的值是.
19. 如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴正半轴上,顶点B,C在第一象限,顶点D的坐标 . 反比例函数 (常数 , )的图象恰好经过正方形ABCD的两个顶点,则k的值是.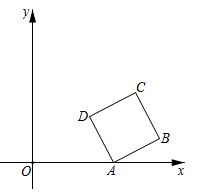 20. 如图,一次函数 与反比例函数 ( )的图象交于点 ,过点 作 ,交 轴于点 ;作 ,交反比例函数图象于点 ;过点 作 交 轴于点 ;再作 ,交反比例函数图象于点 ,依次进行下去,……,则点 的横坐标为 .
20. 如图,一次函数 与反比例函数 ( )的图象交于点 ,过点 作 ,交 轴于点 ;作 ,交反比例函数图象于点 ;过点 作 交 轴于点 ;再作 ,交反比例函数图象于点 ,依次进行下去,……,则点 的横坐标为 .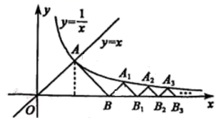 21. 如图,在平面直角坐标系中,矩形ABCD的边分别平行于坐标轴,原点O恰好为矩形对角线的交点,反比例函数y= 的图象与矩形ABCD的边交于点M、N、P、Q,记矩形ABCD的面积为S1 , 四边形MNPQ的面积为S2 , 若S1=3S2 , 则MN:MQ的值为.
21. 如图,在平面直角坐标系中,矩形ABCD的边分别平行于坐标轴,原点O恰好为矩形对角线的交点,反比例函数y= 的图象与矩形ABCD的边交于点M、N、P、Q,记矩形ABCD的面积为S1 , 四边形MNPQ的面积为S2 , 若S1=3S2 , 则MN:MQ的值为. 22. 如图,在平面直角坐标系中, 为坐标原点, 在 轴正半轴上,四边形 为平行四边形,反比例函数 的图象经过点 与边 相交于点 ,若 , ,则 .
22. 如图,在平面直角坐标系中, 为坐标原点, 在 轴正半轴上,四边形 为平行四边形,反比例函数 的图象经过点 与边 相交于点 ,若 , ,则 . 23. 在平面直角坐标系 中,点 , , 在双曲线 上,且 , .则下列结论正确的有.(填写相应的序号即可)
23. 在平面直角坐标系 中,点 , , 在双曲线 上,且 , .则下列结论正确的有.(填写相应的序号即可)①若 且 ,则 为等腰三角形;
②若 且 ,则 为直角三角形;
③若 为等腰三角形,则 且 ;
④若 为直角三角形,则 且 .
24. 如图,在平面直角坐标系中,直线 与双曲线 相交于 、 两点,其中 点 ,点 为 点下方直线 上一动点,直线 ,分别与直线 、双曲线 、 轴交于 、 、 三点,则 的最大值是. 25. 在平面直角坐标系中,已知点 ,点 ,则线段 的长度的最小值是 .26. 如图,直线 与双曲线 交于 、 两点,连接 、 , 轴于 , 轴于 ,设 , 的解析式分别为 , ,现有以下结论:
25. 在平面直角坐标系中,已知点 ,点 ,则线段 的长度的最小值是 .26. 如图,直线 与双曲线 交于 、 两点,连接 、 , 轴于 , 轴于 ,设 , 的解析式分别为 , ,现有以下结论:① ;② ;③若 ,则 ;④ 有最小值.
其中正确的是.(写出所有正确结论的序号)
 27. 如图,函数 ( 为常数, )的图象与过原点的 的直线相交于 , 两点,点 是第一象限内双曲线上的动点(点 在点 的左侧),直线 分别交 轴, 轴于 , 两点,连接 分别交 轴, 轴于点 , ,现有以下四个结论:① 与 的面积相等;②若 于点 ,则 ;③若点 的横坐标为1, 为等边三角形,则 ;④若 ,则 .其中正确的结论的序号是.
27. 如图,函数 ( 为常数, )的图象与过原点的 的直线相交于 , 两点,点 是第一象限内双曲线上的动点(点 在点 的左侧),直线 分别交 轴, 轴于 , 两点,连接 分别交 轴, 轴于点 , ,现有以下四个结论:① 与 的面积相等;②若 于点 ,则 ;③若点 的横坐标为1, 为等边三角形,则 ;④若 ,则 .其中正确的结论的序号是.