辽宁省抚顺市顺城区2022年初中毕业生第二次质量调查数学试题

试卷更新日期：2022-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. -2022的绝对值是（）

A、2022 B、-2022 C、 $\frac{1}{2022}$ D、- $\frac{1}{2022}$

查看试题解析
2. 如图所示的几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，正确的是（）．

A、 $2 x \cdot 3 x^{2} = 5 x^{3}$ B、 $x^{4} + x^{2} = x^{6}$ C、 ${(x^{2} y)}^{3} = x^{6} y^{3}$ D、 ${(x + 1)}^{2} = x^{2} + 1$

查看试题解析
4. 某校为了纪念抗美援朝70周年，举行了主题为“捍卫和平，让历史照亮未来”的演讲比赛，其中九年级的5位参赛选手的比赛成绩（单位：分）分别为：85，93，87，95，90，则这5个数据的中位数和平均数分别为（）

A、90，93 B、93，90 C、95，90 D、90，90

查看试题解析
5. 下列调查适合抽样调查的是（）

A、审核稿件中的错别字 B、对某校九年级各班卫生死角进行调查 C、对某班同学的视力情况进行调查 D、对全国中学生目前睡眠情况进行调查

查看试题解析
6. 如图，把一块等腰直角三角板的直角顶点放在直尺的一边上，如果∠1=40°，那么∠2=（）

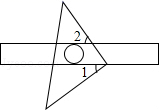A、40° B、45° C、50° D、60°

查看试题解析
7. 如图，以矩形ABCD的顶点A为圆心，适当的长为半径画弧，分别交AD、AB于点M、N，分别以点M、N为圆心，以大于 $\frac{1}{2}$ MN的长为半径画弧，两弧在∠DAB内部交于点P，作射线AP，交CD于点E，连接BE．若AB＝7，AD＝4，则BE的长度为（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，△ABC内接于⊙O，∠ACB＝15°，AE是⊙O的直径，点D在 $\overset{⌢}{B E}$ 上，连接CE、DE、BD，则∠BDE的度数是（）

A、105° B、115° C、120° D、130°

查看试题解析
9. 如图，在Rt△ABC中，∠ACB＝90°，D、E分别是AB、AC的中点，连接CD、DE，过E作EF∥DC交BC的延长线于F，若△ABC的周长是14，AC的长为4，则四边形CDEF的周长是（）

A、7 B、8 C、10 D、14

查看试题解析
10. 在△ABC中，AB＝AC，BC＝4，∠BAC＝120°，P为线段CA延长线上一动点，连接PB，将线段PB绕点P逆时针旋转120°，得到线段PD，连接DB、DC、DB交PC于点M，设线段AP＝x，△BCD的面积为y，则能反映y与x之间函数关系的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

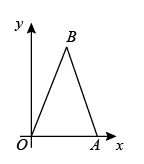
11. 当今5G的最低传输速率相当于每秒传输2500000个汉字，将数字2500000用科学记数法为．

查看试题解析
12. 因式分解： $12 - 3 x^{2} =$ .

查看试题解析
13. 不等式6x+1＞2x﹣3的解集是．

查看试题解析
14. 关于x的一元二次方程mx²﹣2x+1＝0有两个不相等的实数根，则实数m的取值范围是 .

查看试题解析
15. 一个不透明的口袋中有红桃扑克牌与黑桃扑克牌共20张，它们除花色外都相同，将口袋中的扑克牌搅拌均匀，从中随机摸出一张，记下花色后再放回口袋中，不断重复这一过程，实验共摸了50次，发现有20次摸到的是红桃扑克牌，则这个口袋中大约有张红桃扑克牌．

查看试题解析
16. 如图，△AOB三个顶点的坐标分别为A(4，0)，O(0，0)，B(2，6)，以点O为位似中心，将△AOB在第一象限缩小，若点B的对应点 $B^{'}$ 的坐标(1，3)，则 $\frac{S_{△ A^{'} O B^{'}}}{S_{△ A O B}}$ 的比值为．

查看试题解析
17. 如图，点A在反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）的图象上，AB⊥x轴于B，点C在x轴上且在点B右侧，点D在第一象限，DC⊥x轴，连接DB，若∠DBC＝∠OAB，DC＝OB＝3，反比例函数的图象恰好经过BD中点E，则k的值为．

查看试题解析
18. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AC＝6，点M是射线AC上的一个动点，MC＝1，连接BM，以AB为边在AB的上方作∠ABE＝∠AMB，直线BE交AC的延长线于点F，则CF＝．

查看试题解析

三、解答题

19. 先化简，再求值： $\frac{a^{2} - 4 a + 4}{a - 1} \div \frac{a^{2} - 4}{a^{2} - 1} - \frac{2 - a}{a + 2}$ ，其中a＝ $2 - \sqrt{3}$ ．

查看试题解析
20. 某校为发展学生的兴趣爱好，决定在校内开展第二课程，第二课程有：厨艺、插花、种植、陶艺，要求每名学生必须选修且只能选修一门课程，为保证课程的有效实施，学校随机对部分学生选择课程情况进行了一次调查，并将调查结果绘制成如下不完整的统计图．

根据以上信息，解答下列问题：

(1)、学校这次调查共抽取 ▲ 人，补全条形统计图；

(2)、该校有1000名学生，请你估计选择“厨艺”课程的学生有多少名；

(3)、选择“插花”课程的学生中，七（1）班和七（2）班各有2名同学成绩比较优异，学校准备从这4人中随机抽取2人在学期末汇报中进行展示，请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率．

查看试题解析
21. 某学校举办首届校园“数学文化节”，决定购买圆规和签字笔作为奖品，已知圆规的单价比签字笔的单价多5元，用400元购买的圆规个数和用150元购买的签字笔个数相同．

(1)、求圆规和签字笔的单价分别是多少元？

(2)、学校准备一次性购买圆规和签字笔两种奖品共120个，但总费用不超过600元．那么最多可购买多少个圆规？

查看试题解析
22. 如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角为45°，沿斜坡走13米到达斜坡上点D，在此处测得树顶端点B的仰角为31°，且斜坡AF的坡度为1：2.4．

(1)、求小明从点A到点D的过程中，他上升的高度；

(2)、大树BC的高度约为多少米？（参考数据：sin31°＝0.52，cos31°＝0.86，tan31°≈0.60）

查看试题解析
23. 如图，四边形ABCD是⊙O的内接四边形，其中∠ADC＝90°，在CD的延长线上有一点E，连接AE，且∠DAE＝∠ABD．

(1)、求证：AE与⊙O相切；

(2)、若AD＝2，CD＝4DE，求⊙O的半径．

查看试题解析
24. 某团体设计生产了一批运动服，每套的成本是65元，为了合理定价，先投放市场进行试销，要求批发价不得低于成本，据市场调查，每天的销售量y（件）与批发价x（元）之间的关系如图所示：

(1)、设批发价为x（元），每天的销售量为y（件），请写出y与x的函数关系式，并求出当批发价为80元时，每天的销量是多少？

(2)、求出每天的销售利润w（元）与批发价x（元）之间的函数关系式；

(3)、如果该企业每天的成本不超过39000元，那么批发价为多少元时，每天的销售利润最大？最大利润是多少？（每天的成本＝每套成本×每天的销售量）

查看试题解析
25. 如图，在△ABC中，∠ACB＝90°，AC＝BC，点D是直线BC上一点，作直线AD，过点B作BE⊥AD，垂足为点E，连接CE．

(1)、当点D在如图1的位置时，请直接写出线段EA、EB、EC之间的数量关系；

(2)、当点D在如图2的位置时，（1）中的结论是否成立，若成立，请完成证明，若不成立，请写出你的结论并说明理由；

(3)、当点E是线段AD中点时，请直接写出tan∠ADC的值．

查看试题解析
26. 抛物线y＝ax²+2x+c与x轴交于点A(﹣2，0)和点B，与y轴交于点C(0，6)，点D(m，0)是x轴上一点，过点D作直线DF⊥x轴，交直线BC于点E，交抛物线于点F．

(1)、求抛物线的解析式；

(2)、如图，连接BF，当tan∠FBC＝ $\frac{1}{2}$ 时，求出点E的坐标；

(3)、当△CEF是等腰三角形时，请直接写出点F的坐标．

查看试题解析