辽宁省抚顺市抚顺县2022年九年级下学期数学一模试卷
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. ﹣2的倒数是( )A、2 B、1 C、- D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图所示的几何体,它的左视图正确的是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图所示的几何体,它的左视图正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 某校为了解学生睡眠情况,随机调查部分学生一周平均每天的睡眠时间,结果如下表:
5. 某校为了解学生睡眠情况,随机调查部分学生一周平均每天的睡眠时间,结果如下表:时间/小时
7
8
9
10
人数
6
9
11
4
这些学生睡眠时间的众数、中位数是( )
A、众数是11,中位数是8.5 B、众数是10,中位数是5 C、众数是9,中位数是9 D、众数是9,中位数是8.56. 要组织一次篮球联赛,赛制为单循环形式,每两队之间都赛一场,计划安排15场比赛.设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 x(x﹣1)=15 B、 x(x+1)=15 C、x(x+1)=15 D、x(x﹣1)=157. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,AB CD, , ,则∠AEC的度数为( )
8. 如图,AB CD, , ,则∠AEC的度数为( )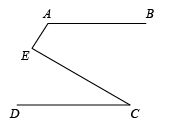 A、 B、 C、 D、9. 如图,矩形 的边长 , .把 绕 逆时针旋转,使 恰好落在 上的点 处,线段 扫过部分为扇形 .则扇形 的面积是( )
A、 B、 C、 D、9. 如图,矩形 的边长 , .把 绕 逆时针旋转,使 恰好落在 上的点 处,线段 扫过部分为扇形 .则扇形 的面积是( ) A、 B、1 C、 D、10. 如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( )
A、 B、1 C、 D、10. 如图,正方形ABCD的边长为5,动点P的运动路线为AB→BC,动点Q的运动路线为BD.点P与Q以相同的速度分别从A,B两点同时出发,当一个点到达终点停止运动时另一个点也随之停止.设点P运动的路程为x,△BPQ的面积为y,则下列能大致表示y与x的函数关系的图象为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 7(毫米2),这个数用科学记数法表示为 .12. 计算: = .13. 如图,平行四边形ABCD的对角线交于点O,过点O的直线EF分别交边AB,CD于E,F两点,在这个平行四边形上做随机投掷图钉试验,针头落在阴影区域内的概率是.
 14. 关于x的一元二次方程 有两个不相等的实数根,则实数m的取值范围是 .15. 某同学5次数学小测验的成绩分别为95分,85分,95分,90分,85分,则该同学这5次成绩的平均数是分.16. 如图, 的一条直角边 在 轴上,双曲线 经过斜边 中点 ,与另一直角边交于点 ,若 ,则 的值为 .
14. 关于x的一元二次方程 有两个不相等的实数根,则实数m的取值范围是 .15. 某同学5次数学小测验的成绩分别为95分,85分,95分,90分,85分,则该同学这5次成绩的平均数是分.16. 如图, 的一条直角边 在 轴上,双曲线 经过斜边 中点 ,与另一直角边交于点 ,若 ,则 的值为 . 17. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,点P是AB边上的一点(异于A,B两点),过点P分别作AC,BC边的垂线,垂足分别为M,N,连接MN,则MN的最小值是 .
17. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,点P是AB边上的一点(异于A,B两点),过点P分别作AC,BC边的垂线,垂足分别为M,N,连接MN,则MN的最小值是 .
三、解答题
-
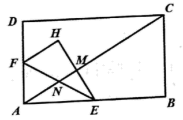
18. 如图,在矩形ABCD中,E是AB的中点,F是为射线AD上的一个动点,将△AEF沿EF折叠得到△HEF,连接AC,分别交EF和直线EH于点N,M,已知∠BAC= , ,若△EMN与△AEF相似,则AF的长为多少?
 19. 先化简,再求值: ,其中 .20. 某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.
19. 先化简,再求值: ,其中 .20. 某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.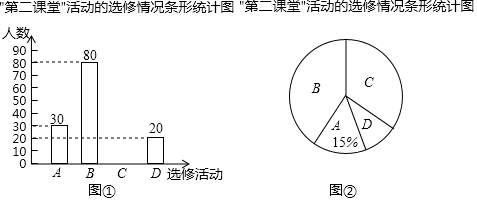
根据图中提供的信息,解答下列问题:
(1)、本次调查的学生共有人;在扇形统计图中,B所对应的扇形的圆心角的度数是;(2)、将条形统计图补充完整;(3)、在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.21. 某快递公司车队现有载重量为8吨、10吨的货车共12辆,全部车辆运输一次可以运输110吨货物.(1)、求该车队有载重量8吨、10吨的货车各多少辆?(2)、随着快递事业的发展,该车队需要一次运输货物不低于180吨,为了能够完成任务,该公司车队准备新购进这两种货车共8辆,则最少购进载重量为10吨的货车多少辆?22. 如图,已知△ABC中,以AB为直径的⊙O交AC于点D,∠CBD=∠A. (1)、求证:BC为⊙O的切线;(2)、若E为 中点,BD=12,sin∠BED= ,求BE的长.23. 在一次海上救援中,两艘专业救助船 同时收到某事故渔船的求救讯息,已知此时救助船 在 的正北方向,事故渔船 在救助船 的北偏西30°方向上,在救助船 的西南方向上,且事故渔船 与救助船 相距120海里.
(1)、求证:BC为⊙O的切线;(2)、若E为 中点,BD=12,sin∠BED= ,求BE的长.23. 在一次海上救援中,两艘专业救助船 同时收到某事故渔船的求救讯息,已知此时救助船 在 的正北方向,事故渔船 在救助船 的北偏西30°方向上,在救助船 的西南方向上,且事故渔船 与救助船 相距120海里.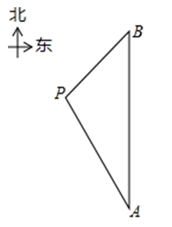 (1)、求收到求救讯息时事故渔船 与救助船 之间的距离;(2)、若救助船A , 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船 处搜救,试通过计算判断哪艘船先到达.24. 为增加农民收入,助力乡村振兴.某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量y(千克)与销售单价x(元/千克)(8≤x≤40)满足的函数图象如图所示.
(1)、求收到求救讯息时事故渔船 与救助船 之间的距离;(2)、若救助船A , 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船 处搜救,试通过计算判断哪艘船先到达.24. 为增加农民收入,助力乡村振兴.某驻村干部指导农户进行草莓种植和销售,已知草莓的种植成本为8元/千克,经市场调查发现,今年五一期间草莓的销售量y(千克)与销售单价x(元/千克)(8≤x≤40)满足的函数图象如图所示.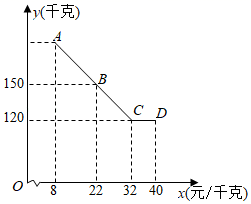 (1)、根据图象信息,求y与x的函数关系式;(2)、求五一期间销售草莓获得的最大利润.25. 如图,在Rt△ABC中, , ,点O为AB中点,点P为直线BC上的动点(不与点B、C重合),连接OC、OP,将线段OP绕点P逆时针旋转 ,得到线段PQ,连接BQ.
(1)、根据图象信息,求y与x的函数关系式;(2)、求五一期间销售草莓获得的最大利润.25. 如图,在Rt△ABC中, , ,点O为AB中点,点P为直线BC上的动点(不与点B、C重合),连接OC、OP,将线段OP绕点P逆时针旋转 ,得到线段PQ,连接BQ. (1)、如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系;(2)、如图2,当点P在CB长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)、如图3,当点P在BC延长线上时,若 , ,请直接写出BQ的长.26. 如图,在平面直角坐标系中,已知抛物线 与x轴交于点A(1,0),B(5,0)两点,与y轴交于点C,点D为抛物线的顶点.
(1)、如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系;(2)、如图2,当点P在CB长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)、如图3,当点P在BC延长线上时,若 , ,请直接写出BQ的长.26. 如图,在平面直角坐标系中,已知抛物线 与x轴交于点A(1,0),B(5,0)两点,与y轴交于点C,点D为抛物线的顶点.
 (1)、求抛物线的解析式和点D的坐标;(2)、求△BCD的面积;(3)、点M为抛物线上一动点,点N为平面内一点,以A,M,I,N为顶点作正方形,是否存在点M,使点I恰好落在对称轴上?若存在,直接写出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式和点D的坐标;(2)、求△BCD的面积;(3)、点M为抛物线上一动点,点N为平面内一点,以A,M,I,N为顶点作正方形,是否存在点M,使点I恰好落在对称轴上?若存在,直接写出点M的坐标;若不存在,请说明理由.