辽宁省本溪市2022年初中毕业练习(一)数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. -0.5的倒数是( )A、-5 B、5 C、-2 D、22. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图所示的几何体是由5个相同的小正方体组成,其主视图为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图所示的几何体是由5个相同的小正方体组成,其主视图为( )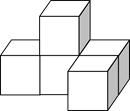 A、
A、 B、
B、 C、
C、 D、
D、 5. 为弘扬传统文化,在端午节前夕,某校举行了“诗词竞赛”,某班10名同学参加了此次竞赛,他们的得分情况如下表所示:
5. 为弘扬传统文化,在端午节前夕,某校举行了“诗词竞赛”,某班10名同学参加了此次竞赛,他们的得分情况如下表所示:人数
1
2
2
3
1
1
成绩(分)
50
60
70
80
90
100
则全班10名同学的成绩的中位数和众数分别是( )
A、75,3 B、70,80 C、75,80 D、80,36. 下列说法正确的是( )A、“买中奖率为 的奖券10张,中奖”是必然事件 B、“汽车累积行驶 ,从未出现故障”是不可能事件 C、某城市气象局预报说“明天的降水概率为70%”,意味着某城市明天一定下雨 D、方差是刻画数据离散程度的量7. 观察下列作图痕迹,所作CD为△ABC的边AB上的中线是( )A、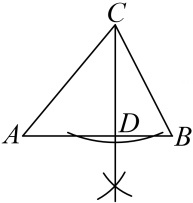 B、
B、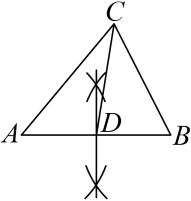 C、
C、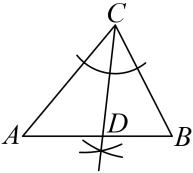 D、
D、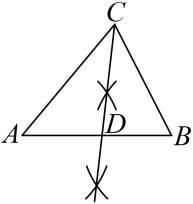 8. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、
8. 在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )A、 B、
B、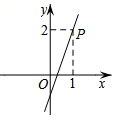 C、
C、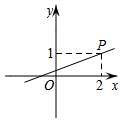 D、
D、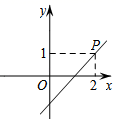 9. 某厂计划加工180万个医用口罩,第一周按原计划的速度生产,一周后以原来速度的1.5倍生产,结果比原计划提前一周完成任务若设原计划每周生产x万个口罩,则可列方程为( )A、 B、 C、 D、10. 如图, , , , ,动点 从 点出发,沿 ,到 点停止运动,点 从点 出发,在 延长线上向右运动,点 、 同时出发,点 停止运动时,点 也停止运动,点 、 的运动速度都是 ,则下列图象能大致反映 的面积 与运动时间 (s)之间函数关系的是( )
9. 某厂计划加工180万个医用口罩,第一周按原计划的速度生产,一周后以原来速度的1.5倍生产,结果比原计划提前一周完成任务若设原计划每周生产x万个口罩,则可列方程为( )A、 B、 C、 D、10. 如图, , , , ,动点 从 点出发,沿 ,到 点停止运动,点 从点 出发,在 延长线上向右运动,点 、 同时出发,点 停止运动时,点 也停止运动,点 、 的运动速度都是 ,则下列图象能大致反映 的面积 与运动时间 (s)之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 今年6月13日是我国第四个文化和自然遗产日.目前,我国世界遗产总数据居世界首位.其中自然遗产总面积约68000 km2 , 将数68000用科学记数法表示应为 .12. 因式分解: .13. 如图,将分别含有 、 角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为 ,则图中角 的度数为.
 14. 关于x的分式方程 的解为正数,则m的取值范围是 .15. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是.
14. 关于x的分式方程 的解为正数,则m的取值范围是 .15. 如图是一张矩形纸板,顺次连接各边中点得到菱形,再顺次连接菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是.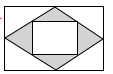 16. 如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG= , 则k=.
16. 如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M,反比例函数y=(x>0)的图象恰好经过点F,M.若直尺的宽CD=3,三角板的斜边FG= , 则k=.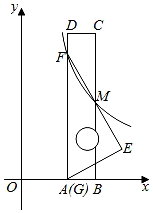 17. 在 中, , , .以 为边作周长为18的矩形 , , 分别为 , 的中点,连接 ,则线段 的长为 .18. 如图,正方形 中,点 是 边上一点,连接 ,以 为对角线作正方形 ,边 与正方形 的对角线 相交于点 ,连接 ,若 ,则 .
17. 在 中, , , .以 为边作周长为18的矩形 , , 分别为 , 的中点,连接 ,则线段 的长为 .18. 如图,正方形 中,点 是 边上一点,连接 ,以 为对角线作正方形 ,边 与正方形 的对角线 相交于点 ,连接 ,若 ,则 .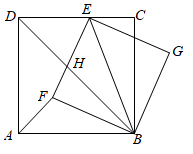
三、解答题
-
19. 先化简,再求值: ,再从 , ,0,1中选择合适的 值代入求值.20. 某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)、两个班共有女生多少人?(2)、将频数分布直方图补充完整;(3)、求扇形统计图中 部分所对应的扇形圆心角度数;(4)、身高在 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.21. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE. (1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.22. 如图,山顶有一塔AB,塔高33m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80m的C处测得A、B的仰角分别为27°、22°,从与F点相距50m的D处测得A的仰角为45°.求隧道EF的长度.(参考数据:tan22°≈0.40,tan27°≈0.51)
(1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.22. 如图,山顶有一塔AB,塔高33m.计划在塔的正下方沿直线CD开通穿山隧道EF.从与E点相距80m的C处测得A、B的仰角分别为27°、22°,从与F点相距50m的D处测得A的仰角为45°.求隧道EF的长度.(参考数据:tan22°≈0.40,tan27°≈0.51)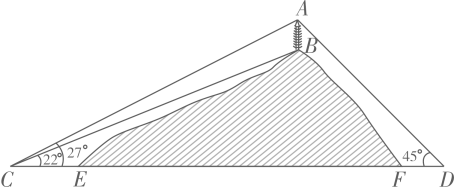 23. 如图, 为 的直径, 是射线 上一点,过点 的直线与 交于 , 两点,与 交于点 ,连接 , ,其中 , , .
23. 如图, 为 的直径, 是射线 上一点,过点 的直线与 交于 , 两点,与 交于点 ,连接 , ,其中 , , . (1)、求证: 为 的切线;(2)、若 , ,求 的直径.24. 2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为 ,销售量y(千克)与x之间的关系如图所示.
(1)、求证: 为 的切线;(2)、若 , ,求 的直径.24. 2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为 ,销售量y(千克)与x之间的关系如图所示. (1)、求y与x之间的函数关系式,并写出x的取值范围;(2)、当月第几天,该农产品的销售额最大,最大销售额是多少?
(1)、求y与x之间的函数关系式,并写出x的取值范围;(2)、当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
25. 如图1, , ,点 , 分别在边 , 上,点 为 中点. (1)、请直接写出线段 与 的关系;(2)、连接 ,将 绕点 逆时针旋转至如图2位置,请写出 与 的关系,并说明理由;(3)、在 绕点 旋转的过程中,当 , , 三点共线时,若 , ,请直接写出 的长.26. 如图,抛物线 交 轴于 、 两点(点 在点 的左侧)坐标分别为 ,交 轴于点 .
(1)、请直接写出线段 与 的关系;(2)、连接 ,将 绕点 逆时针旋转至如图2位置,请写出 与 的关系,并说明理由;(3)、在 绕点 旋转的过程中,当 , , 三点共线时,若 , ,请直接写出 的长.26. 如图,抛物线 交 轴于 、 两点(点 在点 的左侧)坐标分别为 ,交 轴于点 . (1)、求出抛物线解析式:(2)、如图1,过 轴上点 做 的垂线,交线段 于点 ,交抛物线于点 ,当 时,请求出点 的坐标;(3)、如图2,点 的坐标是 ,点 为 轴上一动点,点 在抛物线上,把 沿 翻折,使点 刚好落在 轴上,请直接写出点 的坐标.
(1)、求出抛物线解析式:(2)、如图1,过 轴上点 做 的垂线,交线段 于点 ,交抛物线于点 ,当 时,请求出点 的坐标;(3)、如图2,点 的坐标是 ,点 为 轴上一动点,点 在抛物线上,把 沿 翻折,使点 刚好落在 轴上,请直接写出点 的坐标.