辽宁省鞍山市2022年中考第一次模拟考试数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. ﹣2022的相反数是( )A、﹣2022 B、2022 C、﹣ D、2. 下列立体图形中,主视图、左视图,俯视图都相同的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线a b,直线 分别与 、 相交于 、 两点, 于点 ,交直线 于点 ,已知 ,则 的度数是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线a b,直线 分别与 、 相交于 、 两点, 于点 ,交直线 于点 ,已知 ,则 的度数是( ) A、 B、 C、 D、5. 一个不透明的箱子里装有红色小球和白色小球共4个,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量的重复实验后,发现摸到红色小球的频率稳定于0.75左右.请估计箱子里白色小球的个数是( )A、1 B、2 C、3 D、46. 如图,在平面直角坐标系中, 与 是以原点O为位似中心的位似图形,已知点C的横坐标为1,点F的横坐标为3,点B的坐标为 ,则点E的坐标是( )
A、 B、 C、 D、5. 一个不透明的箱子里装有红色小球和白色小球共4个,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量的重复实验后,发现摸到红色小球的频率稳定于0.75左右.请估计箱子里白色小球的个数是( )A、1 B、2 C、3 D、46. 如图,在平面直角坐标系中, 与 是以原点O为位似中心的位似图形,已知点C的横坐标为1,点F的横坐标为3,点B的坐标为 ,则点E的坐标是( )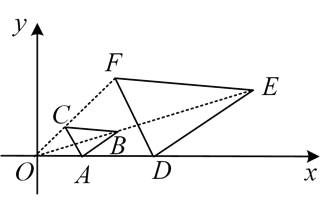 A、 B、 C、 D、7. 如图, ,垂足为D, , , ,则△BCE周长为( )
A、 B、 C、 D、7. 如图, ,垂足为D, , , ,则△BCE周长为( ) A、16 B、17 C、18 D、198. 如图,在平面四边形ABCD中, , ,点M从A出发沿路径 运动,点N从B出发沿路径 运动,M,N两点同时出发,且点N的运动速度是点M运动速度的3倍,当M运动到B时,M,N两点同时停止运动,若M的运动路程为x,△BMN的面积为y;则能反映y与x之间函数关系的图象是( )
A、16 B、17 C、18 D、198. 如图,在平面四边形ABCD中, , ,点M从A出发沿路径 运动,点N从B出发沿路径 运动,M,N两点同时出发,且点N的运动速度是点M运动速度的3倍,当M运动到B时,M,N两点同时停止运动,若M的运动路程为x,△BMN的面积为y;则能反映y与x之间函数关系的图象是( )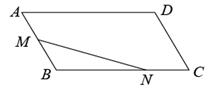 A、
A、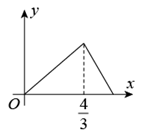 B、
B、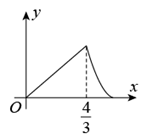 C、
C、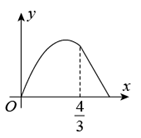 D、
D、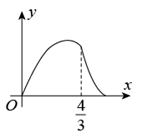
二、填空题
-
9. 分解因式: .10. 如图,在△ABC中, ,将△ABC绕点A逆时针旋转60°得到△AED,AD与BC交于点F,则 的度数为 .
 11. 关于x的一元二次方程 有两个实数根,则k的取值范围是 .12. 如图,△ABC中,点D在边AB上,满足∠ADC=∠ACB,若AC=2,AD=1,则DB= .
11. 关于x的一元二次方程 有两个实数根,则k的取值范围是 .12. 如图,△ABC中,点D在边AB上,满足∠ADC=∠ACB,若AC=2,AD=1,则DB= . 13. 某高科技企业要完成6000个零件的生产任务,按原计划工作一天后,为了尽快完成该项任务,延长了工作时间,之后每天生产的零件数量是原计划的1.5倍,结果提前3天完成任务,求原计划每天生产零件多少个?设原计划每天生产零件x个,则可列方程为 .14. 如图,在 中,半径为4,将三角板的60°、90°角顶点A,B放在圆上,AC,BC两边分别与 交于D,E两点, ,则△ABC的面积为 .
13. 某高科技企业要完成6000个零件的生产任务,按原计划工作一天后,为了尽快完成该项任务,延长了工作时间,之后每天生产的零件数量是原计划的1.5倍,结果提前3天完成任务,求原计划每天生产零件多少个?设原计划每天生产零件x个,则可列方程为 .14. 如图,在 中,半径为4,将三角板的60°、90°角顶点A,B放在圆上,AC,BC两边分别与 交于D,E两点, ,则△ABC的面积为 . 15. 如图,过原点的直线BC与 ( )的图象交于B,C两点,点A在 ( )的图象上,连接AB,AC,且AC与x轴交于点P,若△ABC的面积为6, ,则k的值为 .
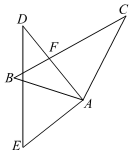
15. 如图,过原点的直线BC与 ( )的图象交于B,C两点,点A在 ( )的图象上,连接AB,AC,且AC与x轴交于点P,若△ABC的面积为6, ,则k的值为 . 16. 如图,在平行四边形ABCD中,AC与BD交于点O,将△ABO沿AC所在的直线翻折得到△AEO,连接ED,EB,且EB分别与AC,AD交于F,H两点, ,则下列结论:① ;② ;③若 ,则 ;④△OED为等边三角形;其中正确的有 . (填序号即可)
16. 如图,在平行四边形ABCD中,AC与BD交于点O,将△ABO沿AC所在的直线翻折得到△AEO,连接ED,EB,且EB分别与AC,AD交于F,H两点, ,则下列结论:① ;② ;③若 ,则 ;④△OED为等边三角形;其中正确的有 . (填序号即可)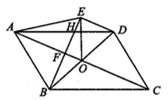
三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图,在平行四边形ABCD中,点E,点F在直线BD上,且 ,连接AF,CE,求证 .
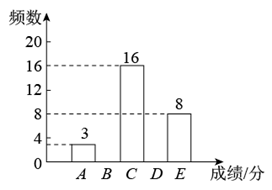
 19. 第二十四届冬奥会于2022年在北京市和张家口市举行,为了调查学生对冬奥知识的了解情况,某校随机抽取部分学生进行了相关知识测试,获得了他们的成绩(满分100分),根据调查结果绘制了不完整的统计图表.根据以下信息,解答下列问题:(1)、这次抽样调查的样本容量为 , a= , b=;(2)、请补全频数统计图;(3)、该校有学生800人,成绩在80分以上(含80分)为优秀,假如全部学生参加此次测试,请估计该校学生成绩为优秀的人数.
19. 第二十四届冬奥会于2022年在北京市和张家口市举行,为了调查学生对冬奥知识的了解情况,某校随机抽取部分学生进行了相关知识测试,获得了他们的成绩(满分100分),根据调查结果绘制了不完整的统计图表.根据以下信息,解答下列问题:(1)、这次抽样调查的样本容量为 , a= , b=;(2)、请补全频数统计图;(3)、该校有学生800人,成绩在80分以上(含80分)为优秀,假如全部学生参加此次测试,请估计该校学生成绩为优秀的人数.组别
成绩分组(单位:分)
频数
频率
A
3
0.06
B
a
0.2
C
16
D
b
E
8
0.16
 20. 小源同学决定利用假期在鞍山本地游玩,鞍山著名景点分别有:A.千山风景区;B.玉佛苑景区;C.汤岗子温泉;D.海城白云山景区.由于受到时间限制,只能选择两个不同),小源同学随机抽两次,每次抽一个签(抽到的签不放回),每个签抽到的机会相等.(1)、小源第一次恰好抽到“玉佛苑景区”的概率是;(2)、请用列表法或画树状图法求出小原同学抽到“汤岗子温泉”和“千山风景区”两个景点中至少一个的概率是多少.21. 某中学数学研究小组在综合实践活动中,组织测量某建筑物AB的高度,下列示意图中B、C、D在同一条直线上,四边形BCEF为矩形,测量方案和数据如表.
20. 小源同学决定利用假期在鞍山本地游玩,鞍山著名景点分别有:A.千山风景区;B.玉佛苑景区;C.汤岗子温泉;D.海城白云山景区.由于受到时间限制,只能选择两个不同),小源同学随机抽两次,每次抽一个签(抽到的签不放回),每个签抽到的机会相等.(1)、小源第一次恰好抽到“玉佛苑景区”的概率是;(2)、请用列表法或画树状图法求出小原同学抽到“汤岗子温泉”和“千山风景区”两个景点中至少一个的概率是多少.21. 某中学数学研究小组在综合实践活动中,组织测量某建筑物AB的高度,下列示意图中B、C、D在同一条直线上,四边形BCEF为矩形,测量方案和数据如表.课题
测量某建筑物的高度
测量工具
测量角度的仪器、皮尺等
测量小组
第一小组
第二小组
第三小组
测量方案示意图
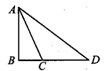


测量数据
米,
,
米
米,
,
请写出你选择的可行的测量方案,并利用数据计算该建筑物的高度.(结果保留整数)
(参考数据: , , , )
22. 如图,正比例函数 的图象和反比例函数 ( )的图象交于点 . (1)、求反比例函数的表达式;(2)、点B为x轴正半轴上一点,连接AB交反比例函数 ( )的图象于点P,若点P恰好为AB中点,求△APO的面积.23. 如图,AB为 直径,点C为 上一点,过O作 ,过C作 分别交AB,DO的延长线于点P,E,若 ;
(1)、求反比例函数的表达式;(2)、点B为x轴正半轴上一点,连接AB交反比例函数 ( )的图象于点P,若点P恰好为AB中点,求△APO的面积.23. 如图,AB为 直径,点C为 上一点,过O作 ,过C作 分别交AB,DO的延长线于点P,E,若 ; (1)、求证:CD为 切线;(2)、若 , ,求 的半径.24. “南果梨”是鞍山市的特产,某水果经销商销售一批南果梨,进价为每千克6元,以每千克10元的价格进行销售,每天可以销售600千克,销售单价每上涨0.5元,则每天销售量减少50千克;若设销售价格为每千克x元 ,每天的销售量为y千克.(1)、求y与x的函数关系式;(2)、当每千克的售价定为多少元时,每天的销售利润最大,最大利润为多少元?25. 如图,在△ABC中, , ,点D为平面内一点,且 ,BD与AC交于点P,过A作 交BD边于点F,
(1)、求证:CD为 切线;(2)、若 , ,求 的半径.24. “南果梨”是鞍山市的特产,某水果经销商销售一批南果梨,进价为每千克6元,以每千克10元的价格进行销售,每天可以销售600千克,销售单价每上涨0.5元,则每天销售量减少50千克;若设销售价格为每千克x元 ,每天的销售量为y千克.(1)、求y与x的函数关系式;(2)、当每千克的售价定为多少元时,每天的销售利润最大,最大利润为多少元?25. 如图,在△ABC中, , ,点D为平面内一点,且 ,BD与AC交于点P,过A作 交BD边于点F, (1)、如图1,过C作 交于E,
(1)、如图1,过C作 交于E,①求证: ;
②求证: ;
(2)、过F作 交AB于H,连接CF,若 , ,求BH的长.26. 如图,抛物线 ( )与x轴正半轴交于点A,点P为线段OA上一点,过P作 轴交抛物线 ( )于点B,过B作 轴交抛物线 ( )于点C,连接AC; (1)、如图1,若点A的横坐标为 ,
(1)、如图1,若点A的横坐标为 ,①求抛物线的解析式;
②当 时,求点P的坐标;
(2)、若 ,点Q为线段AC上一点,点N为x轴上一点,且 ,将△AQP沿直线PQ翻折得到 , 所在的直线交x轴于点M,且 ,求点Q的纵坐标.