江西省赣州市石城县2022年九年级学生数学综合素养试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. (2+1)(22+1)(24+1)…(264+1)﹣1的个位数字是( )A、2 B、4 C、6 D、82. 若实数x,y满足 ,则 的值是( )A、 B、 C、 D、3. 如图,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为( )
 A、 B、 C、 D、4. 如图, 是 的直径, , 是半径 上的一动点, 交 于点 ,在半径 上取点 ,使得 , 交 于点 ,点 位于 两侧,连结 交 于点 .点 从点 出发沿 向终点 运动,在整个运动过程中, 与 的面积和的变化情况是( )
A、 B、 C、 D、4. 如图, 是 的直径, , 是半径 上的一动点, 交 于点 ,在半径 上取点 ,使得 , 交 于点 ,点 位于 两侧,连结 交 于点 .点 从点 出发沿 向终点 运动,在整个运动过程中, 与 的面积和的变化情况是( )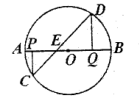 A、一直减小 B、一直不变 C、先变大后变小 D、先变小后变大5. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分 ,反比例函数 的图象经过AE上的两点A,F,且 , 的面积为18,则k的值为( )
A、一直减小 B、一直不变 C、先变大后变小 D、先变小后变大5. 如图,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE.若AD平分 ,反比例函数 的图象经过AE上的两点A,F,且 , 的面积为18,则k的值为( )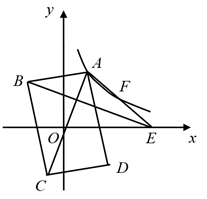 A、6 B、12 C、18 D、246. 若平面直角坐标系内的点 满足横、纵坐标都为整数,则把点 叫做“整点”.例如: 、 都是“整点”.抛物线 与 轴交于A、 两点,若该抛物线在A、 之间的部分与线段 所围成的区域(包括边界)恰有七个整点,则 的取值范围是( )A、 B、 C、 D、
A、6 B、12 C、18 D、246. 若平面直角坐标系内的点 满足横、纵坐标都为整数,则把点 叫做“整点”.例如: 、 都是“整点”.抛物线 与 轴交于A、 两点,若该抛物线在A、 之间的部分与线段 所围成的区域(包括边界)恰有七个整点,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
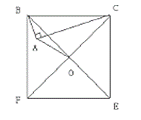
7. 已知 满足 , ,则 .8. 已知正整数x满足 是完全平方数,则x的值是 .9. 如图以直角三角形ABC的斜边BC为边在三角形ABC的同侧作正方形BCEF,设正方形的中心为O,连结AO,如果AB=4,AO=6 ,则AC=
 10. 如图, 是等边三角形,点D为BC边上一点, ,以点D为顶点作正方形DEFG,且 ,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为.
10. 如图, 是等边三角形,点D为BC边上一点, ,以点D为顶点作正方形DEFG,且 ,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为.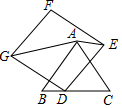 11. 如图 ,邻边长为 和 的矩形分割成①,②,③,④四块后,拼接成如图 不重叠、无缝隙的正方形 ,则图 中 的长为 .
11. 如图 ,邻边长为 和 的矩形分割成①,②,③,④四块后,拼接成如图 不重叠、无缝隙的正方形 ,则图 中 的长为 .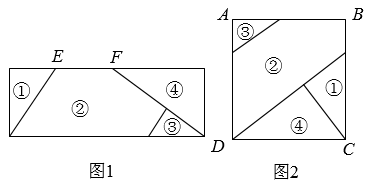 12. 平面直角坐标系中, 交 轴正负半轴于点 、 ,点 为 外 轴正半轴上一点, 为第三象限内 上一点, 交 延长线于点 ,已知 , , ,则 的值为 .
12. 平面直角坐标系中, 交 轴正负半轴于点 、 ,点 为 外 轴正半轴上一点, 为第三象限内 上一点, 交 延长线于点 ,已知 , , ,则 的值为 .
三、解答题
-
13. 已知x1、x2是关于x的方程x2+2x+2k﹣4=0两个实数根,并且x1≠x2 .(1)、求实数k的取值范围;(2)、若k为正整数,且该方程的根都是整数,求k的值;(3)、若|x1﹣x2|=6,求 的值.14. 已知 ,且 ,求证: .15. 正方形ABCD的边长为4,AC,BD交于点E.在点A处建立平面直角坐标系如图所示.
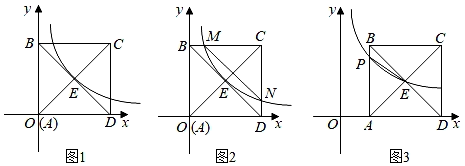 (1)、如图(1),双曲线y= 过点E,完成填空:点C的坐标是 , 点E的坐标是 , 双曲线的解析式是;(2)、如图(2),双曲线y= 与BC,CD分别交于点M,N.求证: ;(3)、如图(3),将正方形ABCD向右平移m(m>0)个单位长度,使过点E的双曲线y= 与AB交于点P.当 AEP为等腰三角形时,求m的值.16. 如图,在 中, ,以 为直径的 分别与 , 交于点 , ,过点 作 ,垂足为点 .
(1)、如图(1),双曲线y= 过点E,完成填空:点C的坐标是 , 点E的坐标是 , 双曲线的解析式是;(2)、如图(2),双曲线y= 与BC,CD分别交于点M,N.求证: ;(3)、如图(3),将正方形ABCD向右平移m(m>0)个单位长度,使过点E的双曲线y= 与AB交于点P.当 AEP为等腰三角形时,求m的值.16. 如图,在 中, ,以 为直径的 分别与 , 交于点 , ,过点 作 ,垂足为点 .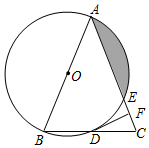 (1)、求证:直线 是 的切线;(2)、求证: ;(3)、若点 是半圆 的一个三等分点,求出阴影部分的面积.17. 如图1,菱形ABCD中,AB=6.∠B=60°,四边形EFGB的顶点E , G分别在边BC和AB上,EF∥CD , FG∥AD , 连接FD .
(1)、求证:直线 是 的切线;(2)、求证: ;(3)、若点 是半圆 的一个三等分点,求出阴影部分的面积.17. 如图1,菱形ABCD中,AB=6.∠B=60°,四边形EFGB的顶点E , G分别在边BC和AB上,EF∥CD , FG∥AD , 连接FD .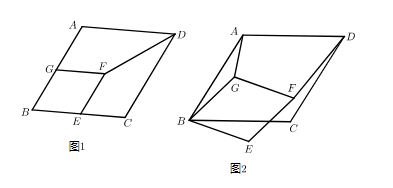 (1)、若DF平分∠ADC , 求证:四边形EFGB为菱形;(2)、在(1)中的条件下,当EC=2时,将四边形EFGB绕点B顺时针旋转至图2所示的位置,连接AG .
(1)、若DF平分∠ADC , 求证:四边形EFGB为菱形;(2)、在(1)中的条件下,当EC=2时,将四边形EFGB绕点B顺时针旋转至图2所示的位置,连接AG .①猜想AG与DF的数量关系,并加以证明;
②当GF过点C时,求sin∠GBC的值.
18. 定义:点 是平面直角坐标系内一点,将函数 的图象位于直线 左侧部分,以直线 为对称轴翻折,得到新的函数 的图象,我们称函数 的函数是函数 的相关函数,函数 的图象记作 ,函数 的图象未翻折的部分记作 ,图象 和 合起来记作图象 .例如:函数 的解析式为 ,当 时,它的相关函数 的解析式为 . (1)、如图,函数 的解析式为 ,当 时,它的相关函数 的解析式为 .(2)、函数 的解析式为 ,当 时,图象 上某点的纵坐标为-2,求该点的横坐标.(3)、已知函数 的解析式为 ,
(1)、如图,函数 的解析式为 ,当 时,它的相关函数 的解析式为 .(2)、函数 的解析式为 ,当 时,图象 上某点的纵坐标为-2,求该点的横坐标.(3)、已知函数 的解析式为 ,①已知点 、 的坐标分别为 、 ,图象 与线段 只有一个公共点时,结合函数图象,求 的取值范围;
②若点 是图象 上任意一点,当 时, 的最小值始终保持不变,求 的取值范围(直接写出结果).