江西省赣州地区2022年九年级中考模拟考数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. 下列四个数中,与﹣2的和为0的数是( )A、﹣2 B、2 C、0 D、﹣2. 下列运算正确的是( )A、3x2+4x2=7x4 B、2x3•3x3=6x3 C、a÷a﹣2=a3 D、(﹣ a2b)3=﹣ a6b33. 如图,一个由圆柱和长方体组成的几何体水平放置,它的俯视图是( )
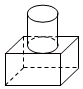 A、
A、 B、
B、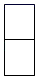 C、
C、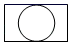 D、
D、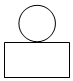 4. 实数 , 在数轴上的位置如图所示,以下说法正确的是( )
4. 实数 , 在数轴上的位置如图所示,以下说法正确的是( ) A、 B、 C、 D、5. 已知锐角∠AOB,如图,
A、 B、 C、 D、5. 已知锐角∠AOB,如图,
⑴在射线OA上取一点C,以点O为圆心,OC长为半径作 , 交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是( )
A、MC=DN B、△COM≌△COD C、若OM=MN.则∠AOB=20° D、MN=3CD6. 已知二次函数 ,当 时, ,则m的取值范围为( ).A、 B、 C、 D、二、填空题
-
7. 江西这片红土圣地,到处传颂着革命先烈可歌可泣的英雄故事.近26万人,这是江西有名有姓的革命烈士的总人数,在烽火连天的峥嵘岁月,他们用鲜血和生命铸就了伟大的井冈山精神、苏区精神、长征精神,孕育了融入民族血脉和灵魂的红色基因.将260000用科学记数法表示为 .8. 不等式组: 的解集是 .9. 已知一组数据4,3,2,m,n的众数为3,平均数为2,m≥n,则n的值为 .10. 已知x1、x2是方程x2﹣mx+2=0的两个根x1=2,则2m﹣5x1•x2= .11. 如图,在菱形ABCD中,对角线AC,BD交于点O,∠ABC=60°,AB=2,分别以点A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为.(结果保留π)

12. 如图,在▱ABCD中,已知AD=10cm,tanB=2,AE⊥BC于点E,且AE=4cm,点P是BC边上一动点.若△PAD为直角三角形,则BP的长为
三、解答题
-
13.(1)、计算:|﹣ |+(4﹣π)0﹣2sin60°+( )﹣1 .(2)、已知正六边形ABCDEF的中心为O,半径OA=6.
①求正六边形ABCDEF的边长;
②以A为圆心,AF为半径画弧BF,求弧BF的长.(结果保留π)
 14. 先化简,再求值: ,其中 .15. 如图,矩形OABC与⊙O交于点D,点A为⊙O上一点,AB=3BC,请仅用无刻度的直尺,分别按下列要求作图(保留作图痕迹).
14. 先化简,再求值: ,其中 .15. 如图,矩形OABC与⊙O交于点D,点A为⊙O上一点,AB=3BC,请仅用无刻度的直尺,分别按下列要求作图(保留作图痕迹).

图1 图2
(1)、若E、F分别OC、AB是的一个三等分点,请在图1中作出过点D的切线;(2)、在图2中作一个圆周角,使这个角的正切值为 .16. 2022年冬奥会吉祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”,如图,现有三张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中两张正面印有冰墩墩图案的卡片分别记为A1、A2 , 正面印有雪容融图案的卡片记为B,将三张卡片正面向下洗匀,小明同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片. (1)、从这三张卡片中随机挑选一张,是“雪容融”的是 事件(填“必然”“随机”或“不可能”);(2)、请用画树状图或列表的方法,求小明同学抽出的两张卡片都是冰墩墩卡片的概率.17.(1)、问题解决
(1)、从这三张卡片中随机挑选一张,是“雪容融”的是 事件(填“必然”“随机”或“不可能”);(2)、请用画树状图或列表的方法,求小明同学抽出的两张卡片都是冰墩墩卡片的概率.17.(1)、问题解决糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个?
 (2)、反思归纳
(2)、反思归纳现有 根竹签, 个山楂.若每根竹签串 个山楂,还剩余 个山楂,则下列等式成立的是 ▲ (填写序号).
⑴ ;⑵ ;⑶ .
18. 某校开展课后延时服务,计划组织学生参加“书法”、“摄影”、“航模、“围棋”四个课外兴趣小组,由于师资等条件的限制,每人只能选择其中一个小组,为了解学生对四个课外兴趣小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出),请你根据给出的信息解答下列问题: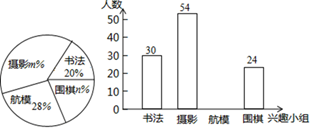 (1)、求参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);(2)、m= , n=;(3)、求扇形统计图中,“摄影”对应扇形圆心角的度数;(4)、若该校共有1200名学生参加课后延时服务,试估计该校选择“围棋”课外兴趣小组的学生有多少人?19. 如图:直线y=x与反比例函数y= (k>0)的图象在第一象限内交于点A(2,m).
(1)、求参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);(2)、m= , n=;(3)、求扇形统计图中,“摄影”对应扇形圆心角的度数;(4)、若该校共有1200名学生参加课后延时服务,试估计该校选择“围棋”课外兴趣小组的学生有多少人?19. 如图:直线y=x与反比例函数y= (k>0)的图象在第一象限内交于点A(2,m).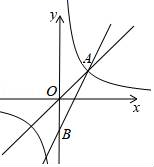 (1)、求m、k的值;(2)、点B在y轴负半轴上,若△AOB的面积为2,求AB所在直线的函数表达式;(3)、将△AOB沿直线AB向上平移,平移后A、O、B的对应点分别为A'、O'、B',当点O'恰好落在反比例函数y= 的图象上时,求点A'的坐标.20. 如图1是某工厂生产的某种多功能儿童车,根据需要可变形为滑板车或三轮车,图2,图3是其示意图,已知前后车轮半径相同,车杆AB的长为60cm,点D是AB的中点,前支撑板DE=30cm,后支撑板EC=40cm,车杆AB与BC所成的∠ABC=53°.(参考数据: )
(1)、求m、k的值;(2)、点B在y轴负半轴上,若△AOB的面积为2,求AB所在直线的函数表达式;(3)、将△AOB沿直线AB向上平移,平移后A、O、B的对应点分别为A'、O'、B',当点O'恰好落在反比例函数y= 的图象上时,求点A'的坐标.20. 如图1是某工厂生产的某种多功能儿童车,根据需要可变形为滑板车或三轮车,图2,图3是其示意图,已知前后车轮半径相同,车杆AB的长为60cm,点D是AB的中点,前支撑板DE=30cm,后支撑板EC=40cm,车杆AB与BC所成的∠ABC=53°.(参考数据: ) (1)、如图2,当支撑点E在水平线BC上时,求支撑点E与前轮轴心B之间的距离BE的长;(2)、如图3,当座板DE与地平面保持平行时,问变形前后两轴心BC的长度有没有发生变化?若不变,请通过计算说明;若变化,请求出变化量.21. 已知,AB是⊙O的直径,C是⊙O上半圆弧上一动点,D是 的中点,弦AC与弦BD交于点E.过点C作⊙O的切线CF交射线AB于点F.
(1)、如图2,当支撑点E在水平线BC上时,求支撑点E与前轮轴心B之间的距离BE的长;(2)、如图3,当座板DE与地平面保持平行时,问变形前后两轴心BC的长度有没有发生变化?若不变,请通过计算说明;若变化,请求出变化量.21. 已知,AB是⊙O的直径,C是⊙O上半圆弧上一动点,D是 的中点,弦AC与弦BD交于点E.过点C作⊙O的切线CF交射线AB于点F.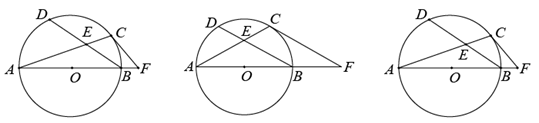
图1 图2 图3
(1)、如图1.当∠AFC=50°时,求∠ABD的度数.(2)、如图2,CF//DB,求∠AFC的度数.(3)、如图3,连接BC,E是BD的中点,已知AB=6,求BC的长和△CBF的面积.22. 如图,二次函数y=ax2+bx﹣3(x≤3)的图象过点A(﹣1,0),B(3,0),C(0,c),记为L.将L沿直线x=3翻折得到“部分抛物线”K,点A,C的对应点分别为点A',C'. (1)、求a,b,c的值;(2)、画出“部分抛物线”K的图象,并求出它的解析式;(3)、某同学把L和“部分抛物线”K看作一个整体,记为图形“W”,若直线y=m和图形“W”只有两个交点M,N(点M在点N的左侧).
(1)、求a,b,c的值;(2)、画出“部分抛物线”K的图象,并求出它的解析式;(3)、某同学把L和“部分抛物线”K看作一个整体,记为图形“W”,若直线y=m和图形“W”只有两个交点M,N(点M在点N的左侧).①直接写出m的取值范围;
②若△MNB为等腰直角三角形,求m的值.
23. 我们定义:有一组邻角相等的凸四边形做“等邻角四边形”,例如:如图1,∠B=∠C,则四边形ABCD为等邻角四边形.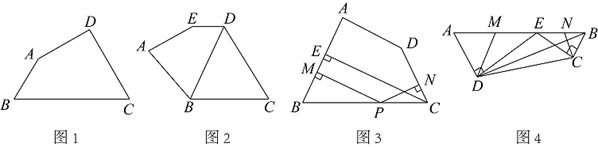 (1)、定义理解:已知四边形ABCD为等邻角四边形,且∠A=130°,∠B=120°,则∠D=度.(2)、变式应用:如图2,在五边形ABCDE中,ED∥BC,对角线BD平分∠ABC.
(1)、定义理解:已知四边形ABCD为等邻角四边形,且∠A=130°,∠B=120°,则∠D=度.(2)、变式应用:如图2,在五边形ABCDE中,ED∥BC,对角线BD平分∠ABC.①求证:四边形ABDE为等邻角四边形;
②若∠A+∠C+∠E=300°,∠BDC=∠C,请判断△BCD的形状,并明理由.
(3)、深入探究:如图3,在等邻角四边形ABCD中,∠B=∠BCD,CE⊥AB,垂足为E,点P为边BC上的一动点,过点P作PM⊥AB,PN⊥CD,垂足分别为M,N.在点P的运动过程中,判断PM+PN与CE的数量关系?请说明理由.(4)、迁移拓展:如图4,是一个航模的截面示意图.四边形ABCD是等邻角四边形,∠A=∠ABC,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,AB=2 dm,AD=3dm,BD= dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.