黑龙江省哈尔滨市巴彦县2022年九年级中考二模数学试题

试卷更新日期：2022-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的倒数是（）

A、 $3$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、-3

查看试题解析
2. 下列运算正确的是（）

A、 ${(a^{2})}^{5} = a^{7}$ B、 $a^{2} \cdot a^{4} = a^{6}$ C、 $3 a^{2} b - 3 a b^{2} = 0$ D、 $（ \frac{a}{2} ）^{2} = \frac{a^{2}}{2}$

查看试题解析
3. 在下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4.
由4个相同的小立方体搭成的几何体如图所示，则它的主视图是（　　）

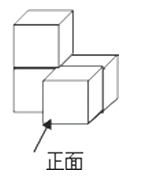A、 B、 C、 D、

查看试题解析
5. 如图， $C D$ 为 $⊙ O$ 的直径，过点D的弦 $D E$ 平行于半径 $O A$ ，若 $∠ A$ 的度数是 $25 °$ ，则 $∠ D$ 的度数为（）

A、 $25 °$ B、 $30 °$ C、 $40 °$ D、 $50 °$

查看试题解析
6. 将二次函数 $y = x^{2}$ 的图象向右平移3个单位，再向上平移1个单位后，所得图象的函数表达式是（）

A、 $y = {(x + 3)}^{2} + 1$ B、 $y = {(x - 3)}^{2} + 1$ C、 $y = {(x - 3)}^{2} - 1$ D、 $y = {(x + 3)}^{2} - 1$

查看试题解析
7. 一款手机连续两次降价，由原来的2298元降到1680元，设平均每次降价的百分率为x，则列方程为（）

A、 $1680 {(1 + x)}^{2} = 2298$ B、 $2298 {(1 + x)}^{2} = 1680$ C、 $1680 {(1 - x)}^{2} = 2298$ D、 $2298 {(1 - x)}^{2} = 1680$

查看试题解析
8. 分式方程 $\frac{100}{20 + x} = \frac{60}{20 - x}$ 的解是（）

A、 $x = - 20$ B、 $x = 5$ C、 $x = - 5$ D、 $x = 20$

查看试题解析
9. 反比例函数 $y = \frac{a + 3}{x}$ 的图象与直线 $y = - x$ 有交点，则a的取值范围是（）

A、 $a \geq - 3$ B、 $a > - 3$ C、 $a \leq - 3$ D、 $a < - 3$

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中，点E是 $A B$ 上任意一点，过点E作 $E F ∥ B C$ 交 $C D$ 于点F，连接 $A F$ 并延长交 $B C$ 的延长线于点H，则下列结论中正确的是（）

A、 $\frac{C F}{A E} = \frac{F H}{A H}$ B、 $\frac{A E}{B E} = \frac{C H}{E F}$ C、 $\frac{A D}{B H} = \frac{A E}{B E}$ D、 $\frac{B E}{C D} = \frac{F H}{A H}$

查看试题解析

二、填空题

11. 将数字2022000用科学记数法可表示为．

查看试题解析
12. 在函数 $y = \frac{1}{2 x + 3}$ 中，自变量x的取值范固是．

查看试题解析
13. 分解因式：2ab²+4ab+2a= ．

查看试题解析
14. 不等式组 ${\begin{matrix} x - 2 > - 3 \\ 3 - x \leq 1 \end{matrix}$ 的解集是．

查看试题解析
15. 二次函数 $y = - {(x - 1)}^{2} + 2$ 的图像与y轴交点坐标是．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ A B C = 90 ° ， A B = 3 ， A C = 6$ ，将 $△ A B C$ 绕点C按逆时针方向旋转得到 $△ A_{1} B_{1} C$ ，使 $C B_{1} ∥ A D$ ，分别延长 $A B$ 、 $C A_{1}$ 相交于点D，则线段 $B D$ 的长为．

查看试题解析
17. 已知扇形的面积为15πcm² ，弧长为5πcm，则该扇形的圆心角是度．

查看试题解析
18. 在 $△ A B C$ 中， $∠ A = 110 °$ ，点D在 $△ A B C$ 内，将射线 $B A$ 沿直线 $B D$ 翻折，将射线 $C A$ 沿直线 $C D$ 翻折，两射线交于点E，若 $∠ B E C = 150 °$ ，则 $∠ B D C$ 的度数为．

查看试题解析
19. 不透明的袋中装有1个红球，2个白球，1个黑球，它们除颜色外完全相同，从袋中任意摸出一个球再放回，再摸出一个球，两次摸出的都是白球的概率是．

查看试题解析
20. 已知，如图所示， $Δ A B C$ 中， $A B = A C$ ， $A D / / B C$ ，且 $B D = 7$ ， $C D = 3$ ， $∠ A C D = 60 °$ ，则线段 $A D$ 的长为．

查看试题解析

三、解答题

21. 先化简，再求值 $(1 + \frac{1}{x - 2}) \div \frac{x^{2} - 1}{2 x - 4}$ ，其中x＝2sin60°－tan45°

查看试题解析
22. 如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A、B、C、D均在小正方形的顶点上．

(1)、在方格纸中画以AB为一边的正方形ABEF，点E、F均在小正方形的顶点上；

(2)、在方格纸中画以CD为一边的菱形CDGH，点G、H均在小正方形的顶点上，且菱形的面积为15，连接EG，并直接写出线段EG的长．

查看试题解析
23. 某中学为了了解学生参加体育活动的情况，对学生进行了随机抽样调查，按每天参加体育活动时间的多少将调查学生分为A、B、C、D四组，A、B两组人数的比为 $3 ： 5$ ，绘制成统计图如图所示，请结合统计图回答下列问题：

(1)、在这次调查中，一共抽取了多少名学生？

(2)、将B组图形补充完整；

(3)、若C组参加体育活动时间为合格，你估计全校3000名学生中，每天参加体育活动时间合格（不包括优良）的学生约有多少名？

查看试题解析
24. 如图， $A B = B D$ ， $A C = C D$ ， $A D$ 平分 $∠ B A C$ ， $A D$ 交 $B C$ 于点O．

(1)、如图1，求证：四边形 $A B D C$ 是菱形；

(2)、如图2，点E为 $B D$ 边的中点，连接 $A E$ 交 $B C$ 于点F，若 $2 ∠ F A O = ∠ A C D$ ，在不添加任何辅助线和字母的条件下，请直接写出图2中所有面积是 $△ A B F$ 面积的整数倍的三角形．

查看试题解析
25. 某商店欲购进A、B两种商品，若购进A种商品5件和B种商品4件需300元；若购进A种商品6件和B种商品8件需440元．

(1)、求A、B两种商品每件的进价分别为多少元？

(2)、商店准备用不超过1615元购进50件这两种商品，求购进A种商品最多是多少件？

查看试题解析
26. 如图，在 $⊙ O$ 中，点A、B、C在 $⊙ O$ 上，射线 $A O$ 交 $B C$ 于点H，弧 $A B =$ 弧 $A C$ ．

(1)、求证 $B H = C H$ ；

(2)、如图，延长 $A H$ 交 $⊙ O$ 于点D，E为 $⊙ O$ 上一点，且弧 $C E =$ 弧 $C D$ ，点F在 $A B$ 上， $F G ⊥ A E$ 于点G， $C K ⊥ A E$ 于点K，若 $F G = B C$ ，求证： $C K = \frac{1}{2} F G$ ；

(3)、在（2）的条件下，连接 $CO$ 并延长交 $F G$ 于点W，若 $A B = 2 C E$ ， $F C = G C$ ， $W G = 33$ ，求 $O W$ 的长．

查看试题解析
27. 已知：抛物线 $y = - x^{2} + b x + c$ 与x轴交点 $A (- 1 ， 0)$ 和点 $B (3 ， 0)$ ，与y轴交于点C．

(1)、求抛物线的解析式；

(2)、P为直线 $B C$ 上方抛物线上一点，过点P作 $P H ⊥ x$ 轴于点H，交 $B C$ 于点D，连接 $P C$ 、 $P B$ ，设 $△ P B C$ 的面积为S，点P的横坐标为t，求S与t的函数关系式，并直接写出自变量t的取值范围；

(3)、如图在（2）的条件下，在线段 $O C$ 上取点M，使 $C M = 2 D H$ ，在第一象限的抛物线上取点N，连接 $D M$ 、 $D N$ ，过点M作 $M G ⊥ D N$ 交直线 $P D$ 于点G，连接 $N G$ ， $∠ M D C = ∠ N D G$ ， $∠ C M G = ∠ N G M$ ，求线段 $N G$ 的长．

查看试题解析