河北省张家口市2022年中考一模数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. 如图,对于四条线段a,b,c,d,请借助直尺或圆规判断长度最大的为( )
 A、a B、b C、c D、d2. 计算: ( )A、-8 B、8 C、7 D、-93. 如图, ,点D在 上, ,则 ( )
A、a B、b C、c D、d2. 计算: ( )A、-8 B、8 C、7 D、-93. 如图, ,点D在 上, ,则 ( ) A、 B、 C、 D、不能确定4. 已知a为实数,则下列各式的值不可能等于1的为( )A、 B、 C、 D、5. 如图,是由3个相同的正方体组成的一个立体图形,则它的俯视图为( )
A、 B、 C、 D、不能确定4. 已知a为实数,则下列各式的值不可能等于1的为( )A、 B、 C、 D、5. 如图,是由3个相同的正方体组成的一个立体图形,则它的俯视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 若 ,则 的值为( )A、18 B、-18 C、6 D、-67. 如图,在4×4的正方形网格中,△ABC的顶点均在格点上,边AB,BC分别与网格线交于点D,E,连接AE,CD交于点F,则点F为△ABC的( )
6. 若 ,则 的值为( )A、18 B、-18 C、6 D、-67. 如图,在4×4的正方形网格中,△ABC的顶点均在格点上,边AB,BC分别与网格线交于点D,E,连接AE,CD交于点F,则点F为△ABC的( )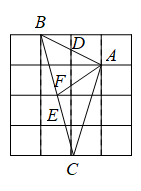 A、内心 B、外心 C、重心 D、中心8. 已知1纳米 米,将 纳米用科学记数法表示为 米的形式,则a,n的值分别为( )A、2.5,-10 B、2.5,-9 C、2.5,-8 D、4,-109. 一班、二班各有m名学生,某次体能测试后,对测试成绩进行了整理和分析(成绩用x表示,单位:分),分成四个组:甲: ;乙: ;丙: ;丁: ,并绘制了下列统计图:
A、内心 B、外心 C、重心 D、中心8. 已知1纳米 米,将 纳米用科学记数法表示为 米的形式,则a,n的值分别为( )A、2.5,-10 B、2.5,-9 C、2.5,-8 D、4,-109. 一班、二班各有m名学生,某次体能测试后,对测试成绩进行了整理和分析(成绩用x表示,单位:分),分成四个组:甲: ;乙: ;丙: ;丁: ,并绘制了下列统计图:
已知一班在乙组中共有15名同学,他们的成绩分别为:
85,85,85,86,87,87,87,87,88,88,88,89,89,88,88.
根据以上信息,下列结论正确的为( )
A、 B、 C、二班成绩的众数在乙组 D、一班成绩的中位数为87分10. 若不等式组 的最大整数解与最小整数解的差为3,则m的值可能为( )A、8 B、10 C、11 D、1311. 如图, 中, ,点E为 的中点.按以下步骤作图:①以点E为圆心、任意长为半径画弧,交 于点M,N;②分别以点M,N为圆心、大于 的长为半径画弧,两弧交于点P;③作射线 交 于点F,连接 .
则 ( )
 A、 B、 C、 D、12. 若关于x的一元二次方程 (n为整数)有两个不相等的实数根,则n的最小值为( )A、0 B、1 C、-1 D、-213. 如图, 是半圆O的直径,点C,D,E依次是半圆上的三点,若 ,则 的度数为( )
A、 B、 C、 D、12. 若关于x的一元二次方程 (n为整数)有两个不相等的实数根,则n的最小值为( )A、0 B、1 C、-1 D、-213. 如图, 是半圆O的直径,点C,D,E依次是半圆上的三点,若 ,则 的度数为( )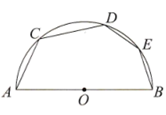 A、 B、 C、 D、14. 对于点 和直线 ,下列说法正确的是( )A、若 ,则l经过点P B、若 ,则l不经过点P C、若 ,则点P在l上方 D、若 ,则点P在l下方15. 如图,平行线m,n间的距离为5,直线l与m,n分别交于点A,B, ,在m上取点P(不与点A重合),作点P关于l的对称点Q.若 ,则点Q到n的距离为( )
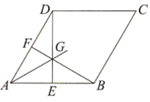
A、 B、 C、 D、14. 对于点 和直线 ,下列说法正确的是( )A、若 ,则l经过点P B、若 ,则l不经过点P C、若 ,则点P在l上方 D、若 ,则点P在l下方15. 如图,平行线m,n间的距离为5,直线l与m,n分别交于点A,B, ,在m上取点P(不与点A重合),作点P关于l的对称点Q.若 ,则点Q到n的距离为( ) A、2 B、3 C、2或8 D、3或816. 如图,在边长为 的菱形 中, ,点E,F分别为折线 上的点(不含菱形顶点), , 、 相交于点G,作射线 .甲、乙二人分别对这个问题进行了研究:
A、2 B、3 C、2或8 D、3或816. 如图,在边长为 的菱形 中, ,点E,F分别为折线 上的点(不含菱形顶点), , 、 相交于点G,作射线 .甲、乙二人分别对这个问题进行了研究:甲:射线 不一定经过点C;
乙:当 垂直于菱形的边时,线段 的长可能为3.
下列判断正确的为( )
 A、甲、乙都对 B、甲、乙都错 C、甲对,乙错 D、甲错,乙对
A、甲、乙都对 B、甲、乙都错 C、甲对,乙错 D、甲错,乙对二、填空题
-
17. 计算: .18. 大、小两个正方形按图方式放置,反比例函数 的图象经过小正方形的一个顶点A,且与大正方形的一边交于点 .
 (1)、k=;(2)、图中阴影部分的面积为 .19. 如图1,五边形ABCDE中,BC=CD=DE=6,∠C=∠D=120°.小明针对图形特点,对这个图形进行了补充和研究:
(1)、k=;(2)、图中阴影部分的面积为 .19. 如图1,五边形ABCDE中,BC=CD=DE=6,∠C=∠D=120°.小明针对图形特点,对这个图形进行了补充和研究: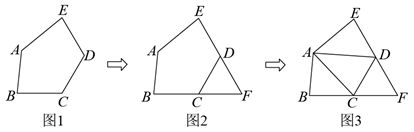 (1)、分别延长BC,ED相交于点F,得到图2,则∠F= ;(2)、再连接AC,AD,得到图3,若S△ABC=10 ,S△ADE=12 ,则S△ACD= .
(1)、分别延长BC,ED相交于点F,得到图2,则∠F= ;(2)、再连接AC,AD,得到图3,若S△ABC=10 ,S△ADE=12 ,则S△ACD= .三、解答题
-
20. 如图,数轴上点A在原点的左侧,到原点的距离为3个单位长度,点B在点A的右侧,与点A的距离为5个单位长度.点A,B对应的数分别为a,b.
 (1)、求 ;(2)、点C也是数轴上的点,它对应的数为x,若点C与点A的距离不小于5,求x的取值范围.21. 现有质量分数分别为8%和13%的两种盐水.常温下,从这两种盐水中各取一部分,混合制成另一种盐水.(1)、若从8%和13%的两种盐水中分别取 ,求混合制成盐水的质量分数(用含a,b的式子表示);(2)、要混合制成 质量分数为10%的盐水,需要取用8%和13%的两种盐水各多少千克?22. 某商店经营某种常用易耗品,为了预测未来1周这种易耗品的销售情况,该商店对近4周每天的销售量(单位:件)进行了统计,并绘制了条形统计图,如图.
(1)、求 ;(2)、点C也是数轴上的点,它对应的数为x,若点C与点A的距离不小于5,求x的取值范围.21. 现有质量分数分别为8%和13%的两种盐水.常温下,从这两种盐水中各取一部分,混合制成另一种盐水.(1)、若从8%和13%的两种盐水中分别取 ,求混合制成盐水的质量分数(用含a,b的式子表示);(2)、要混合制成 质量分数为10%的盐水,需要取用8%和13%的两种盐水各多少千克?22. 某商店经营某种常用易耗品,为了预测未来1周这种易耗品的销售情况,该商店对近4周每天的销售量(单位:件)进行了统计,并绘制了条形统计图,如图. (1)、求这4周平均每天的销售量;(2)、若除用户的日常消耗外,销售量不受其他因素影响,结合近4周的销售数据解决问题:
(1)、求这4周平均每天的销售量;(2)、若除用户的日常消耗外,销售量不受其他因素影响,结合近4周的销售数据解决问题:①估计未来1周某一天的销售量多于25件的概率;
②已知这种易耗品的进价为每件12元,售价为每件18元,估计未来1周销售这种易耗品的利润.
23. 如图, ,射线 ,点P为 上一点,以 为直径作 ,点D在 上, ,连接 ,点Q为弦 上一点,射线 交 于点E. (1)、求证: 为 的切线;(2)、若 ,求:
(1)、求证: 为 的切线;(2)、若 ,求:①劣弧 的长;
② 长的取值范围.
24. 小明从家里出发,去往离家 的某基地,首先步行 走了 ,然后骑共享自行车行 到达基地,参加了 的实践活动后,骑共享自行车按原来的骑行速度原路返回家里,下图反映了在这个过程中小明与家的距离 与离开家的时间 之间的对应关系.
请根据相关信息,解答下列问题:
(1)、求小明从离开基地到返回家里所用的时间;(2)、若 ,求线段 所在直线的解析式;(3)、在小明返回家里的过程中,当小明离开家 时,他与家的距离可能小于 吗?请通过计算说明理由.25. 如图,矩形 中, ,点P,Q分别在 上(均不含端点),且 点E,将 平移得到 ,点P与点Q对应,设 . (1)、计算 ▲ ;当 时,求 的长,(2)、尝试①若 ,求x的值;
(1)、计算 ▲ ;当 时,求 的长,(2)、尝试①若 ,求x的值;②当 时,求点F到 的距离(用含x的式子表示).
(3)、探究连接 ,若点P为 的中点,直接写出 的长.26. 直线: 与抛物线 相交于点A,B,与y轴相交于点C,点 在L上且位于点A,B之间, 轴交l于点Q. (1)、小静得出结论:l与L有一个公共点在x轴上,请判断小静的结论是否正确,并说明理由.(2)、若 ,如图1.
(1)、小静得出结论:l与L有一个公共点在x轴上,请判断小静的结论是否正确,并说明理由.(2)、若 ,如图1.①当 时,求点Q的坐标;
②当m为何值时, 的面积最大?并求出这个最大值.
(3)、若n随m的增大而增大,直接写出a的取值范围.