广州市从化区2022年九年级下学期数学一模试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. 实数4的倒数是( )A、±2 B、2 C、 D、-42. 下列计算正确的是( )A、 =-4 B、(a2)3=a5 C、2a-a=2 D、a•a3=a43. 下列图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 截至2021年2月3日,由中国空间技术研究院研制的“天问一号”探测器飞行里程已超过450000000公里,将数据450000000用科学记数法表示为( )A、45×107 B、4.5×107 C、4.5×108 D、0.45×1095. 某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数分别为6 , 10 , 5 , 3 , 4 , 8 , 4 ,这组数据的中位数和极差分别是()
4. 截至2021年2月3日,由中国空间技术研究院研制的“天问一号”探测器飞行里程已超过450000000公里,将数据450000000用科学记数法表示为( )A、45×107 B、4.5×107 C、4.5×108 D、0.45×1095. 某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数分别为6 , 10 , 5 , 3 , 4 , 8 , 4 ,这组数据的中位数和极差分别是()
A、4, 7 B、5, 7 C、7, 5 D、3, 76. 方程 的解为( )A、x=4 B、x= C、x= D、x=7. 如图,将 ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则∠A的正切值是( ) A、 B、 C、2 D、8. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD交AD于点E,AB=6,BC=10,则EF长为( )
A、 B、 C、2 D、8. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD交AD于点E,AB=6,BC=10,则EF长为( )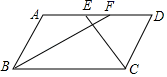 A、1 B、2 C、3 D、49. 如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为﹣1,则一次函数y=(a﹣b)x+b的图象大致是( )
A、1 B、2 C、3 D、49. 如图,二次函数y=ax2+bx的图象开口向下,且经过第三象限的点P.若点P的横坐标为﹣1,则一次函数y=(a﹣b)x+b的图象大致是( )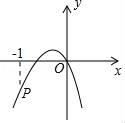 A、
A、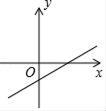 B、
B、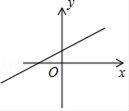 C、
C、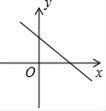 D、
D、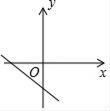 10. 符号“f”表示一种运算,它对一些数的运算结果如下:
10. 符号“f”表示一种运算,它对一些数的运算结果如下:⑴f(1)=2,f(2)=4,f(3)=6…;(2)f( )=2,f( )=3,f( )=4….利用以上规律计算:f(2022)﹣f( )等于( )
A、2021 B、2022 C、 D、二、填空题
-
11. 分解因式: -9= .12. 函数y= 中,自变量x的取值范围是.13. 在△ABC中,已知D、E分别为边AB、AC的中点,若△ADE的周长为4cm,则△ABC的周长为cm .14. 若圆锥底面圆的直径和母线长均为4cm,则它的侧面展开图的面积等于 cm2 .15. 已知二次函数y=﹣x2+bx+c的顶点为(1,5),那么关于x的一元二次方程﹣x2+bx+c﹣m=0有两个相等的实数根,则m= .16. 如图,在Rt△ABC中,∠BAC=90°,AB=AC,点P是AB边上一动点,作PD⊥BC于点D,线段AD上存在一点Q,当QA+QB+QC的值取得最小值,且AQ=2时,则PD= .

三、解答题
-
17. 解不等式组: ,并把解集在数轴上表示出来.
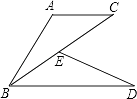
 18. 已知:如图,E为BC上一点,AC∥BD,AC=BE,BC=BD.
18. 已知:如图,E为BC上一点,AC∥BD,AC=BE,BC=BD.求证:AB=DE.
 19. 已知 .(1)、化简A;(2)、当 ,求A的值.20. 根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔.某日我市交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:
19. 已知 .(1)、化简A;(2)、当 ,求A的值.20. 根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔.某日我市交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:年龄x(岁)
人数
男性占比
x<20
4
75%
20≤x<30
m
60%
30≤x<40
25
60%
40≤x<50
8
75%
x≥50
3
100%
(1)、统计表中 的值为;(2)、在这50人中男性所占百分率是 ;(3)、若从年龄在“x<20”的4人中随机抽取2人参加交通安全知识学习,求恰好抽到一男一女的概率.(请用列表或画树状图的方法)21. 2022年北京冬奥会吉祥物“冰墩墩”意喻敦厚、健康、活泼、可爱,象征着冬奥会运动员强壮的身体、坚韧的意志和鼓舞人心的奥林匹克精神.随着北京冬奥会开幕日的临近,某特许零售店“冰墩墩”的销售日益火爆.据统计,该店2021年10月的销量为3万件,2021年12月的销量为3.63万件. (1)、求该店“冰墩墩”销量的月平均增长率;(2)、假设该店“冰墩墩”销量的月平均增长率保持不变,则2022年1月“冰墩墩”的销量有没有超过4万件?请利用计算说明.22. 如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A的坐标为(3,4).
(1)、求该店“冰墩墩”销量的月平均增长率;(2)、假设该店“冰墩墩”销量的月平均增长率保持不变,则2022年1月“冰墩墩”的销量有没有超过4万件?请利用计算说明.22. 如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A的坐标为(3,4). (1)、求过点B的反比例函数y= 的解析式;(2)、连接OB,过点B作BD⊥OB交x轴于点D,求直线BD的解析式.23. 已知,如图,在Rt△ABC中,∠C=90°,AD平分∠CAB.
(1)、求过点B的反比例函数y= 的解析式;(2)、连接OB,过点B作BD⊥OB交x轴于点D,求直线BD的解析式.23. 已知,如图,在Rt△ABC中,∠C=90°,AD平分∠CAB. (1)、按要求尺规作图:作AD的垂直平分线(保留作图痕迹);(2)、若AD的垂直平分线与AB相交于点O,以O为圆心作圆,使得圆O经过AD两点.
(1)、按要求尺规作图:作AD的垂直平分线(保留作图痕迹);(2)、若AD的垂直平分线与AB相交于点O,以O为圆心作圆,使得圆O经过AD两点.①求证:BC是⊙O的切线;②若 ,求⊙O的半径.
24. 在平面直角坐标系中,O为坐标原点,二次函数y= x2﹣2x+a2﹣1(a≠0,且a为常数)的图象记为G.(1)、当点O在图象G上时,求a的值.(2)、当图象G的对称轴与直线x=2之间的部分的函数值y随x增大而减小时(直线x=2与对称轴不重合),求a的取值范围;(3)、以点A(0,﹣1)为对称中心,以|4a|为边长作正方形,使该正方形的边与坐标轴平行或垂直.若图象G与该正方形的某条边只有两个交点,且两个交点之间的距离为|a|,直接写出a的值.25. 已知,AB是⊙O的直径,AB= ,AC=BC. (1)、求弦BC的长;(2)、若点D是AB下方⊙O上的动点(不与点A,B重合),以CD为边,作正方形CDEF,如图1所示,若M是DF的中点,N是BC的中点,求证:线段MN的长为定值;(3)、如图2,点P是动点,且AP=2,连接CP,PB,一动点Q从点C出发,以每秒2个单位的速度沿线段CP匀速运动到点P,再以每秒1个单位的速度沿线段PB匀速运动到点B,到达点B后停止运动,求点Q的运动时间t的最小值.
(1)、求弦BC的长;(2)、若点D是AB下方⊙O上的动点(不与点A,B重合),以CD为边,作正方形CDEF,如图1所示,若M是DF的中点,N是BC的中点,求证:线段MN的长为定值;(3)、如图2,点P是动点,且AP=2,连接CP,PB,一动点Q从点C出发,以每秒2个单位的速度沿线段CP匀速运动到点P,再以每秒1个单位的速度沿线段PB匀速运动到点B,到达点B后停止运动,求点Q的运动时间t的最小值.