广东省深圳市坪山区2022年九年级4月模拟(二模)数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. -2022的绝对值是( )A、 B、 C、2022 D、-20222. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )A、 B、 C、 D、3.
如图所示的几何体的主视图为( )
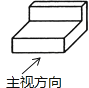 A、
A、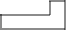 B、
B、 C、
C、 D、
D、 4. “科学用眼,保护视力”是青少年珍爱生命的具体表现,某班48名同学的视力检查数据如下表:
4. “科学用眼,保护视力”是青少年珍爱生命的具体表现,某班48名同学的视力检查数据如下表:视力
4.3
4.4
4.5
4.6
4.7
4.8
4.9
5.0
人数
2
3
6
9
12
8
5
3
则视力的众数和中位数分别是( )
A、4.5,4.6 B、4.6,4.6 C、4.7,4.7 D、4.8,4.75. 不等式组 的解集是( )A、x> B、﹣1≤x< C、x< D、x≥﹣16. 下列计算正确的是( )A、 B、 C、 D、7. 如图,点A的坐标为(1,3),点B在x轴上,把 沿x轴向右平移到 ,若四边形ABDC的面积为9,则点C的坐标为( )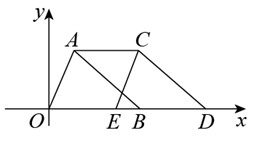 A、(1,4) B、(3,4) C、(3,3) D、(4,3)8. 如图是某地滑雪运动场大跳台简化成的示意图.其中AB段是助滑坡,倾斜角 ,BC段是水平起跳台,CD段是着陆坡,倾斜角 , , .若整个赛道长度(包括AB、BC、CD段)为270m,平台BC的长度是60m,整个赛道的垂直落差AN是114m.则AB段的长度大约是( ).
A、(1,4) B、(3,4) C、(3,3) D、(4,3)8. 如图是某地滑雪运动场大跳台简化成的示意图.其中AB段是助滑坡,倾斜角 ,BC段是水平起跳台,CD段是着陆坡,倾斜角 , , .若整个赛道长度(包括AB、BC、CD段)为270m,平台BC的长度是60m,整个赛道的垂直落差AN是114m.则AB段的长度大约是( ).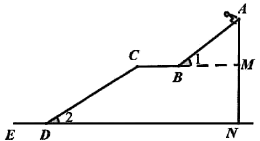 A、80m B、85m C、90m D、95m9. 二次函数 的图象如图所示,其与x轴交于点A(m,0),点B,下列4个结论:① ;② ;③ 有两个不相等的实数根;④ .其中正确的是( )
A、80m B、85m C、90m D、95m9. 二次函数 的图象如图所示,其与x轴交于点A(m,0),点B,下列4个结论:① ;② ;③ 有两个不相等的实数根;④ .其中正确的是( )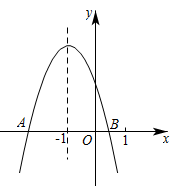 A、①② B、①③ C、①③④ D、①②③④10. 如图,在 中,D是BC边上的中点,连接AD,把 沿AD翻折,得到 , 与AC交于点E,若 , , ,则 的面积是( )
A、①② B、①③ C、①③④ D、①②③④10. 如图,在 中,D是BC边上的中点,连接AD,把 沿AD翻折,得到 , 与AC交于点E,若 , , ,则 的面积是( )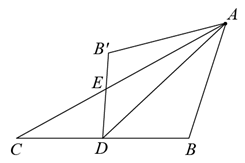 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 2022年冬奥会的主题口号是“一起向未来”,从5张上面分别写着“一”“起”“向”“未”“来”这5个字的卡片(大小,形状完全相同)中随机抽取一张,则这张卡片上面恰好写着“来”字的概率是 .13. 如图,直角 中, ,根据作图痕迹,若 , ,则 cm.
 14. 如图,点A是函数 ( )的图象上任意一点, 轴交函数 ( )的图象于点B,以AB为边作平行四边形ABCD,且 ,C、D在x轴上,则 .
14. 如图,点A是函数 ( )的图象上任意一点, 轴交函数 ( )的图象于点B,以AB为边作平行四边形ABCD,且 ,C、D在x轴上,则 . 15. 如图,在平行四边形ABCD中,E为CD中点,连接BE,F为BE中点,连接AF,若 , , .则AF长为 .
15. 如图,在平行四边形ABCD中,E为CD中点,连接BE,F为BE中点,连接AF,若 , , .则AF长为 .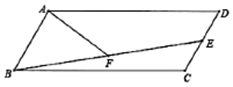
三、解答题
-
16. 计算: .17. 如图,在平面直角坐标系内, 三个顶点的坐标分别为A(-2,3),B(-5,2),C(-1,0).(正方形网格中,每个小正方形的边长是1个单位长度)
 (1)、将 沿y轴负方向平移3个单位得到 ,请画出 .(2)、求出 的面积.18. 6月14日是“世界献血日”,某市组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
(1)、将 沿y轴负方向平移3个单位得到 ,请画出 .(2)、求出 的面积.18. 6月14日是“世界献血日”,某市组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型
A
B
AB
O
人数
*
10
5
*
(1)、这次随机抽取的献血者人数为人,m= ;(2)、本次抽取的样本中,A型部分所占的圆心角的度数是°;(3)、若这次活动中该市有3000人义务献血,请你根据抽样结果估计这3000人中大约有多少人是A型血?19. 如图,AB是 的直径,弦 ,E是OB的中点,连接CE并延长到点F,使 ,连接AF交 于点D,连接BD,BF. (1)、求证:直线BF是 的切线;(2)、若AF长为 ,求BD的长.20. 某超市计划购进甲、乙两种水果进行销售.经了解,甲种水果和乙种水果的进价与售价如下表所示:
(1)、求证:直线BF是 的切线;(2)、若AF长为 ,求BD的长.20. 某超市计划购进甲、乙两种水果进行销售.经了解,甲种水果和乙种水果的进价与售价如下表所示:水果单价
甲
乙
进价(元/千克)
售价(元/千克)
20
25
已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.
(1)、求甲、乙两种水果的进价;(2)、若该超市购进这两种水果共100千克,其中甲种水果的重量不低于乙种水果重量的3倍,若全部卖完所购进的这两种水果,则超市应如何进货才能获得最大利润,最大利润是多少?21. 如图,直线 与x轴交于点A,与抛物线 交于抛物线的顶点C(1,4),抛物线 与x轴的一个交点是点B(3,0),点P是抛物线 上的一个动点. (1)、m=;点A的坐标是;抛物线的解析式是;(2)、如图2,若点P在第一象限,当 时,求出点P的坐标;(3)、如图3,CP所在直线交x轴于点D,当 是等腰三角形时,直接写出点P的坐标.22.(1)、【探究发现】
(1)、m=;点A的坐标是;抛物线的解析式是;(2)、如图2,若点P在第一象限,当 时,求出点P的坐标;(3)、如图3,CP所在直线交x轴于点D,当 是等腰三角形时,直接写出点P的坐标.22.(1)、【探究发现】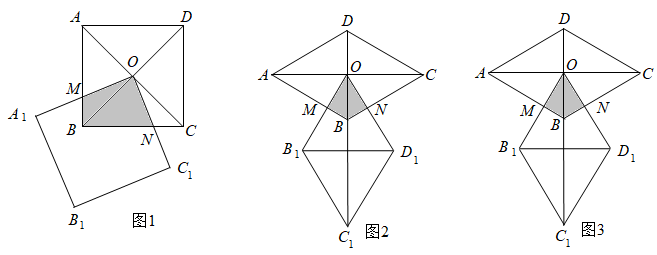
如图1,正方形ABCD两条对角线相交于点O,正方形 与正方形ABCD的边长相等,在正方形 绕点O旋转过程中,边 交边AB于点M,边 交边BC于点N.
①线段BM、BN、AB之间满足的数量关系是;
②四边形OMBN与正方形ABCD的面积关系是 ;
(2)、【类比探究】如图2,若将(1)中的“正方形ABCD”改为“含60°的菱形ABCD”,即 ,且菱形 与菱形ABCD的边长相等.当菱形 绕点O旋转时,保持边 交边AB于点M,边 交边BC于点N.
请猜想:
①线段BM、BN与AB之间的数量关系是 ▲ ;
②菱形OMBN与菱形ABCD的面积关系是 ▲ ;
请你证明其中的一个猜想.
(3)、【拓展延伸】如图3,把(2)中的条件“ ”改为“ ”,其他条件不变,则
① ;(用含α的式子表示)
② . (用含α的式子表示)