广东省深圳市南山区十校2022年九年级4月模拟（二模）数学试题

试卷更新日期：2022-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 2022的倒数是（）

A、﹣2022 B、2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 小明家购买了一款新型吹风机.如图所示，吹风机的主体是由一个空心圆柱体构成，手柄可近似看作一个圆柱体，这个几何体的主视图为（）

A、 B、 C、 D、

查看试题解析
3. 2022年2月8日，在北京冬奥会自由式女子大跳台金牌决赛中，中国选手谷爱凌以188.25分夺得金牌.北京冬奥会大数据报告显示，这场比赛受到我国超过5650万人的关注，5650万这个数字用科学记数法表示为（）

A、 $5.6 \times 1 0^{7}$ B、 $5.65 \times 1 0^{7}$ C、 $5.65 \times 1 0^{8}$ D、 $56.5 \times 1 0^{6}$

查看试题解析
4. 下列运算正确的是（）

A、 $2 + \sqrt{2} = 2 \sqrt{2}$ B、 $4 x^{2} y - x^{2} y = 3$ C、 $(a + b)^{2} = a^{2} + b^{2}$ D、 $(a b)^{3} = a^{3} b^{3}$

查看试题解析
5. 不等式 $- 2 x \leq - x + 2$ 的解在数轴上的表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 甲、乙、丙、丁四名射击运动员参加射击预选赛，他们射击成绩的平均数及方差如表所示，要选一个成绩较好且稳定的运动员去参赛，应选运动员（）
统计量
甲
乙
丙
丁
x（环）
7
8
8
7
S²（环²）
0.9
1.1
0.9
1

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 某书店分别用500元和700元两次购进一本小说，第二次数量比第一次多4套，且两次进价相同.若设该书店第一次购进x套，根据题意，列方程正确的是（）

A、 $\frac{500}{x} = \frac{700}{x - 4}$ B、 $\frac{500}{x - 4} = \frac{700}{x}$ C、 $\frac{500}{x} = \frac{700}{x + 4}$ D、 $\frac{500}{x + 4} = \frac{700}{x}$

查看试题解析
8. 已知现有的12瓶饮料中有2瓶已过了保质期，从这12瓶饮料中任取1瓶，恰好取到已过了保质期的饮料的概率是（）

A、 $\frac{1}{12}$ B、 $\frac{5}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
9. 数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是（）

A、射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”； B、车轮做成圆形，应用了“圆是中心对称图形”； C、学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”； D、地板砖可以做成矩形，应用了“矩形对边相等”．

查看试题解析
10. 现由边长为 $2 \sqrt{2}$ 的正方形ABCD制作的一副如图1所示的七巧板，将这副七巧板在矩形EFGH内拼成如图2所示的“老虎”造型，则矩形EFGH与“老虎”的面积之比为（）

A、2 B、 $\frac{6}{5}$ C、 $\frac{4}{3}$ D、 $\frac{15}{8}$

查看试题解析

二、填空题

11. $4 \sin 45 ° - \sqrt{8} + {(2 - \sqrt{3})}^{0}$ = ．

查看试题解析
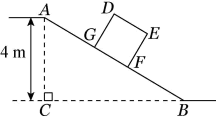
12. 某仓储中心有一斜坡AB，其坡比i＝1：2，顶部A处的高AC为4米，B、C在同一水平面上.则斜坡AB的水平宽度BC为米.

查看试题解析
13. 已知四边形ABCD内接于⊙O，∠ABC=70°，则∠ADC的度数是.

查看试题解析
14. 如图，点P在双曲线y= $\frac{k}{x}$ （x＞0）上，以P为圆心的⊙P与两坐标轴都相切，点E为y轴负半轴上的一点，过点P作PF⊥PE交x轴于点F，若OF﹣OE=8，则k的值是．

查看试题解析
15. 一副三角板按如图1放置，图2为简图，D为AB中点，E、F分别是一个三角板与另一个三角板直角边AC、BC的交点，已知AE=2，CE=5，连接DE，M为BC上一点，且满足∠CME=2∠ADE，EM= ．

查看试题解析

三、解答题

16. 化简 $\frac{x^{2} - 4 x + 4}{x - 1} \div (x - 2) + \frac{1}{x - 1}$

查看试题解析

17. 为了解某学校疫情期间学生在家体育锻炼情况，从全体学生中随机抽取若干名学生进行调查．以下是根据调查数据绘制的统计图表的一部分，根据信息回答下列问题．

组别	平均每日体育锻炼时间（分）	人数
A	0≤x≤15	9
B	15＜x≤25
C	25＜x≤35	21
D	x＞35	12

(1)、本次调查共抽取名学生．

(2)、抽查结果中，B组有人．

(3)、在抽查得到的数据中，中位数位于组（填组别）．

(4)、若这所学校共有学生2400人，则估计平均每日锻炼超过25分钟有多少人？

查看试题解析

18. 已知，如图，矩形ABCD，延长AB至点E，使得BE=AB，连接BD、CE.

(1)、求证：∠ABD=∠BEC.

(2)、AD=2，AB=3，连接DE，求sin∠AED的值.

查看试题解析
19. 图1是新冠疫情期间测温员用“额温枪”对居民张阿姨测温时的实景图，图2是其侧面示意图，其中枪柄CD和手臂BC始终在同一条直线上，枪身DE与额头F保持垂直.胳膊 $A B = 24 c m$ ， $B D = 40 c m$ ，肘关节B与枪身端点E之间的水平宽度为28cm（即BH的长度），枪身 $D E = 8 c m$ .

(1)、求 $∠ E D C$ 的度数；

(2)、测温时规定枪身端点E与额头规定范围为 $3 c m ∼ 5 c m$ .在图2中若 $∠ A B C = 75 °$ ，张阿姨与测温员之间的距离为48cm.问此时枪身端点E与张阿姨额头F的距离是否在规定范围内，并说明理由.（结果保留小数点后两位.参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
20. 某学校STEAM社团在进行项目化学习时，根据古代的沙漏模型（图1）制作了一套“沙漏计时装置”，该装置由沙漏和精密电子秤组成，电子秤上放置盛沙容器．沙子缓慢匀速地从沙漏孔漏到精密电子称上的容器内，可以通过读取电子秤的读数计算时间（假设沙子足够）．该实验小组从函数角度进行了如下实验探究：
实验观察：实验小组通过观察，每两小时记录一次电子秤读数，得到下表．

漏沙时间x（h）

0

2

4

6

8

电子秤读数y（克）

6

18

30

42

54

(1)、探索发现：建立平面直角坐标系，如图2，横轴表示漏沙时间x，纵坐标表示精密电子称的读数y，描出以表中的数据为坐标的各点．

(2)、观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，请你建立适当的函数模型，并求出函数表达式，如果不在同一条直线上，请说明理由．

(3)、结论应用：应用上述发现的规律估算：若漏沙时间为9小时，精密电子称的读数为多少？

(4)、若本次实验开始记录的时间是上午7：30，当精密电子秤的读数为72克时是几点钟？

查看试题解析
21. 如图已知二次函数 $y = x^{2} + b x + c$ （b，c为常数）的图像经过点A（3，-1），点C（0，-4）顶点为点M，过点A作AB $∥$ x轴，交y轴于点D，交二次函数 $y = x^{2} + b x + c$ 的图象于点B，连接BC．

(1)、求该二次函数的表达式及点M的坐标；

(2)、若将该二次函数图象向上平移m（m>0）个单位，使平移后得到的二次函数图象的顶点落在△ABC的内部（不包括△ABC的边界），求m的取值范围；

(3)、点P是直线AC上的动点，若点P，点C，点M所构成的三角形与△BCD相似，请直接写出所有点P的坐标（直接写出结果，不必写解答过程）．

查看试题解析
22. 如图1，正方形ABCD中，AC为对角线，点P在线段AC上运动，以DP为边向右作正方形DPFE，连接CE；

(1)、【初步探究】
则AP与CE的数量关系是， AP与CE的夹角度数为；

(2)、【探索发现】
点P在线段AC及其延长线上运动时，如图1，图2，探究线段DC，PC和CE三者之间的数量关系，并说明理由；

(3)、【拓展延伸】
点P在对角线AC的延长线上时，如图3，连接AE，若AB= $2 \sqrt{2}$ ，AE= $2 \sqrt{13}$ ，求四边形DCPE的面积．

查看试题解析

统计量	甲	乙	丙	丁
x（环）	7	8	8	7
S²（环²）	0.9	1.1	0.9	1

漏沙时间x（h）	0	2	4	6	8
电子秤读数y（克）	6	18	30	42	54