广东省深圳市龙华区2022年九年级4月调研测试（二模）数学试题

试卷更新日期：2022-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 现实生活中经常用正数和负数来表示具有相反意义的量．如果收入80元记作+80元，那么-20元表示（）

A、支出80元 B、收入80元 C、支出20元 D、收入20元

查看试题解析
2. 在厦门举办的金砖国家领导人第九次会晤和新兴市场国家与发展中国家对话会上，有一套瓷器餐具“先生瓷·海上明珠”令人瞩目．如图是餐具“先生瓷·海上明珠”中的一个瓷碗．关于这个瓷碗的三视图，下列说法正确的是（）

A、主视图与俯视图相同 B、主视图与左视图相同 C、左视图与俯视图相同 D、三种视图都相同

查看试题解析
3. 根据统计，某奥林匹克旗舰店销售额从 2 月初开始猛增，在开幕式 2 月 4 日当天达到最高值，达到 1160万元．其中数据 1160 万用科学记数法表示为（）

A、0.116×10⁴万 B、1.16×10³万 C、11.6×10²万 D、116×10 万

查看试题解析
4. 下列计算错误的是（）

A、 $a^{3} + a^{3} = 2 a^{3}$ B、 $a^{6} \div a^{2} = a^{4}$ C、 ${(a^{3})}^{2} = a^{6}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
5. 如图，∠1＝∠2＝58°，根据尺规作图痕迹，可得∠ADB 的度数是（）

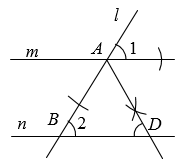A、58° B、60° C、61° D、122°

查看试题解析
6. 4月8日起，深圳“分级、分区、分批”有序推进各级各类学校（园）返校复课．学校要求学生每日测量体温．某同学连续 14 天的体温情况如下表所示，则该同学这 14 天的体温数据的众数和中位数分别是（）

体温（℃）

36.2

36.3

36.4

36.5

36.6

36.7

天数

1

4

3

3

2

1

A、36.3 和 36.4 B、36.3 和 36.45 C、36.3 和 36.5 D、36.7 和 36.3

查看试题解析
7. 某城市在旧城改造过程中，需要整修一段全长3000m的道路．为了尽量减少施工对城市交通造成的影响，实际工作效率比原计划提高了20%，结果提前10天完成任务．若设原计划每天整修道路x米，根据题意可得方程（）

A、 $\frac{3000}{x} - \frac{3000}{x (1 - 20 %)} = 10$ B、 $\frac{3000}{x (1 - 20 %)} - \frac{3000}{x} = 10$ C、 $\frac{3000}{x (1 + 20 %)} - \frac{3000}{x} = 10$ D、 $\frac{3000}{x} - \frac{3000}{x (1 + 20 %)} = 10$

查看试题解析
8. 下列说法正确的是（）

A、相等的角是对顶角 B、平行四边形是中心对称图形 C、绝对值相等的两个数相等 D、抛物线y＝x²-2x与坐标轴有3个不同的交点

查看试题解析
9. 如图，一次函数y＝2x+3的图像交y轴于点A，交x轴于点B，点P在线段AB上（不与A，B重合），过点P分别作OB和OA的垂线，垂足分别为C，D．当矩形OCPD的面积为1时，点P的坐标为（）

A、 $(- \frac{1}{2} ， 2)$ B、（-1，1） C、 $(- \frac{1}{2} ， 2)$ 或（-1，1） D、不存在

查看试题解析
10. 如图，在平行四边形ABCD中，AB=2AD，M为AB的中点，连接DM，MC，BD．下列结论中：①DM⊥MC；② $\frac{S_{Δ A D M}}{S_{Δ C D N}} = \frac{3}{4}$ ；③当DM＝DA时，△DMN≌△CBN；④当∠DNM＝45°时， $\tan ∠ A = \frac{\sqrt{2}}{2}$ 其中正确的结论是（）

A、①②③ B、①③④ C、①②④ D、①②③④

查看试题解析

二、填空题

11. 分解因式：3-3x²＝．

查看试题解析
12. 一道单项选择题有 A、B、C、D 四个备选答案，当你不会做的时候，从中随机地选一个答案，你答对的概率为．

查看试题解析
13. 如图，一名患者体内某重要器官后面有一肿瘤在 A 处．在接受放射性治疗时，为了最大限度地保证疗效，并且防止伤害器官，射线必须从侧面照射肿瘤．已知射线从肿瘤右侧 10cm 的 B 处进入身体，且射线与皮肤所成的夹角为∠CBA＝32.7°，则肿瘤在皮下的深度 AC 约为cm．
【参考数据：sin32.7°≈0.54，cos32.7°≈0.84，tan32.7°≈0.64】．

查看试题解析
14. 如图，点 A 是反比例函数 $y = \frac{k}{x}$ （k≠0，x<0）图象上的一点，经过点 A 的直线与坐标轴分别交于点C和点D，过点A作AB⊥y轴于点B， $\frac{B D}{O D} = \frac{1}{2}$ ，连接BC，若△BCD的面积为2，则k的值为．

查看试题解析
15. 如图，在△ABC 中，AB＝AC＝10，BC＝16，点 O 是△ABC 的重心，将线段 AO 绕点 A 逆时针旋转至 O′，点 D 为线段 CO′的中点，连接 BD，则 BD 的最大值为．

查看试题解析

三、解答题

16. 计算： ${(2022 - π)}^{0} - {(\frac{1}{2})}^{- 2} + \sqrt{27} - 3 \tan 60 °$ ．

查看试题解析
17. 先化简，再求值： $\frac{2 x}{x + 2} - \frac{x^{2} - 4}{x^{2} + 4 x + 4} \div \frac{x - 2}{x}$ ，其中x=1．

查看试题解析
18. 第24届冬季奥林匹克运动会，又称2022年北京冬奥会，于2022年2月4日至2月20日在北京市和张家口市同时举行，为了调查同学们对冬奥知识的了解情况，某学校组织了“冬奥知识知多少”竞赛活动，并随机抽取了部分学生的竞赛成绩进行分析，共分为六个等级：A+，A，B+，B，C+，C，并绘制了如下不完整的统计图．

请结合统计图表，回答下列问题：

(1)、本次抽样的学生人数为人；

(2)、请补全条形统计图；

(3)、扇形统计图中“A等级”所在扇形的圆心角是°；

(4)、若该校共有学生3000人，请估计该校学生对冬奥知识的了解程度为“A+和A等级”的学生约有人．

查看试题解析
19. 如图，在△ACD中，点B为AC边上的点，以AB为直径的⊙O与CD相切于点E，连接AE，∠D＝2∠EAC．

(1)、求证：AD是⊙O的切线；

(2)、若∠D＝60°，⊙O的半径为4，求阴影部分的面积．（结果保留根号和π）

查看试题解析
20. 开学前夕，某书店计划购进 A、B 两种笔记本共 350 本．已知 A 种笔记本的进价为 12 元/本，B 种笔记本的进价为 15 元/本，共计 4800 元．

(1)、请问购进了A种笔记本多少本？

(2)、在销售过程中，A、B两种笔记本的标价分别为20元/本、25元/本．受疫情影响，两种笔记本按标价各卖出m本以后，该店进行促销活动，剩余的A种笔记本按标价的七折全部售出，剩余的B种笔记本按成本价清货，若两种笔记本的总利润不少于2348元，请求出m的最小值．

查看试题解析
21. 已知抛物线 y = ax²+ bx+2 经过点 A （-2，0）．

(1)、b＝（用含 a 的代数式表示）；

(2)、若抛物线 y = ax²+ bx+2 与 x 轴的另一交点为 B，且 AB＝3．求 a 的值；

(3)、在（2）的条件下，当 a 为整数时，记抛物线的顶点为 M．现将该抛物线进行平移，使平移后的抛物线的顶点在直线 OM 上运动．当平移后的抛物线恰好经过原点时，求平移后的抛物线的解析式．

查看试题解析
22. 某“数学学习兴趣小组”成员在复习《图形的变化》时，对下面的图形背景产生了浓厚的兴趣，并尝试运用由“特殊到一般”的思想进行了探究：

(1)、【问题背景】如图1，正方形ABCD中，点E为AB边上一点，连接DE，过点E作EF⊥DE交BC边于点F，将△ADE沿直线DE折叠后，点A落在点 $A^{'}$ 处，当∠BEF＝25°，则∠FE $A^{'}$ ＝°．

(2)、【特例探究】如图2，连接DF，当点 $A^{'}$ 恰好落在DF上时，求证：AE＝2 $A^{'}$ F．

(3)、【深入探究】若把正方形ABCD改成矩形ABCD，且AD＝mAB，其他条件不变，他们发现AE与 $A^{'}$ F之间也存在着一定的数量关系，请直接写出AE与 $A^{'}$ F之间的数量关系式．

(4)、【拓展探究】若把正方形ABCD改成菱形ABCD，且∠B＝60°，∠DEF＝120°，其他条件不变，他们发现AE与 $A^{'}$ F之间也存在着一定的数量关系，请直接写出AE与A′F之间的数量关系式．

查看试题解析

体温（℃）	36.2	36.3	36.4	36.5	36.6	36.7
天数	1	4	3	3	2	1