广东省深圳市福田区2022年九年级4月质量检测数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
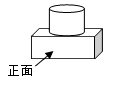
1. 2022的倒数是( )A、﹣2022 B、2022 C、 D、2. 如图是由一个圆柱和一个长方体组成的几何体,则该几何体的俯视图是( )
 A、
A、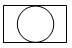 B、
B、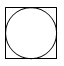 C、
C、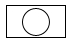 D、
D、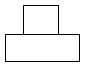 3. 2022年北京冬奥,越来越多的北京市民加入到了志愿者队伍里去.据北京市冬奥会城市志愿者指挥部宣传教育组副组长王欣透露,全市实名注册志愿者人数突破449.3万人.其中449.3万用科学记数法表示为( )A、 B、 C、 D、4. 用不等式表示图中的解集,以下选项正确的是( )
3. 2022年北京冬奥,越来越多的北京市民加入到了志愿者队伍里去.据北京市冬奥会城市志愿者指挥部宣传教育组副组长王欣透露,全市实名注册志愿者人数突破449.3万人.其中449.3万用科学记数法表示为( )A、 B、 C、 D、4. 用不等式表示图中的解集,以下选项正确的是( ) A、 B、 C、 D、5. 在学校举行“阳光少年,励志青春”的演讲比赛中,五位评委给选手小明的评分分别为:90,85,90,80,95,则这组数据的众数是( )A、95 B、90 C、85 D、806. 下列计算结果正确的是( )A、 B、 C、 D、7. 下列说法正确的是 ( )A、线段的垂直平分线上的点到这条线段两个端点的距离相等 B、已知反比例函数 , 随 的增大而减小 C、平分弦的直径垂直于弦 D、对角线互相垂直的四边形是菱形8. 如图, ABC与 DEF位似,点O是位似中心,若OE=3OB, =4,则 =( )
A、 B、 C、 D、5. 在学校举行“阳光少年,励志青春”的演讲比赛中,五位评委给选手小明的评分分别为:90,85,90,80,95,则这组数据的众数是( )A、95 B、90 C、85 D、806. 下列计算结果正确的是( )A、 B、 C、 D、7. 下列说法正确的是 ( )A、线段的垂直平分线上的点到这条线段两个端点的距离相等 B、已知反比例函数 , 随 的增大而减小 C、平分弦的直径垂直于弦 D、对角线互相垂直的四边形是菱形8. 如图, ABC与 DEF位似,点O是位似中心,若OE=3OB, =4,则 =( ) A、9 B、12 C、16 D、369. 已知抛物线 与 轴交于 , 两点,将这条抛物线的顶点记为 ,连结 , ,则 的值为( )A、 B、 C、 D、10. 如图,矩形 中, , , , 分别是 , 上的两个动点, , 沿 翻折形成 ,连接 , ,则 的最小值是( )
A、9 B、12 C、16 D、369. 已知抛物线 与 轴交于 , 两点,将这条抛物线的顶点记为 ,连结 , ,则 的值为( )A、 B、 C、 D、10. 如图,矩形 中, , , , 分别是 , 上的两个动点, , 沿 翻折形成 ,连接 , ,则 的最小值是( ) A、5 B、4 C、 D、
A、5 B、4 C、 D、二、填空题
-
11. 分解因式:2a2+4a+2= .12. 已知关于 的方程 有两个相等的实数根,则 的值是..13.
如图,在△ABC中,按以下步骤作图:
①分别以点A、C为圆心,以大于AC的长为半径画弧,两弧相交于M、N两点;
②作直线MN交BC于点D,连接AD,
若∠C=28°,AB=BD,则∠B的度数为 .
 14. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,点 在第一象限内,连接 、 .已知 ,则 .
14. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,点 在第一象限内,连接 、 .已知 ,则 . 15. 如图,四边形OABC是平行四边形,点C在x轴上,反比例函数 的图象经过点 ,且与边BC交于点 若 ,则点D的坐标为 .
15. 如图,四边形OABC是平行四边形,点C在x轴上,反比例函数 的图象经过点 ,且与边BC交于点 若 ,则点D的坐标为 .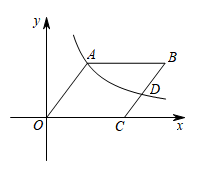
三、解答题
-
16. 计算:17. 化简求值: ,其中 ;18. 某中学数学兴趣小组为了解本校学生对春节联欢晚会中五类节目的喜欢情况,其中 :歌曲、 :舞蹈、 :魔术、 :小品、 :相声,随机抽取了部分学生进行调查(被调查的学生只选一类并且没有不选的),并将调查结果绘制成如图所示的不完整的条形图和扇形图.请根据图中所给出的信息解答下列问题:
 (1)、本次抽样调查的样本容量是;(2)、请补全条形图;(3)、扇形图中, , 节目类型 对应的扇形圆心角的度数是°;(4)、若该中学有1800名学生,那么该校喜欢歌曲节目的学生大约有多少人?19. 如图,已知在⊙O中, ,OC与AD相交于点E.求证:
(1)、本次抽样调查的样本容量是;(2)、请补全条形图;(3)、扇形图中, , 节目类型 对应的扇形圆心角的度数是°;(4)、若该中学有1800名学生,那么该校喜欢歌曲节目的学生大约有多少人?19. 如图,已知在⊙O中, ,OC与AD相交于点E.求证: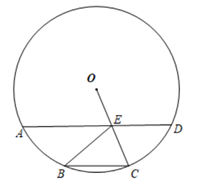 (1)、AD∥BC(2)、四边形BCDE为菱形.20. 2022北京冬奥会吉祥物“冰墩墩”成为了热销品,某合作商家准备推出钥匙扣和毛绒玩具两种“冰墩墩”商品.已知每个钥匙扣的单价比毛绒玩具低40元,销售50个钥匙扣与销售10个毛绒玩具的总价相同.(1)、求钥匙扣、毛绒玩具的单价.(2)、已知单个钥匙扣的成本为6元,单个毛绒玩具的成本是36元.第一阶段商家计划用不超过1260元的成本制作钥匙扣和毛绒玩具共60个进行销售,且钥匙扣的数量不高于毛绒玩具的2倍.则钥匙扣、毛绒玩具各销售多少个可获得最大利润?最大利润是多少?21. 定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)、AD∥BC(2)、四边形BCDE为菱形.20. 2022北京冬奥会吉祥物“冰墩墩”成为了热销品,某合作商家准备推出钥匙扣和毛绒玩具两种“冰墩墩”商品.已知每个钥匙扣的单价比毛绒玩具低40元,销售50个钥匙扣与销售10个毛绒玩具的总价相同.(1)、求钥匙扣、毛绒玩具的单价.(2)、已知单个钥匙扣的成本为6元,单个毛绒玩具的成本是36元.第一阶段商家计划用不超过1260元的成本制作钥匙扣和毛绒玩具共60个进行销售,且钥匙扣的数量不高于毛绒玩具的2倍.则钥匙扣、毛绒玩具各销售多少个可获得最大利润?最大利润是多少?21. 定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线. (1)、如图1,在 中, , 是 的角平分线, , 分别是 , 上的点。求证:四边形 是邻余四边形.(2)、如图2,在 的方格纸中,A, 在格点上,请画出一个符合条件的邻余四边形 ,使AB是邻余线, , 在格点上.(3)、如图3,在(1)的条件下,取 中点 ,连结 并延长交 于点 ,延长 交 于点 .若 为 的中点, , ,求邻余线 的长.22. 如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,抛物线经过点 和点 ,点 是第一象限抛物线上的一个动点.
(1)、如图1,在 中, , 是 的角平分线, , 分别是 , 上的点。求证:四边形 是邻余四边形.(2)、如图2,在 的方格纸中,A, 在格点上,请画出一个符合条件的邻余四边形 ,使AB是邻余线, , 在格点上.(3)、如图3,在(1)的条件下,取 中点 ,连结 并延长交 于点 ,延长 交 于点 .若 为 的中点, , ,求邻余线 的长.22. 如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,抛物线经过点 和点 ,点 是第一象限抛物线上的一个动点. (1)、求直线 和抛物线的表达式;(2)、在 轴上取点 ,连接 , ,当四边形 的面积是 时,求点 的坐标;(3)、在(2)的条件下,当点 在抛物线对称轴的左侧时,直线 上存在两点 , (点 在点 的上方),且 ,动点 从点 出发,沿 的路线运动到终点 ,当点 的运动路程最短时,请直接写出点 的坐标.
(1)、求直线 和抛物线的表达式;(2)、在 轴上取点 ,连接 , ,当四边形 的面积是 时,求点 的坐标;(3)、在(2)的条件下,当点 在抛物线对称轴的左侧时,直线 上存在两点 , (点 在点 的上方),且 ,动点 从点 出发,沿 的路线运动到终点 ,当点 的运动路程最短时,请直接写出点 的坐标.