备考浙教版中考数学题型专项训练一次函数解答题专练-在线组卷题库

1. 如图1，直线y=

- \frac{3}{4}

x+6分别交x轴，y轴于点A，点B，点C、P分别是线段OB，AB的中点，动点D，E分别在直线CP和线段AB上，设点E的横坐标为m，线段CD的长为n（n>0），且m+n=6，以DO，DE为邻边作▱ ODEF．

(1)、求点A和点P的坐标．

(2)、如图2所示，当点D在点C左侧，且n=2时，求点F的坐标．

(3)、当点F落在△AOB的边OB或AB上时，求点F的坐标．

查看试题解析

2. 如图，在平面直角坐标系中，点A，B的坐标分别是（﹣4，0），（0，8），动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP，CO为邻边构造▱PCOD，在线段OP延长线上取点E，使PE＝AO，设点P运动的时间为t秒．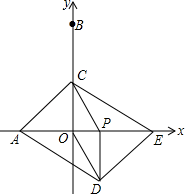

(1)、当点C运动到线段OB的中点时，求t的值及点E的坐标；

(2)、当点C在线段OB上时，求证：四边形ADEC为平行四边形；

(3)、在线段PE上取点F，使PF＝3，过点F作MN⊥PE，截取FM＝

\sqrt{3}

，FN＝1，且点M，N分别在第一、四象限，在运动过程中，当点M，N中，有一点落在四边形ADEC的边上时，直接写出所有满足条件的t的值．

查看试题解析

3. 在平面直角坐标系中，已知点A(a，0)，B（b，0），C（0，c），且

\sqrt{a + 1}

+3|b﹣3|＋2（c＋2）²=0．

(1)、直接写出S_△_ACB=；

(2)、如图1，线段CB沿y轴正方向以每秒0.5个单位的速度匀速移动至DE（点C的对应点为D，点B的对应点为E），连接AD、OE．设运动时间为t秒，问：是否存在这样的t值，使得3S_△_ACD＝2S_△_EOD？若存在，请求出t的值；若不存在，请说明理由．

(3)、如图2，将线段AC往右平移3个单位长度至FG（点A的对应点为点F），线段FG与BC相交于点H．若在x轴上存在点M使得S_△_MCH=2，试求出点M的坐标．

查看试题解析

4. 如图，在平面直角坐标系中，已知直线PA是一次函数y＝x+m（m＞0）的图象，直线PB是一次函数y＝﹣3x+n（n＞m）的图象，点P是两直线的交点，点A、B、C、Q分别是两条直线与坐标轴的交点.

(1)、用m、n分别表示点A、B、P的坐标及∠PAB的度数；

(2)、若四边形PQOB的面积是

\frac{11}{2}

，且

C Q = \frac{1}{2} A O

，试求点P的坐标，并求出直线PA与PB的函数表达式；

(3)、在（2）的条件下，是否存在一点D，使以A、B、P、D为顶点的四边形是平行四边形？若存在，求出点D的坐标；若不存在，请说明理由.

查看试题解析

5. 周末，小畅与妈妈沿相同的路线去爬山．因为乘坐交通工具不同，当小畅到达山脚下开始上山时，妈妈已经到达山顶并开始从山顶返回，在登山的过程中两人一直保持匀速运动，在山路中间有一个观光亭距离山顶30米．两人与观光亭的距离y（单位：m）与小畅登山时间x（单位：min）之间的函数图象如图所示．

(1)、求小畅的速度及b的值；

(2)、求妈妈在下山过程中y与x之间的函数解析式；

(3)、直接写出x为多少时，两人与观光亭的距离相等．

查看试题解析

6. 如图，在平面直角坐标系中，直线AB的解析式为

y = \frac{1}{2} x + 3

，它与x轴交于点B，与y轴交于点A，直线y=-x与直线AB交于点C．动点P从点C出发，以每秒1个单位长度的速度沿射线CO运动，运动时间为t秒．

(1)、求△AOC的面积；

(2)、设△PAO的面积为S，求S与t的函数关系式，并写出自变量的取值范围；

(3)、M是直线OC上一点，在平面内是否存在点N，使以A，O，M，N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析

7. 如图，lA、lB分别表示A步行与B骑车在同一公路上同时出发，距甲地的路程S（千米）与B出发的时间t（小时）的关系，已知B骑车一段路后，自行车发生故障，进行修理.

(1)、B出发时与A相距千米，B出发后小时与A相遇；

(2)、求出A距甲地的路程SA（千米）与时间t（小时）的关系式：

(3)、根据图中所给的信息：若B的自行车不发生故障，保持出发时的速度前进，在途中何时与A相距2km？

查看试题解析

8. “燃情冰雪，拼出未来”，北京冬奥会将于2022年2月4日如约而至．某商家已提前开始冬奥会吉祥物“冰墩墩”纪念品的销售．每个纪念品进价40元，规定销售单价不低于44元，且不高于52元．销售期间发现，当销售单价定为44元时，每天可售出300个，销售单价每上涨1元，每天销量减少10个．现商家决定提价销售，设每天销售量为

y

个，销售单价为

x

元．

(1)、直接写出

y

与

x

之间的函数关系式和自变量

x

的取值范围；

(2)、求当每个纪念品的销售单价是多少元时，商家每天获利2400元；

(3)、将纪念品的销售单价定为多少元时，商家每天销售纪念品获得的利润

w

元最大？最大利润是多少元？

查看试题解析

9. 如图1，在平而直角坐标系中，直线AB：y=

- \frac{4}{3}

x+4与坐标轴交于A，B两点，点C为AB的中点，动点P从点A出发，沿AO方向以每秒1个单位的速度向终点O运动，同时动点Q从点O出发，以每秒2个单位的速度沿射线OB方向运动，当点P到达点O时，点Q也停止运动．以CP，CQ为邻边构造

▱

CPDQ，设点P运动的时间为t秒．

(1)、直接写出点C的坐标为．

(2)、如图2，过点D作DG⊥y轴，过点C作CH⊥x轴．证明：△PDG≌△CQH．

(3)、如图3，连结OC，当点D恰好落在△OBC的边所在的直线上时，求所有满足要求的t的值．

查看试题解析

10. 在平面直角坐标系xOy中，A，B点的坐标分别为(0，4)，(-4，0)，P点坐标为(0，m)，点E是射线BO上的动点，满足BE=1.5OP，以PE，EO为邻边作 ▱ PEOQ．

(1)、当m=2时，求出PE的长度；

(2)、当m>0时，是否存在m的值，使得

▱

PEOQ的面积等于△ABO面积的

\frac{1}{4}

，若存在求出m的值，若不存在，请说明理由；

(3)、当点Q在第四象限时，点Q关于E点的对称点为Q'，点Q'刚好落在直线AB上时，求m的值(直接写出答案)．

查看试题解析

11. 已知抛物线y＝a（x﹣2）²（a≠0）交y轴于点B(0，2)，顶点为点A，且与直线l交于不同的两点M、N（M、N不与点A重合），点D(2，2)在直线l上．

(1)、求抛物线的解析式；

(2)、若点N的坐标为(6n，n)，且点N在抛物线对称轴的右侧，请证明∠MAN＝90°；

(3)、过点A作AE⊥l，垂足为点E，求点B到点E的最短距离．

查看试题解析

12. 在平面直角坐标系中，点A，B的坐标分别为

(2 \sqrt{2} ， 0)

、

(0 ， 1)

，点P的坐标为

(\frac{\sqrt{2}}{4} ， 0)

.点E是y轴上一动点，QP⊥EP交AB于点Q（保持点Q在x轴上方），EF⊥EQ交AB于点F.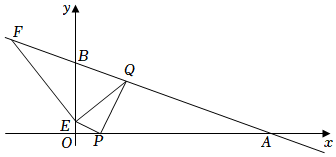

(1)、当PQ⊥AB时，求OE的长.

(2)、当点E在线段OB上移动时，设AQ＝n，OE＝m，求n关于m的函数表达式.

(3)、点E在射线OB上移动过程中，点Q、E、F构成的三角形与△OAB相似，求出点E的纵坐标.

查看试题解析

13. 【操作发现】

在计算器上输入一个正数，不断地按“”键求算术平方根，运算结果越来越接近1或都等于1.

【提出问题】

输入一个实数，不断地进行“乘以常数k，再加上常数b”的运算，有什么规律？

【分析问题】

我们可用框图表示这种运算过程（如图a）.

也可用图象描述：如图1，在x轴上表示出x₁ ，先在直线y=kx+b上确定点（x₁ ， y₁），再在直线y=x上确定纵坐标为y₁的点（x₂ ， y₁），然后再x轴上确定对应的数x₂ ， …，以此类推.

【解决问题】

研究输入实数x₁时，随着运算次数n的不断增加，运算结果x，怎样变化.

(1)、若k=2，b=﹣4，得到什么结论？可以输入特殊的数如3，4，5进行观察研究；

(2)、若k＞1，又得到什么结论？请说明理由；

(3)、①若

k = - \frac{2}{3}

， b=2，已在x轴上表示出x₁（如图2所示），请在x轴上表示x₂ ， x₃ ， x₄ ，并写出研究结论；

②若输入实数x₁时，运算结果xn互不相等，且越来越接近常数m，直接写出k的取值范围及m的值（用含k，b的代数式表示）

查看试题解析

14. 数学来源于生活，数学之美无处不在，在几何图形中，最美的角是45°，最美的直角三角形是等腰直角三角形，我们把45°的角称为一中美角，最美的等腰直角三角形称为一中美三角．根据该约定，完成下列问题：

(1)、如图1，已知正方形ABCD中O是对角线AC上一动点，过O作OP⊥OD，垂足为O，交BC边于P，△POD是否为一中美三角，并说明理由；

(2)、如图2，在平面直角坐标系中，点A（﹣2，0），点B（0，2），点P在第二象限内，且在直线y＝﹣2x﹣2上，若△ABP恰好构成一中美三角，求出此时P点的坐标；

(3)、如图3，若二次函数y＝﹣x²+2x+3的图象与x轴交于A、B两点，与y轴交于点C，P为第二象限上的点，在直线AC上，且∠OPB恰好构成一中美角；Q为x轴上方抛物线上的一动点，令Q点横坐标为m（0＜m＜3），当m为何值时，△PBQ的面积最大，求出此时Q点坐标和最大面积．

查看试题解析

15. 如图1，直线

y = - 2 x + 6

的图像与x轴、y轴分别交于A、B两点，点D是线段AB上一点，过D点分别作OA、OB的垂线，垂足分别是C、E，矩形OCDE的面积为4，且

C D > D E

．

(1)、求D点坐标；

(2)、将矩形OCDE以1个单位/秒的速度向右平移，平移后记为矩形MNPQ，记平移时间为t秒．

①如图2，当矩形MNPQ的面积被直线AB平分时，求t的值；

②如图3，当矩形MNPQ的边与反比例函数 $y = \frac{12}{x}$ 的图像有两个交点，记为T、K，若直线TK把矩形面积分成1：7两部分，请直接写出t的值．

查看试题解析

16. 如图，抛物线y＝﹣x²+bx+c与x轴交于A（﹣1，0），B两点（点A在点B的左侧），与y轴交于点C（0，3），作直线BC．动点P在x轴上运动，过点P作PM⊥x轴，交抛物线于点M，交直线BC于点N，设点P的横坐标为m．

(1)、求抛物线的解析式；

(2)、当点P在线段OB上运动时，求线段MN的最大值；

(3)、是否存在点P，使得以点C、O、M、N为顶点的四边形是平行四边形？若存在，请直接写出m的值；若不存在，请说明理由．

查看试题解析

17. 如图，在平面直角坐标系中，点A，B的坐标分别为

(3 ， 2)

，

(0 ， 8)

，以

A B

为直径的圆交y轴于点C，D为圆上一点，

\overset{⌢}{A C} = \overset{⌢}{C D}

，直线

A D

交x轴于点E，交y轴于点F，连结

O A

.

(1)、求

t a n ∠ A B C

的值和直线

A B

的函数表达式.

(2)、求点D，E的坐标.

(3)、动点P，Q分别在线段

O E

，

O A

上，连结

P Q

.若

P Q = 2

，当

P Q

与

△ A B D

的一边平行时，求所有满足条件的

O P

的长.

查看试题解析

18. 如图，直线

y = - 3 x + 3

分别交x轴、y轴于点A，B，以A为圆心，

A B

为半径作半圆，

A C ⊥ A B

交半圆弧于点C，弦

C D ∥ x

轴，交y轴正半轴于点E，连结

O D ， B D

.

(1)、求

⊙ A

的半径长及直线

B C

的函数表达式.

(2)、求

t a n ∠ A B D

的值.

(3)、P为x轴上一点.

①当 $P C$ 平行于四边形 $O A B D$ 的一边时，求出所有符合条件的 $A P$ 的长.

②若直线 $E P$ 恰好平分五边形 $O A C B D$ 的面积，求点P的横坐标.（直接写出答案即可）

查看试题解析

19. 已知直线l₁：y＝－2x＋10交y轴于点A，交x轴于点B，二次函数的图象过A，B两点，交x轴于另一点C，BC＝4，且对于该二次函数图象上的任意两点P₁（x₁ ， y₁），P₂（x₂ ， y₂），当x₁>x₂≥5时，总有y₁>y₂.

(1)、求二次函数的表达式；

(2)、若直线l₂：y＝mx＋n（n≠10），求证：当m＝－2时，l₂//l₁；

(3)、E为线段BC上不与端点重合的点，直线l₃：y＝－2x＋q过点C且交直线AE于点F，求

△ A B E

与

△ C E F

面积之和的最小值．

查看试题解析

20. 经研究表明，某市跨河大桥上的车流速度V（单位：千米/时）是车流密度x（单位：辆/千米）的函数，函数图象如图所示．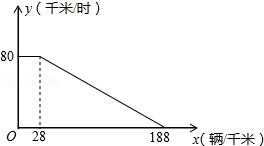

(1)、求当28≤x≤188时，关于x的函数表达式；

(2)、求车流量P（单位：辆/时）与车流密度x之间的函数关系式；（注：车流量是单位时间内通过观测点的车辆数，计算公式为：车流量=车流速度×车流密度）

(3)、若车流速度V不低于50千米时，求当车流密度x为多少时，车流量P达到最大，并求出这一最大值．

查看试题解析

21. 在平面直角坐标系中，直线y＝kx+4（k≠0）交x轴于点A（8，0），交y轴于点B，

(1)、k的值是；

(2)、点C是直线AB上的一个动点，点D和点E分别在x轴和y轴上．

①如图，点E为线段OB的中点，且四边形OCED是平行四边形时，求▱OCED的周长；

②当CE平行于x轴，CD平行于y轴时，连接DE，若△CDE的面积为 $\frac{33}{4}$ ，请直接写出点C的坐标．

查看试题解析

22. 在平面直角坐标系中，点O是坐标原点，A（0，4），点B在x轴负半轴上，且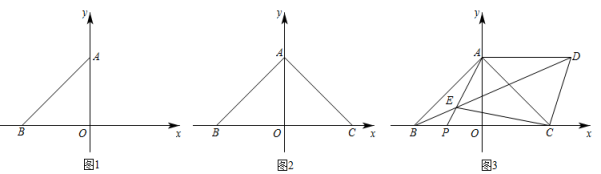

∠ A B O = 45 °

(1)、如图1，求B点坐标；

(2)、如图2，点C与点B关于y轴对称，点P从点B出发沿射线BC方向以每秒1个单位的速度运动，到点C停止运动，设动点P的运动时间为t（秒），连接AP，

△ A P O

的面积为S，求用含t的式子表示S（不必写出t的取值范围）；

(3)、如图3，在（2）的条件下，若点P在线段BO上，点D为第一象限一点，连接AD、BD、CD，BD与AP交于点E，连接EC，若

∠ D A C = 2 ∠ D B C

，

∠ P A O = ∠ A D B

，

B E = 2 \sqrt{2}

，求

△ B E C

的面积．

查看试题解析

23. 如图，点A、B分别在y轴正半轴，x轴负半轴上，OB=3，∠ABO=60°．

(1)、求直线AB解析式；

(2)、点C在x轴上点B的右侧，连接AC，将线段AC绕点A逆时针旋转60°得到AD，连接BD，求△ABD的面积；

(3)、在（2）的条件下，点E在x轴正半轴上，OE=AB，连接AE，点G为AE中点，射线DG交射线AB于点H，

\frac{G H}{D G} = \frac{O E}{O C}

，求点D的坐标

查看试题解析

24.

(1)、基本图形的认识：

如图1，在四边形ABCD中，∠B=∠C=90°，点E是边BC上一点，AB=EC，BE=CD，连结AE、DE，求证：△AED是等腰直角三角形．

(2)、基本图形的构造：

如图2，在平面直角坐标系中，A（2，0），B（0，3），连结AB，过点A在第一象限内作AB的垂线，并在垂线截取AC=AB，求点C的坐标；

(3)、基本图形的应用：

如图3，一次函数y=-2x+2的图象与y轴交于点A，与x轴交于点B，直线AC交x轴于点D，且∠CAB=45°，求点D的坐标．

查看试题解析

25. 问题探究

(1)、已知直线y＝kx+b经过点A（﹣3，0），B（0，﹣

\sqrt{3}

），当

- \sqrt{3} \leq x \leq 2 \sqrt{3}

时，求y的最小值．

(2)、如图1，等边△ABC中，AB=2，点D为边BC的中点，连接AD，求∠CAD及CD：AC：AD的值；

(3)、问题解决：如图2，在平面直角坐标系中，直线l与x轴、y轴分别交于点M、E，已知点M（-3，0），且∠EMO＝60°，点A（4，

\sqrt{3}

），B（2，﹣

\sqrt{3}

），C（﹣1，﹣2

\sqrt{3}

），连接AB，BC，得到折线段A﹣B﹣C，点P为折线段A﹣B﹣C上一动点，过点P向直线l作垂线，垂足为H，过点P作x轴的平行线交直线于点Q，则△PHQ的周长是否存在最大值或最小值？若存在，求出相应最值；若不存在，请说明理由.

查看试题解析

26. 如图，在平面直角坐标系中，

A (- 1 ， 0)

，

B (0 ， 3)

，直线

y = - \frac{1}{3} x + 1

与x轴相交于点C，与直线AB交于点D，交y轴于点E.

(1)、求直线AB的解析式及点D的坐标；

(2)、如图2，H是直线AB上位于第一象限内的一点，连接HC，当

S_{△ H C D} = \frac{72}{5}

时，点M、N为y轴上两动点，点M在点N的上方，且

M N = \frac{6}{5}

，连接HM、NC，求

H M + M N + N C

的最小值；

(3)、将△OEC 绕平面内某点转90°，旋转后的三角形记为

△ O^{'} E^{'} C^{'}

，若点

E^{'}

落在直线AB上，点

O^{'}

落在直线CD上，请直接写出满足条件的点

E^{'}

的坐标.

查看试题解析

27. 在平面直角坐标系中，点A的坐标为

(- 4 \sqrt{10} ， 0)

，点B在直线l：

y = \frac{1}{3} x

上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C.

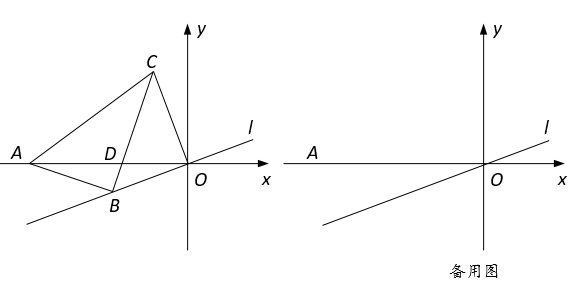(1)、如图，点B，C分别在第三、二象限内，BC与AO相交于点D，若BA=BO.

①求证：CD=CO.

②求四边形ABOC的面积.

(2)、是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB的长；若不存在，请说明理由.

查看试题解析

28. 如图，直线y＝kx+b与x轴、y轴分别交于点A（4，0）、B（0，4），点P在x轴上运动，连接PB，将△OBP沿直线BP折叠，点O的对应点记为O′．

(1)、求k、b的值；

(2)、若点O′恰好落在直线AB上，求△ABP的面积；

(3)、将线段PB绕点P顺时针旋转45°得到线段PC，直线PC与直线AB的交点为Q，在点P的运动过程中，是否存在某一位置，使得△PBQ为等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析

29. 如图所示，在平面直角坐标系xOy中，直线l₁：

y = \sqrt{3} x + \sqrt{3}

交x轴于点B，交y轴于点A，过点C（1，0）作x轴的垂线l₂ ，将直线l₂绕点C按逆时针方向旋转，旋转角为α（0°＜α＜180°）.

(1)、若直线l₂经过点A，①求线段AC的长；②直接写出旋转角α的度数；

(2)、若直线l₂在旋转过程中与y轴交于D点，当△ABD、△ACD、△BCD均为等腰三角形时，求出符合条件的旋转角α的度数.

(3)、若直线l₂在旋转过程中与直线l₁ 交于点E，连OE，以OE为边作等边△OEF（点O、E、F按逆时针方向排列），连BF.请你探究线段BE，OB与BF之间的数量关系？并说明理由。

查看试题解析

30. 如图，在直角坐标系中，一次函数y＝x+2的图象与x轴交于点A，与y轴交于点B，点C的坐标为（2，0），连接BC.

(1)、判断△ABC是不是等腰直角三角形，并说明理由：

(2)、若点P在线段BC的延长线上运动（P不与点C重合），连接AP，作AP的垂直平分线交y轴于点E，垂足为D，分别连接EA，EP；

①当点P在运动时，∠AEP的度数是否变化？若变化，请说明理由；若不变，求出∠AEP的度数；

②若点P从点C出发，运动速度为每秒1个单位长度，设△AOE的面积为S，点P的运动时间为t秒，求S关于t的函数关系式.

查看试题解析

31. 在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC，连接OB，点D为OB的中点，点E是线段AB上的动点，连接DE，作DF⊥DE，交OA于点F，连接EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．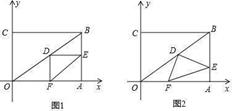

(1)、如图1，当t＝3时，求DF的长．

(2)、如图2，当点E在线段AB上移动的过程中，

\frac{D F}{D E}

的大小是否发生变化？如果变化，请说明理由；如果不变，请求出

\frac{D F}{D E}

的值．

(3)、连接AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．

查看试题解析

备考浙教版中考数学题型专项训练 一次函数解答题专练

一、综合题

备考浙教版中考数学题型专项训练一次函数解答题专练