备考浙教版中考数学题型专项训练一次函数填空题专练

试卷更新日期：2022-05-17 类型：三轮冲刺

进入出卷网下载

一、填空题

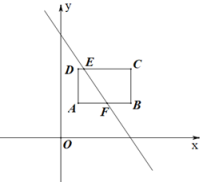
1. 如图，平面直角坐标系中，点A（1，2）、点C（4，4）是矩形ABCD的两个顶点，AB与 $x$ 轴平行，则直线 $y = - \frac{3}{2} x + 6$ 与矩形公共部分的线段EF长为．

查看试题解析
2. 如图，直线L：y=-x+1与坐标轴交于A、B两点，点C是反比例函数 $y = \frac{1}{2 x}$ （x＞0）图象上任意一点，过C分别作横纵轴的垂线CD、CG，交线段AB于E、F两点.设OE=a，EF=b，FA=c，请写出在点C移动过程中，a、b、c保持不变的数量关系.

查看试题解析
3. 如图，在平面直角坐标系中，直线l：y＝ $\frac{\sqrt{3}}{3}$ x﹣ $\sqrt{3}$ 与x轴交于点B₁ ，以OB₁为一边在OB₁上方作等边△A₁OB₁ ，过点A₁作A₁B₂平行于x轴，交直线l于点B₂ ，以A₁B₂为一边在A₁B₂上方作等边△A₂A₁B₂ ，过点A₂作A₂B₃平行于x轴，交直线l于点B₃ ，以A₂B₃为一边在A₂B₃上方作等边△A₃A₂B₃ ， …，则A₂₀₂₀的横坐标是.

查看试题解析
4. 在平面直角坐标系xOy中，直线l：y＝kx﹣1（k ≤ 2）与直线x＝﹣k，y＝﹣k分别交于点A，B．直线x＝﹣k与y＝﹣k交于点C．记线段AB，BC，AC围成的区域（不含边界）为W；横、纵坐标都是整数的点叫做整点．

(1)、当k＝﹣2时，区域W内的整点个数为．

(2)、若区域W内没有整点，则k的取值范围是．

查看试题解析
5. 如图，在平面直角坐标系xOy中，直线l：y= - x-2 交x轴于点A，交y轴于点B，作点A关于y轴的对称点C，D是直线l上的动点，连CD，将CD绕C点逆时针旋转90°至CE。则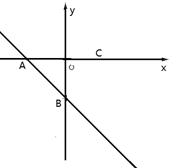

(1)、点C的坐标是

(2)、OE+AE的最小值是.

查看试题解析
6. 如图，在平面直角坐标系中，一次函数y＝－2x＋4的图象与x轴、y轴分别交于点A、B，将直线AB绕点B顺时针旋转45°，交x轴于点C，则直线BC的函数表达式为.

查看试题解析
7. 如图，一次函数 $y = \frac{4}{3}$ x+4的图象与x轴交于点A，与y轴交于点B，C是x轴上的一动点，连接BC，将 $△ A B C$ 沿BC所在的直线折叠，当点A落在y轴上时，点C的坐标为.

查看试题解析
8. 如图，在平面直角坐标系中，直线MN的函数解析式为y＝﹣x+3，点A在线段MN上且满足AN＝2AM，B点是x轴上一点，当△AOB是以OA为腰的等腰三角形时，则B点的坐标为．

查看试题解析
9. 已知点A的坐标是 $(\sqrt{3} ， - 1)$ ，点B是正比例函数 $y = k x (x > 0)$ 的图象上一点，若只存在唯一的点B，使 $△ A O B$ 为等腰三角形，则k的取值范围是.

查看试题解析
10. 若一次函数y=ax+b（a≠0)的图象经过点A(2，3)，且不经过第四象限，则 4a+b的取值范围为.

查看试题解析
11. 如图，平面直角坐标系中，直线 $y = \frac{1}{2} x + 1$ 与 $x$ 轴、 $y$ 轴分别交于 $A$ 、 $B$ 两点，以 $A B$ 为边在第二象限内作正方形 $A B C D$ ，在 $y$ 轴上有一个动点 $M$ ，当 $△ M D C$ 的周长最小的时候，点 $M$ 的坐标是．

查看试题解析
12. 如图，直线 $y = x + 1$ 交x轴于点A，交y轴于点B，点A₁：坐标为(1，0)，过点A₁作x轴的垂线交直线 $y = x + 1$ 于点B₁ ，以点A为圆心，AB₁长为半径画弧交x轴于点A₂；过点A₂作x轴的垂线交直线 $y = x + 1$ 于点B₂ ，以点A为圆心，AB₂长为半径画弧交_x轴于点A₃；……按此做法进行下去，点B₂₀₂₁的坐标为．

查看试题解析
13. 如图，在平面直角坐标系中A（﹣2，1），B（3，4），连接OA、OB、AB ， P是y轴上的一个动点，当|PB﹣PA|取最大值时，点P的坐标为．

查看试题解析
14. 如图，在平面直角坐标系中，函数 $y = \frac{\sqrt{3}}{3} x$ 和 $y = - \sqrt{3} x$ 的图象分别为直线 $l_{1} ， l_{2}$ ，过 $l_{1}$ 上的点 $A_{1} (1 ， \frac{\sqrt{3}}{3})$ 作 $x$ 轴的垂线交 $l_{2}$ 于点 $A_{2}$ ，过点 $A_{2}$ 作 $y$ 轴的垂线交 $l_{1}$ 于点 $A_{3}$ ，过点 $A_{3}$ 作 $x$ 轴的垂线交 $l_{2}$ 于点 $A_{4}$ ，…依次进行下去，则点 $A_{2019}$ 的横坐标为．

查看试题解析
15. 在直角坐标系中，等腰直角三角形A₁B₁O、A₂B₂B₁、A₃B₃B₂、…、A_nB_nB_n﹣1按如图所示放置，其中点A₁、A₂、A₃、…、A_n均在一次函数y=kx+b的图象上，点B₁、B₂、B₃、…、B_n均在x轴上．若点B₁的坐标为（1，0），点B₂的坐标为（3，0），则点A₂₀₁₉的坐标为．

查看试题解析
16. “龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了“龟兔再次赛跑”的故事（x表示乌龟从起点出发所行的时间，y₁表示乌龟所行的路程，y₂表示兔子所行的路程）．有下列说法：①“龟兔再次赛跑”的路程为1000米；②兔子先到达终点；③乌龟比兔子晚出发40分钟；④兔子在760米处追上乌龟．其中正确的说法是．（把你认为正确说法的序号都填上）

查看试题解析
17. 如图，在平面直角坐标系中，将△ABO绕点B顺时针旋转到△A₁BO₁的位置，使点A的对应点A₁落在直线y＝ $\frac{\sqrt{3}}{3}$ x上，再将△A₁BO₁绕点A₁顺时针旋转到△A₁B₁Q₂的位置，使点O₁的对应点O₂落在直线y＝ $\frac{\sqrt{3}}{3}$ x上，依次进行下去…，若点A的坐标是（0，1），点B的坐标是（ $\sqrt{3}$ ， 1），则点A₁₂的横坐标是.

查看试题解析
18. 如图，在平面直角坐标系中，直线 $AB ： y = - x + b$ 交 $y$ 轴于点 $A (0 ， 2)$ ，交 $x$ 轴于点 $B$ ，直线1垂直平分 $OB$ 交 $AB$ 于点 $D$ ，交 $x$ 轴于点 $E$ ，点 $P$ 是直线1上且在第一象限一动点．若 $△ AOP$ 是等腰三角形，点 $P$ 的坐标是．

查看试题解析
19. 如果不论k为何值，一次函数y= $\frac{2 k - 1}{k + 3} x - \frac{k - 11}{k + 3}$ 的图象都经过一定点，则该定点的坐标是．

查看试题解析
20. 如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在一三象限角平分线上，从左向右第3个正方形中的一个顶点A的坐标为（8，4），阴影三角形部分的面积从左向右依次记为S₁、S₂、S₃、…、S_n ，则第4个正方形的边长是， S_n的值为.

查看试题解析
21. 如图所示，从高为2m的点 $A$ 处向右上抛一个小球 $P$ ，小球路线呈抛物线 $L$ 形状，小球水平经过2m时达到最大高度6m，然后落在下方台阶B处弹起，已知 $M N = 4$ m， $F M = D E = B C = 1.2$ m， $C D = E F = 1$ m，若小球弹起形成一条与 $L$ 形状相同的抛物线，且落点 $Q$ 与 $B$ ， $D$ 在同一直线上，则小球弹起时的最大高度是m

查看试题解析
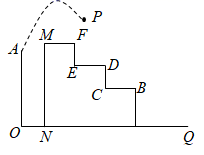22. 如图，点B₁在直线l：y＝ $\frac{1}{2}$ x上，点B₁的横坐标为2，过点B₁作B₁A₁⊥l ，交x轴于点A₁ ，以A₁B₁为边，向右作正方形A₁B₁B₂C₁ ，延长B₂C₁交x轴于点A₂；以A₂B₂为边，向右作正方形A₂B₂B₃C₂ ，延长B₃C₂交x轴于点A₃；以A₃B₃为边，向右作正方形A₃B₃B₄C₃ ，延长B₄C₃交x轴于点A₄；…；照这个规律进行下去，则第n个正方形A_nB_nB_n₊₁C_n的边长为（结果用含正整数n的代数式表示）．

查看试题解析
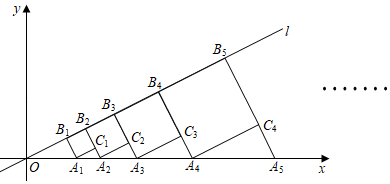23. 已知A、B、C三地顺次在同一直线上，A、C两地相距1400千米，甲乙两车均从A地出发，向B地方向匀速前进，甲车出发5小时后，乙车出发，经过一段时间后两车在B地相遇，甲车到达B地后便在B地卸货，卸完货后从B地按原车速的 $\frac{4}{3}$ 返回A地，而乙车到B地后立刻继续以原速前往C地，到达C地后按原车速的 $\frac{5}{4}$ 原路返回A地，结果甲乙两车同时返回A地，若两车间的距离y（千米）与甲车出发时间x（小时）之间的关系如图所示，则甲车在B地卸货用了小时．

查看试题解析
24. 平面直角坐标系中，已知△ABC的三个顶点分别为A（－1， 0），B（1， 0），C（－3， 2），设△ABC的外心为P，点P到直线y＝ $\sqrt{3}$ x－3的距离为.

查看试题解析
25. 填空

(1)、在平面直角坐标系中，O是坐标原点.过点A（1，2）的直线y=kx+b与x轴交于点B，且△ABO的面积等于4，则k的值为.

(2)、锐角三角形ABC中，∠C=2∠B，AB= $2 \sqrt{6}$ ，BC+CA=8，则△ABC的面积为.

查看试题解析
26. 已知直线y＝﹣2x＋4与x轴，y轴分别交于A、B两点，M是第一象限内的点，若△MAB是以AB为斜边的等腰直角三角形，则M点的坐标是.

查看试题解析
27. 如图所示，以长方形ABCD的边AD的中点为原点建立平面直角坐标系，且AD位于x轴上，AB=CD=2，AD=BC=4，过定点P（0，3）和动点Q（a，0）的直线解析式为y=kx+3，

(1)、若PQ经过点D，则k=

(2)、若PQ与矩形ABCD的边有公共点，且函数y随x的增大而增大，则k的取值范围为

查看试题解析
28. 如图，在平面直角坐标系xOy中，点A坐标为(0，2)，点B为x轴上的动点，以AB为边作等边三角形ABC，当OC最小时点C的坐标为.

查看试题解析
29. 如图，在平面直角坐标系中，点 $N_{1} (1 ， 1)$ 在直线 $l ： y = x$ 上，过点 $N_{1}$ 作 $N_{1} M_{1} ⊥ l$ ，交 $x$ 轴于点 $M_{1}$ ；过点 $M_{1}$ 作 $M_{1} N_{2} ⊥ x$ 轴，交直线 $l$ 于点 $N_{2}$ ；过点 $N_{2}$ 作 $N_{2} M_{2} ⊥ l$ ，交 $x$ 轴于点 $M_{2}$ ；过点 $M_{2}$ 作 $M_{2} N_{3} ⊥ x$ 轴，交直线 $l$ 于点 $N_{3}$ ；…；按此作法进行下去，则点 $M_{2021}$ 的坐标为.

查看试题解析
30. 将正方形A₁B₁C₁A₂ ，A₂B₂C₂A₃ ， A₃B₃C₃A₄ ， ……按如图所示的方式放置，点A₁、A₂、A₃……和点B₁、B₂、B₃ ， ……分别在直线y=x+1和x轴上，则点C₂₀₂₀的纵坐标是

查看试题解析

备考浙教版中考数学题型专项训练 一次函数填空题专练

一、填空题

备考浙教版中考数学题型专项训练一次函数填空题专练