广东省深圳市27校2022年九年级4月联考(二模)数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. -3的绝对值是( )A、-3 B、1 C、3 D、2. 如图所示的几何体是由4个大小相同的小立方块搭成,其主视图是( )
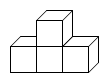 A、
A、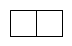 B、
B、 C、
C、 D、
D、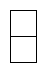 3. 在数轴上表示不等式 的解集正确的是( ).A、
3. 在数轴上表示不等式 的解集正确的是( ).A、 B、
B、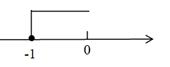 C、
C、 D、
D、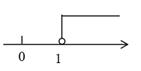 4. 数据2、3、7、8、a的平均数是5,则这组数据的中位数是( )A、4 B、4.5 C、5 D、65. 将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起,若 ,则 的度数为( )
4. 数据2、3、7、8、a的平均数是5,则这组数据的中位数是( )A、4 B、4.5 C、5 D、65. 将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起,若 ,则 的度数为( )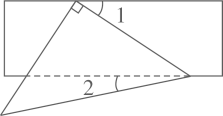 A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 下列尺规作图,能确定AD=BD的是( )A、
A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 下列尺规作图,能确定AD=BD的是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,点A到点C的距离为200米,要测量河对岸B点到河岸 的距离.小明在A点测得B在北偏东 的方向上,在C点测得B在北偏东 的方向上,则B点到河岸 的距离为( )
8. 如图,点A到点C的距离为200米,要测量河对岸B点到河岸 的距离.小明在A点测得B在北偏东 的方向上,在C点测得B在北偏东 的方向上,则B点到河岸 的距离为( ) A、100米 B、200米 C、米 D、 米9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=−1,则下列结论:①abc>0,②a+b<−c,③4a−2b+c>0,④3b+2c<0,⑤a−b<m(am+b)(其中m为任意实数)中正确的个数是( )
A、100米 B、200米 C、米 D、 米9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=−1,则下列结论:①abc>0,②a+b<−c,③4a−2b+c>0,④3b+2c<0,⑤a−b<m(am+b)(其中m为任意实数)中正确的个数是( )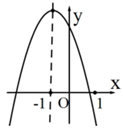 A、2个 B、3个 C、4个 D、5个10. 如图,正方形 中,E、F分别为边 上的点,且 ,过F作 ,交 于G,过H作 于M,若 ,则下列结论中:
A、2个 B、3个 C、4个 D、5个10. 如图,正方形 中,E、F分别为边 上的点,且 ,过F作 ,交 于G,过H作 于M,若 ,则下列结论中:① ;② ;③ ,其中结论正确的是( )
 A、只有①② B、只有①③ C、只有②③ D、①②③
A、只有①② B、只有①③ C、只有②③ D、①②③二、填空题
-
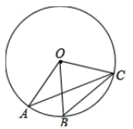
11. 因式分解: .12. 关于x的一元二次方程 的一个根是3,则另一个根是 .13. 如图,A,B,C是 上的三个点, ,则 的度数为 .
 14. 如图,在平面直角坐标系中有 , , ,A(3,0)、C(1, ),将 沿x轴的负方向平移,在第二象限内B、C两点的对应点 、 正好落在反比例函数 的图象上,则 .
14. 如图,在平面直角坐标系中有 , , ,A(3,0)、C(1, ),将 沿x轴的负方向平移,在第二象限内B、C两点的对应点 、 正好落在反比例函数 的图象上,则 .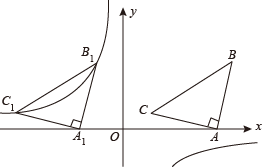 15. 如图,正方形 中, ,点E是对角线 上一点,连接 ,过点E作 ,交 于点F,连接 ,交 于点G,将 沿 翻折,得到 ,连接 ,交 于点N,若 ,则线段 的长是 .
15. 如图,正方形 中, ,点E是对角线 上一点,连接 ,过点E作 ,交 于点F,连接 ,交 于点G,将 沿 翻折,得到 ,连接 ,交 于点N,若 ,则线段 的长是 .
三、解答题
-
16. 先化简,再求值 ,其中 .17. 为了解某校某年级学生一分钟跳绳情况,对该年级全部360名学生进行一分钟跳绳次数的测试,并把测得数据分成四组,绘制成如图所示的频数表和未完成的频数分布直方图(每一组不含前一个边界值,含后一个边界值).
组别(次)
频数
100~130
48
130~160
96
160~190
m
190~220
72
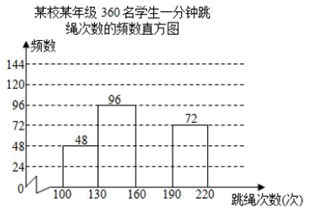 (1)、求m的值;(2)、把频数分布直方图补充完整;(3)、求该年级一分钟跳绳次数在160次以上的学生数占该年级全部学生数的百分比.18. 如图,在单位长度为1的正方形网格中建立直角坐标系,一条圆弧恰好经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
(1)、求m的值;(2)、把频数分布直方图补充完整;(3)、求该年级一分钟跳绳次数在160次以上的学生数占该年级全部学生数的百分比.18. 如图,在单位长度为1的正方形网格中建立直角坐标系,一条圆弧恰好经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号): (1)、利用网格找出该圆弧所在圆的圆心D点的位置,则D点的坐标为;(2)、连接AD、CD,若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为;(3)、连接AB,将线段AB绕点D旋转一周,求线段AB扫过的面积.19. 如图,在 中,点O在斜边 上,以O为圆心, 为半径作圆,分别与BC,AB相交于点D,E,连接 .已知 .
(1)、利用网格找出该圆弧所在圆的圆心D点的位置,则D点的坐标为;(2)、连接AD、CD,若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为;(3)、连接AB,将线段AB绕点D旋转一周,求线段AB扫过的面积.19. 如图,在 中,点O在斜边 上,以O为圆心, 为半径作圆,分别与BC,AB相交于点D,E,连接 .已知 .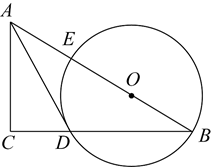 (1)、求证: 是 的切线.(2)、若 ,求 的半径.20. 某地区以移动互联和大数据技术支持智慧课堂,实现学生的自主、个性和多元学习,全区学生逐步实现上课全部使用平板电脑.某公司根据市场需求代理甲,乙两种型号的平板,每台甲型平板比每台乙型平板进价多600元,用6万元购进甲型平板与用4.5万元购进乙型平板的数量相等.(1)、求每台甲型、乙型平板的进价各是多少元?(2)、该公司计划购进甲,乙两种型号的平板共80台进行试销,其中甲型平板为m台,购买资金不超过17.76万元.并且甲型平板不少于乙型平板的2倍,试销时甲型平板每台售价2800元,乙型平板每台售价2400元,问该公司有几种进货方案?并求出这几种方案中,销售完后获得的利润W的最大值.21. 胡老师的数学课上,有这样一道探究题.
(1)、求证: 是 的切线.(2)、若 ,求 的半径.20. 某地区以移动互联和大数据技术支持智慧课堂,实现学生的自主、个性和多元学习,全区学生逐步实现上课全部使用平板电脑.某公司根据市场需求代理甲,乙两种型号的平板,每台甲型平板比每台乙型平板进价多600元,用6万元购进甲型平板与用4.5万元购进乙型平板的数量相等.(1)、求每台甲型、乙型平板的进价各是多少元?(2)、该公司计划购进甲,乙两种型号的平板共80台进行试销,其中甲型平板为m台,购买资金不超过17.76万元.并且甲型平板不少于乙型平板的2倍,试销时甲型平板每台售价2800元,乙型平板每台售价2400元,问该公司有几种进货方案?并求出这几种方案中,销售完后获得的利润W的最大值.21. 胡老师的数学课上,有这样一道探究题.如图,已知 中, ,点P为平面内不与点A、C重合的任意一点,连接 ,将线段 绕点P顺时针旋转 ,得线段 ,连接 点E、F分别为 的中点,设直线 与直线 相交所成的较小角为 ,探究 的值和 的度数与x、y、 的关系.

请您参与学习小组的探究过程,并完成以下任务:
(1)、填空:【问题发现】
小明研究了 时,如图1,求出了 的值和 的度数分别为 , ;
小红研究了 时,如图2,求出了 的值和 的度数分别为 , ;
【类比探究】
他们又共同研究了 时,如图3,也求出了 的值和 的度数;
【归纳总结】
最后他们终于共同探究得出规律: (用含x、y的式子表示); (用含 的式子表示)
(2)、求出 时 的值和 的度数(注:要求写出具体解题过程,否则得零分).22. 如图,已知抛物线C:y=x2+bx+c经过点A(0,−4) ,B(4,0).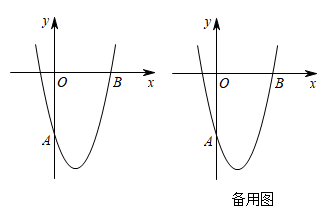 (1)、求b,c的值;(2)、连结AB,交抛物线C的对称轴于点M.
(1)、求b,c的值;(2)、连结AB,交抛物线C的对称轴于点M.①求点M的坐标;
②将抛物线C向左平移m(m>0)个单位得到抛物线C1 . 过点M作MN∥y轴,交抛物线C1于点N.P是抛物线C1上一点,横坐标为−1,过点P作PE∥x轴,交抛物线C于点E,点E在抛物线C对称轴的右侧.若PE+MN= ,求m的值.