广东省揭阳市2022年初中学业水平考试第一次模拟考试数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
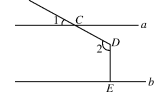
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 新型冠状病毒也叫2019-nCOV,该病毒比细胞小得多,大小约为150nm(纳米),即为0.00000015米,约为一根头发丝直径的千分之一,数据0.00000015米用科学记数法表示为( )A、0.15×10-7米 B、1.5×10-7米 C、1.5×10-8米 D、0.15×10-8米3. 如图,直线a∥b,射线DC与直线a相交于点C,过点D作DE⊥b于点E,已知∠1=25°,则∠2的度数为( )
 A、105° B、115° C、125° D、165°4. 下列运算正确的是( )A、 B、 C、 D、5.
A、105° B、115° C、125° D、165°4. 下列运算正确的是( )A、 B、 C、 D、5.如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
 A、8 B、16 C、10 D、206. 方程|4x-8|+ =0,当y>0时,m的取值范围是( )A、0<m<1 B、m≥2 C、m<2 D、m≤27. 如图,在正方体中,沿对角线BD和顶点A所在的平面截出几何体A﹣BCD,则这个几何体的展开图可能是( )
A、8 B、16 C、10 D、206. 方程|4x-8|+ =0,当y>0时,m的取值范围是( )A、0<m<1 B、m≥2 C、m<2 D、m≤27. 如图,在正方体中,沿对角线BD和顶点A所在的平面截出几何体A﹣BCD,则这个几何体的展开图可能是( ) A、
A、 B、
B、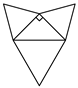 C、
C、 D、
D、 8. 已知二次函数 的顶点为(1,5),那么关于x的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定9. 为了能让更多人接种,某药厂的新冠疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前5天按原计划的速度生产,5天后以原来速度的1.25倍生产,结果比原计划提前3天完成任务.设原计划每天生产 万支疫苗,则可列方程为( )A、 B、 C、 D、10. 如图, 是⊙O的直径, 的平分线交⊙O于点 ,连接 , ,给出下列四个结论:① ;② 是等腰直角三角形;③ ;④ .其中正确的结论是( )
8. 已知二次函数 的顶点为(1,5),那么关于x的一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定9. 为了能让更多人接种,某药厂的新冠疫苗生产线开足马力,24小时运转,该条生产线计划加工320万支疫苗,前5天按原计划的速度生产,5天后以原来速度的1.25倍生产,结果比原计划提前3天完成任务.设原计划每天生产 万支疫苗,则可列方程为( )A、 B、 C、 D、10. 如图, 是⊙O的直径, 的平分线交⊙O于点 ,连接 , ,给出下列四个结论:① ;② 是等腰直角三角形;③ ;④ .其中正确的结论是( ) A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. 数据:3、5、4、5、2、3的中位数是 .12. 分解因式: .13. 抛物线 关于x轴对称的抛物线的解析式是 .14. 不等式组 的解集是 .15. 如图,分别以等边三角形的三个顶点为圆心,以边长为半径画弧,得到的封闭图形叫作莱洛三角形,若 , 则莱洛三角形的面积(即阴影部分面积)为 .
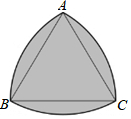 16. 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为 .
16. 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为 . 17. 如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,PM=l,则l的最大值是
17. 如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点C作CP⊥AB于点P,若CD=3,AB=8,PM=l,则l的最大值是
三、解答题
-
18. 小颖用下面的方法求出方程 的解.
方程
换元法得新方程
解新方程
检验
求原方程的解
令 ,则
,所以
请你仿照小颗的方法求出方程 的解.
19. 如图,已知点E、C在线段BF上,且BE=CF,CM∥DF, (1)、作图:在BC上方作射线BN,使∠CBN=∠1,交CM的延长线于点A(用尺规作图法,保留作图痕迹,不写作法);(2)、在(1)的条件下,求证:AC=DF.20. 2022年冬奥会吉祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”,如图,现有三张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中两张正面印有冰墩墩图案的卡片分别记为A1、A2 , 正面印有雪容融图案的卡片记为B,将三张卡片正面向下洗匀,小明同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片.(1)、从这三张卡片中随机挑选一张,是“冰墩墩”的概率是;(2)、请用画树状图或列表的方法,求小明同学抽出的两张卡片都是冰墩墩卡片的概率.
(1)、作图:在BC上方作射线BN,使∠CBN=∠1,交CM的延长线于点A(用尺规作图法,保留作图痕迹,不写作法);(2)、在(1)的条件下,求证:AC=DF.20. 2022年冬奥会吉祥物为“冰墩墩”,冬残奥会吉祥物为“雪容融”,如图,现有三张正面印有吉祥物的不透明卡片,卡片除正面图案不同外,其余均相同,其中两张正面印有冰墩墩图案的卡片分别记为A1、A2 , 正面印有雪容融图案的卡片记为B,将三张卡片正面向下洗匀,小明同学从中随机抽取一张卡片,记下图案后正面向下放回,洗匀后再从中随机抽取一张卡片.(1)、从这三张卡片中随机挑选一张,是“冰墩墩”的概率是;(2)、请用画树状图或列表的方法,求小明同学抽出的两张卡片都是冰墩墩卡片的概率. 21. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD , BC交于M , N两点,连接CM , AN .
21. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD , BC交于M , N两点,连接CM , AN .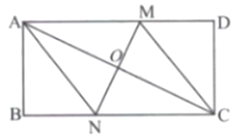 (1)、求证:四边形ANCM为平行四边形;(2)、若AD=4,AB=2,且MN⊥AC , 求DM的长.22. 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数 的图象交AB于E点,连接DE.若OD=5, .
(1)、求证:四边形ANCM为平行四边形;(2)、若AD=4,AB=2,且MN⊥AC , 求DM的长.22. 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数 的图象交AB于E点,连接DE.若OD=5, . (1)、求过点D的反比例函数的解析式;(2)、求 的面积;(3)、x轴上是否存在点P使△OPD为直角三角形,请直接写出P点的坐标.23. 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,OB与y轴相交于另一点G.
(1)、求过点D的反比例函数的解析式;(2)、求 的面积;(3)、x轴上是否存在点P使△OPD为直角三角形,请直接写出P点的坐标.23. 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,OB与y轴相交于另一点G. (1)、求证:BC是⊙F的切线;(2)、若点A、D的坐标分别为A(0,-1),D(2,0),求 的半径;(3)、求证:AF= AD+CD.24. 火炬村在推进美丽乡村建设中,决定建设“火炬幸福广场”,计划铺设相同大小、规格的红色和蓝色地砖,经过调查,获取信息如下表:
(1)、求证:BC是⊙F的切线;(2)、若点A、D的坐标分别为A(0,-1),D(2,0),求 的半径;(3)、求证:AF= AD+CD.24. 火炬村在推进美丽乡村建设中,决定建设“火炬幸福广场”,计划铺设相同大小、规格的红色和蓝色地砖,经过调查,获取信息如下表:类别
购买数量低于500块
购买数量不低于500块
红色地砖
原价销售
以八折销售
蓝色地砖
原价销售
以九折销售
若购买红色地砖400块,蓝色地砖600块,需付款8600元;若购买红色地砖1000块,蓝色地砖350块,需付款9900元.
(1)、红色地砖和蓝色地砖的单价各多少元?(2)、经过测算,现需要购置地砖1200块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过600块,如何购买花费最少?最少是多少元?请说明理由.25. 如图,已知抛物线 (a≠0)与x轴交于点A(-1,0),B(4,0),与y轴交于点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q. (1)、求抛物线的解析式;(2)、当点P在线段OB上运动时,直线l交直线BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(3)、点P在线段AB上运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由
(1)、求抛物线的解析式;(2)、当点P在线段OB上运动时,直线l交直线BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(3)、点P在线段AB上运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由