广东省广州市增城区2022年九年级中考一模数学试题

试卷更新日期：2022-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 实数 $- 5$ 的绝对值是（）

A、 $\sqrt{5}$ B、5 C、0 D、±5

查看试题解析
2. 下列正多边形中，对称轴最多的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、 $2 a + 5 b = 10 a b$ B、 $x^{2} \cdot x^{3} = x^{6}$ C、 ${(m^{2} n)}^{3} = m^{5} n^{4}$ D、 $12 m^{2} n \div 3 m n = 4 m$

查看试题解析
4. 平面直角坐标系中，⊙O的圆心在原点，半径为5，则点 $P (0 ， 4)$ 与⊙O的位置关系是（　　）

A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法确定

查看试题解析
5. 一组数据2，4，5，3，2的中位数是（）

A、5 B、3.5 C、3 D、2.5

查看试题解析
6. 一种药品原价每盒25元经过两次降价后每盒16元．设两次降价的百分率都相同为 $x$ ，则 $x$ 满足方程（）

A、 $25 (1 - 2 x^{2}) = 16$ B、 $25 {(1 - x)}^{2} = 16$ C、 $16 (1 + 2 x^{2}) = 25$ D、 $16 (1 + x^{2}) = 25$

查看试题解析
7. 如图，一辆小车沿倾斜角为α的斜坡向上行驶13m，若sinα $= \frac{5}{13}$ ，则小车上升的高度是（）

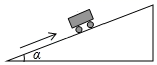A、5m B、6m C、6.5m D、12m

查看试题解析
8. 如图，在△ABC中，AB=AC=8，AD是角平分线，BE是中线，则DE的长为（）

A、3 B、4 C、5 D、6

查看试题解析
9. 如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连接OD，若∠C=50°，则∠AOD的度数为（）

A、40° B、50° C、70° D、80°

查看试题解析
10. 如图，直线y= $\frac{2}{3}$ x+2分别与x轴、y轴交于点A、B，以线段AB为边，在第二象限内作等腰直角ΔABC，∠BAC=90°，则直线BC的解析式为（）

A、 $y = \frac{1}{3} x + 2$ B、 $y = - \frac{1}{4} x + 2$ C、 $y = - \frac{1}{5} x + 2$ D、 $y = - 2 x + 2$

查看试题解析

二、填空题

11. 不等式 $x + 1 < 2$ 的解集是．

查看试题解析
12. 分解因式： $a^{2} - 1$ =.

查看试题解析
13. 一个圆锥的母线长为3，底面的半径为1，则该圆锥的侧面积为．（结果保留π）

查看试题解析
14. 如图，点E是矩形 $A B C D$ 边上一点， $E F ⊥ A C$ 于点F ，若 $\tan ∠ B A C = 2 ， E F = 3$ ，则 $A F$ 的长为．

查看试题解析
15. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90^{\circ}$ ， $A C = 8 ， B C = 15$ ，将 $Δ A B C$ 绕点 $B$ 顺时针旋转60°，得到 $Δ E B D$ ，连接 $D C$ 交 $A B$ 于点 $F$ ，则 $Δ A C F$ 与 $Δ B D F$ 的周长之和为．

查看试题解析
16. 如图，点 $P$ 是正方形 $A B C D$ 的对角线 $B D$ 延长线上的一点，连接 $P A$ ，过点 $P$ 作 $P E ⊥ P A$ 交 $B C$ 的延长线于点 $E$ ，过点 $E$ 作 $E F ⊥ B P$ 于点 $F$ ，则下列结论中，正确的是．（填写所有正确结论的序号）
① $P A = P E$ ；② $C E = \sqrt{2} P D$ ；③ $B F - P D = \frac{1}{2} B D$ ；④ $S_{Δ P E F} = S_{Δ A D P}$ ．

查看试题解析

三、解答题

17. 解方程组： ${\begin{array}{l} x - y = 1 \\ 2 x + y = 5 \end{array}$

查看试题解析
18. 如图，菱形ABCD中，DM⊥AB于点M，DN⊥BC于点N．求证：AM=CN．

查看试题解析
19. 已知A＝（a﹣ $\frac{a^{2}}{a + b}$ ）÷ $\frac{a^{2} b^{2}}{a^{2} - b^{2}}$ ．

(1)、化简A；

(2)、若点P（a，b）是直线y＝x﹣2与反比例函数y＝ $\frac{1}{x}$ 的图象的交点，求A的值．

查看试题解析
20. 2022年2月4日，北京冬奥会正式拉开帷幕，小明同学非常喜欢冰球、短道速滑、自由式滑雪、冰壶、花样滑冰这五个项目，他也想知道大家对这五个项目的喜爱程度，于是他对所在小区的居民做了一次随机调查统计，让每个人在这五个项目中选一项最喜欢的，并根据这个统计结果制作了如下两幅不完整的统计图：（其中A冰球、B短道速滑、C自由式滑雪、D冰壶、E花样滑冰）

(1)、请补全条形统计图；

(2)、由于小明同学能够观看比赛的时间有限，所以他只能从这五个项目中随机选两个项目观看，用列举法求小明选到项目B，C的概率．

查看试题解析
21. 如图，已知反比例函数 $y = \frac{k^{2} + 1}{x}$ （ $k$ 为常数）．

(1)、点 $P_{1} (- 1 ， y_{1}) 、 P_{2} (- 2 ， y_{2})$ 为该反比例函数图象上的两点，直接写出 $y_{1}$ 和 $y_{2}$ 的大小关系；

(2)、设点 $P (m ， n) (m > 0)$ 是图象上的一点，过点 $P$ 作 $P M ⊥ x$ 轴于点 $M$ ． $O$ 为坐标原点，若 $\tan ∠ P O M = 2$ ， $P O = \sqrt{5}$ ．求 $k$ 的值并直接写出不等式 $k x - \frac{k^{2} + 1}{x} > 0$ 的解集．

查看试题解析
22. 为了配合学校贯彻落实“双减”政策，开展学生课后体育活动，某体育用品商店用10000元购进了一批足球，很快销售一空；商店又用10000元购进了第二批该种足球，每个足球的进价比原来小涨了25%，结果所购进足球的数量比第一批少40个．

(1)、求第一批足球每个的进价是多少元？

(2)、若商店将第一批足球以售价70元，第二批足球以售价80元全部售出，则其盈利多少元？

查看试题解析
23. 如图，在 $Δ A B C$ 中， $A B = A C$ ．

(1)、尺规作图：以 $A B$ 为直径作 $⊙ O$ 交 $B C$ 于点 $D$ ，交 $A C$ 于点 $E$ ．（保留作图痕迹，不写作法）

(2)、在（1）所作的图中，
①连接 $B E 、 O D$ ，求证： $O D ⊥ B E$ ；

②设 $O D 、 B E$ 相交于点 $F$ ，若 $\frac{C E}{O F} = \frac{2}{3}$ ，求 $\frac{A C}{B C}$ 的值．

查看试题解析
24. 已知抛物线 $y = x^{2} + 6 m x + 9 m^{2} - 6 m - 8$ 的顶点为 $P$ ．

(1)、当 $m = 1$ 时，求点 $P$ 的坐标；

(2)、经过探究发现，随着 $m$ 的变化，顶点 $P$ 在某直线 $l$ 上运动，直线 $l$ 与 $x$ 轴， $y$ 轴分别交于 $A$ ， $B$ 两点，求 $△ A O B$ 的面积；

(3)、若抛物线与直线 $l$ 的另一交点为 $Q$ ，以 $P Q$ 为直径的圆与坐标轴相切，求 $m$ 的值．

查看试题解析
25. 如图1，在平面直角坐标系xOy中，点A的坐标为（5，0），点B在第一象限内，且使得AB = 4，OB = 3．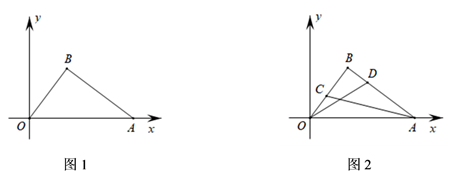

(1)、试判断△AOB的形状，并说明理由；

(2)、在第二象限内是否存在一点P，使得△POB是以OB为腰的等腰直角三角形，若存在，求出点P的坐标：若不存在，请说明理由；

(3)、如图2，点C为线段OB上一动点，点D为线段BA上一动点，且始终满足OC = BD．求AC + OD的最小值．

查看试题解析