备考浙教版中考数学题型专项训练 一次函数选择题专练
试卷更新日期:2022-05-17 类型:三轮冲刺
一、单选题
-
1. 如图,直线y=﹣x+4分别与x轴、y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( )
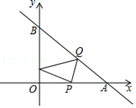 A、(2,2) B、(2.5,1.5) C、(3,1) D、(1.5,2.5)2. 在平面直角坐标系中,已知直线l1:y=-2x+4交y轴于点A,若l1关于y轴的对称直线为l2 , 直线l2的有一个点M ,当M 点到直线l1的距离小于 ,则点M 的横坐标m取值范围是( )A、-2<m<2 B、-1.75<m<1.75 C、-1.5<m<1.5 D、-1.25<M<1.253. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行3600米,先到终点的人原地休息.已知甲先出发6分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,以下结论:①甲步行的速度为60米/分;②乙走完全程用了48分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有1200米.其中正确的结论有( )
A、(2,2) B、(2.5,1.5) C、(3,1) D、(1.5,2.5)2. 在平面直角坐标系中,已知直线l1:y=-2x+4交y轴于点A,若l1关于y轴的对称直线为l2 , 直线l2的有一个点M ,当M 点到直线l1的距离小于 ,则点M 的横坐标m取值范围是( )A、-2<m<2 B、-1.75<m<1.75 C、-1.5<m<1.5 D、-1.25<M<1.253. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行3600米,先到终点的人原地休息.已知甲先出发6分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,以下结论:①甲步行的速度为60米/分;②乙走完全程用了48分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有1200米.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个4. 小明同学利用周末从家里出发骑自行车到某小区参加志愿服务活动、活动结束后原路返回家中,他离家的距离y(千米)与时间x(小时)之间的函数图象如图中折线所示,若 , 小明返回时骑行的平均速度是前往某小区时的平均速度的 , 根据图中数据,下列结论中,正确的结论的是( )
A、1个 B、2个 C、3个 D、4个4. 小明同学利用周末从家里出发骑自行车到某小区参加志愿服务活动、活动结束后原路返回家中,他离家的距离y(千米)与时间x(小时)之间的函数图象如图中折线所示,若 , 小明返回时骑行的平均速度是前往某小区时的平均速度的 , 根据图中数据,下列结论中,正确的结论的是( )①某小区离小明家12千米;②小明前往某小区时,中途休息了0.25小时;
③小明前往某小区时的平均速度是16千米/小时;
④小明在某小区志愿服务的时间为1小时;⑤a的值为 .
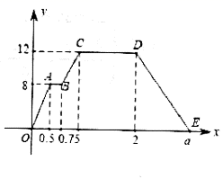 A、2个 B、3个 C、4个 D、5个5. 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
A、2个 B、3个 C、4个 D、5个5. 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( ) A、1.4 B、2.5 C、2.8 D、36. 对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )
A、1.4 B、2.5 C、2.8 D、36. 对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )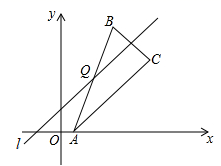 A、12 B、14 C、16 D、187. 正方形A1B1C1O、A2B2C2C1、A3B3C3C2 . ..按如图所示放置,点A1 , A2 , A3和点C1 , C2 , C3 . ..,分别在直线y=kx+b(k>0)和x轴上,已知点B1 , B2 , B3 , B4的坐标分别为(1,1),(3,2),(7,4),(15,8),则Bn的坐标是( )
A、12 B、14 C、16 D、187. 正方形A1B1C1O、A2B2C2C1、A3B3C3C2 . ..按如图所示放置,点A1 , A2 , A3和点C1 , C2 , C3 . ..,分别在直线y=kx+b(k>0)和x轴上,已知点B1 , B2 , B3 , B4的坐标分别为(1,1),(3,2),(7,4),(15,8),则Bn的坐标是( )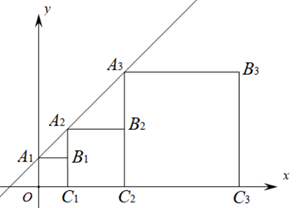 A、(2n-1,2n-1) B、(2n , 2n-1) C、(2n-1 , 2n) D、(2n-1 , 2n-1)8. 如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( )
A、(2n-1,2n-1) B、(2n , 2n-1) C、(2n-1 , 2n) D、(2n-1 , 2n-1)8. 如图,抛物线G:y1=a(x+1)2+2与H:y2=﹣(x﹣2)2﹣1交于点B(1,﹣2),且分别与y轴交于点D、E.过点B作x轴的平行线,交抛物线于点A、C,则以下结论:①无论x取何值,y2总是负数;②抛物线H可由抛物线G向右平移3个单位,再向下平移3个单位得到;③当﹣3<x<1时,随着x的增大,y1﹣y2的值先增大后减小;④四边形AECD为正方形.其中正确的是( ) A、①③④ B、①②④ C、②③④ D、①②③④9. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、810. 小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 ,其中 ,则他探究这7条直线的交点个数最多是( )A、17个 B、18个 C、19个 D、21个11. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、412. 一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
A、①③④ B、①②④ C、②③④ D、①②③④9. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、810. 小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线 ,其中 ,则他探究这7条直线的交点个数最多是( )A、17个 B、18个 C、19个 D、21个11. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、412. 一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:会员年卡类型
办卡费用/元
每次游泳收费/元
A类
50
25
B类
200
20
C类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550(元),若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A、购买A类会员年卡 B、购买B类会员年卡 C、购买C类会员年卡 D、不购买会员年卡13. 若实数a,b,c满足 =k,则直线y=kx+k必经过第几象限( )A、一、二、三 B、一、三 C、二、三 D、二、四14. 如图,在平面直角坐标系中,四边形 ,…都是菱形,点 …都在x轴上,点 ,…都在直线 上,且 ,则点 的横坐标是( )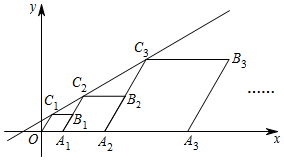 A、 B、 C、 D、15. 在A、B两地之间有汽车站C(C在直线上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶;甲、乙两车离C站的距离 , (千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇;其中正确的结论有( )
A、 B、 C、 D、15. 在A、B两地之间有汽车站C(C在直线上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶;甲、乙两车离C站的距离 , (千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距360千米;②甲车速度比乙车速度快15千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇;其中正确的结论有( )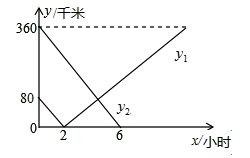 A、1 B、2个 C、3个 D、4个16. 牛奶配送员小吴从县城出发,骑配送车到米村配送牛奶,途中遇到在县城上学的外甥张聪从米村步行返校上学,小吴在米村配送牛奶后,在返回县城途中又遇到张聪,便用配送车载上张聪一起返回县城,结果小吴比预计时间晚到5分钟,二人与县城间的距离y(km)和小吴从县城出发后所用时间x(min)之间的关系如图,假设两人之间的交流时间忽略不计,则下列说法正确的有( )个.
A、1 B、2个 C、3个 D、4个16. 牛奶配送员小吴从县城出发,骑配送车到米村配送牛奶,途中遇到在县城上学的外甥张聪从米村步行返校上学,小吴在米村配送牛奶后,在返回县城途中又遇到张聪,便用配送车载上张聪一起返回县城,结果小吴比预计时间晚到5分钟,二人与县城间的距离y(km)和小吴从县城出发后所用时间x(min)之间的关系如图,假设两人之间的交流时间忽略不计,则下列说法正确的有( )个.①小吴到达米村后配送牛奶所用时间为25min;②小吴从县城出发,最后回到县城用时100min;③两人第一次相遇时,小吴距离米村2km;④张聪从米村到县城步行速度为0.05km/min.
 A、1 B、2 C、3 D、417. 如图,折线表示一骑车人离家的距离 与时间 的关系,骑车人9:00离开家,15:00回到家,则下列说法错误的是( )
A、1 B、2 C、3 D、417. 如图,折线表示一骑车人离家的距离 与时间 的关系,骑车人9:00离开家,15:00回到家,则下列说法错误的是( )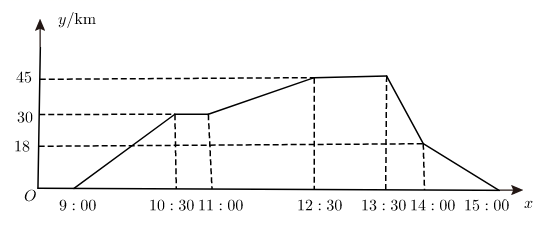 A、骑车人离家最远距离是45km B、骑车人中途休息的总时间长是1.5h C、从9:00到10:30骑车人离家的速度越来越大 D、骑车人返家的平均速度是30km/h18. 函数y= x﹣3的图象与x轴、y轴分别交于A、B两点,点C在x轴上.若△ABC为等腰三角形,则满足条件的点C共有( )A、4个 B、3个 C、2个 D、1个19. 如图,已知反比例函数 (k≠0)的图象经过矩形ABCD的对角线AC的端点A和C,AC交y轴于点F,BC边交y轴于点E,过线段FO中点G的直线与AC平行,连接AE,若∠BAE=∠ACB, . 则k的值为( )
A、骑车人离家最远距离是45km B、骑车人中途休息的总时间长是1.5h C、从9:00到10:30骑车人离家的速度越来越大 D、骑车人返家的平均速度是30km/h18. 函数y= x﹣3的图象与x轴、y轴分别交于A、B两点,点C在x轴上.若△ABC为等腰三角形,则满足条件的点C共有( )A、4个 B、3个 C、2个 D、1个19. 如图,已知反比例函数 (k≠0)的图象经过矩形ABCD的对角线AC的端点A和C,AC交y轴于点F,BC边交y轴于点E,过线段FO中点G的直线与AC平行,连接AE,若∠BAE=∠ACB, . 则k的值为( )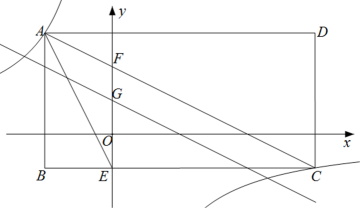 A、-24 B、-16 C、-36 D、-1220. 如图,一次函数 的图象与 轴、 轴分别相交于点 、 ,点 在反比例函数 的图象上.若 是等腰直角三角形,则下列 的值错误的是( )
A、-24 B、-16 C、-36 D、-1220. 如图,一次函数 的图象与 轴、 轴分别相交于点 、 ,点 在反比例函数 的图象上.若 是等腰直角三角形,则下列 的值错误的是( )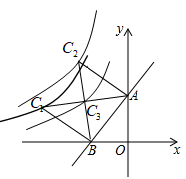 A、-28 B、-21 C、-14 D、21. 如图,在平面直角坐标系中,直线 分别与 轴、 轴交于 , 两点,在线段 上取一点 ,过 作 轴于 , 轴于 ,连结 ,当 最短时,点 的坐标为( )
A、-28 B、-21 C、-14 D、21. 如图,在平面直角坐标系中,直线 分别与 轴、 轴交于 , 两点,在线段 上取一点 ,过 作 轴于 , 轴于 ,连结 ,当 最短时,点 的坐标为( )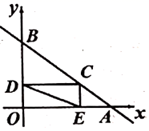 A、 B、 C、 D、22. 已知点 在经过原点的一条直线l上,且 ,则 的值为( )A、 B、 C、0 D、-123. 直角坐标系 中,一次函数 的图象过点 ,且 ,与 轴, 轴分别交于 , 两点.设 的面积为 ,则 的最小值是( )A、4 B、3 C、2 D、124. 如图,在平面直角坐标系中,若折线 与直线交 ( )有且仅有一个交点,则 的取值范围是( )
A、 B、 C、 D、22. 已知点 在经过原点的一条直线l上,且 ,则 的值为( )A、 B、 C、0 D、-123. 直角坐标系 中,一次函数 的图象过点 ,且 ,与 轴, 轴分别交于 , 两点.设 的面积为 ,则 的最小值是( )A、4 B、3 C、2 D、124. 如图,在平面直角坐标系中,若折线 与直线交 ( )有且仅有一个交点,则 的取值范围是( )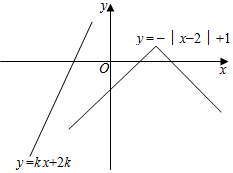 A、 或 B、 或 C、 或 D、 或25. 如图,在平面直角坐标系中, 斜边 中点与原点 重合, 点是平面内第二象限内一点,且 平分 ,连接 ,反比例函数 的图象经过 两点.已知 两点横坐标分别为 的面积为 ,则 的值为( )
A、 或 B、 或 C、 或 D、 或25. 如图,在平面直角坐标系中, 斜边 中点与原点 重合, 点是平面内第二象限内一点,且 平分 ,连接 ,反比例函数 的图象经过 两点.已知 两点横坐标分别为 的面积为 ,则 的值为( )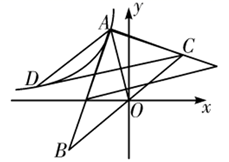 A、 B、-4 C、 D、-226. A、B两地相距80km,甲、乙两人沿同一条路从A地到B地。I1 , l2分别表示甲、乙两人离开A地的距离s(kxm)与时间t(h)之间的关系。对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是 km/h;④当乙车出发2小时时,两车相距13km。其中正确的结论是( )
A、 B、-4 C、 D、-226. A、B两地相距80km,甲、乙两人沿同一条路从A地到B地。I1 , l2分别表示甲、乙两人离开A地的距离s(kxm)与时间t(h)之间的关系。对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是 km/h;④当乙车出发2小时时,两车相距13km。其中正确的结论是( ) A、①③ B、①④ C、②③ D、②④27. 如图,在平面直角坐标系中,直线l为正比例函数 的图象,点 的坐标为 ,过点 作x轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线l的垂线,垂足为 ,交x轴于点 ,以 为边作正方形 ;过点 作x轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是( )
A、①③ B、①④ C、②③ D、②④27. 如图,在平面直角坐标系中,直线l为正比例函数 的图象,点 的坐标为 ,过点 作x轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线l的垂线,垂足为 ,交x轴于点 ,以 为边作正方形 ;过点 作x轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是( )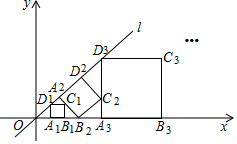 A、 B、 C、 D、28. 如图,在平面直角坐标系中,O为坐标原点,四边形 的顶点A、B、C的坐标分别为(3,0)、(0,1)、(3,3).点P在折线 上,连结 ,交函数 的图象于点Q.若 ,则k的取值范围是( )
A、 B、 C、 D、28. 如图,在平面直角坐标系中,O为坐标原点,四边形 的顶点A、B、C的坐标分别为(3,0)、(0,1)、(3,3).点P在折线 上,连结 ,交函数 的图象于点Q.若 ,则k的取值范围是( )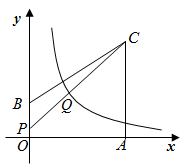 A、 B、 C、 D、29. 如图,在反比例函数 的图象上有动点A,连接OA, 的图象经过OA的中点B,过点B作BC∥x轴交函数 的图象于点C,过点C作CE∥y轴交函数 的图象于点D,交x轴点E,连接AC,OC,BD,OC与BD交于点F.下列结论:①k=1;② ;③ ,④若BD=AO,则∠AOC=2∠COE.其中正确的是( )
A、 B、 C、 D、29. 如图,在反比例函数 的图象上有动点A,连接OA, 的图象经过OA的中点B,过点B作BC∥x轴交函数 的图象于点C,过点C作CE∥y轴交函数 的图象于点D,交x轴点E,连接AC,OC,BD,OC与BD交于点F.下列结论:①k=1;② ;③ ,④若BD=AO,则∠AOC=2∠COE.其中正确的是( )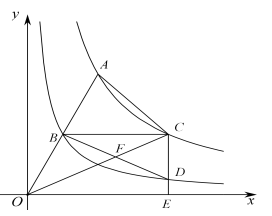 A、①③④ B、②③④ C、①②④ D、①②③④30. 如图,以矩形 的顶点 为圆心,适当长为半径作弧,分别交 , 于点 , ;再分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ;作射线 ,交 于点 ,连接 ,交 于点 .若 , ,则 的长为( )
A、①③④ B、②③④ C、①②④ D、①②③④30. 如图,以矩形 的顶点 为圆心,适当长为半径作弧,分别交 , 于点 , ;再分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ;作射线 ,交 于点 ,连接 ,交 于点 .若 , ,则 的长为( )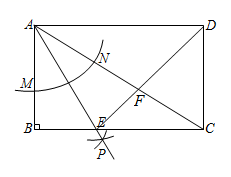 A、1 B、 C、 D、
A、1 B、 C、 D、