广东省广州市越秀区2022年九年级数学一模试题

试卷更新日期：2022-05-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列四个选项中，最小的数是（）

A、- π B、0 C、|- 6| D、3

查看试题解析
2. 神舟十三号飞船在太空中以约每小时28440千米的速度飞行，每90分钟绕地球一圈．将28440用科学记数法表示应为（）

A、 $28.44 \times 10^{3}$ B、 $2.844 \times 10^{4}$ C、 $2.844 \times 10^{5}$ D、 $0.2844 \times 10^{5}$

查看试题解析
3. 下列运算正确的是（）.

A、 $\sqrt{4} = \pm 2$ B、 $a^{9} \div a^{3} = a^{3}$ C、（a+b）² = a² + b² D、2a²b - ba² = a²b

查看试题解析
4. 若点A（1， $y_{1}$ ），B（2， $y_{2}$ ）在反比例函数 $y = \frac{6}{x}$ 的图象上．则 $y_{1}$ ， $y_{2}$ 的大小关系是（）．

A、 $y_{2} < 0 < y_{1}$ B、 $0 < y_{2} < y_{1}$ C、 $y_{1} < 0 < y_{2}$ D、 $y_{1} < y_{2} < 0$

查看试题解析
5. 如图，菱形ABCO的顶点O为⊙O的圆心，顶点A，B，C均在圆周上，则∠A的度数是（）

A、30° B、45° C、60° D、75°

查看试题解析
6. 今年3月份某校举行学雷锋志愿服务活动，为了解学生一周学雷锋志愿服务的次数、随机抽取了50名学生进行一周学雷锋志愿服务次数调查，依据调查结果绘制了如图的折线统计图．下列有关该校一周学雷锋志愿服务次数说法正确的是（）

A、众数是5 B、众数是13 C、中位数是7 D、中位数是9

查看试题解析
7. 根据统计数据提示：广州市2019年地区生产总值为2.36万亿元，2021年地区生产总值为2.82万亿元如果广州市地区生产总值的年平均增长率为x，那么下列方程正确的是（）

A、2.36（l + x） = 2.82 B、2.36（1 + 2x） = 2.82 C、 $2.36 {(1 + 2 x)}^{2} = 2.82$ D、2.36（1+x）² = 2.82

查看试题解析
8. 如图，在Rt△ABC中，∠ACB = 90°，CE是斜边AB上的中线，BD⊥CE于点D，过点A作AF⊥CE交CE延长线于点F．下列结论不一定成立的是（）

A、∠BAC = ∠DBC B、tan ∠ECB $= \frac{A C}{B C}$ C、AF = BD D、CE = CB

查看试题解析
9. 将正方形ABCD与正方形BEFG按如图方式放置，点F、B、C在同一直线上．已知BG = $\sqrt{2}$ ，BC = 3，连接DF．M是DF的中点，连接AM，则AM的长是（）

A、 $\frac{\sqrt{10}}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{13}}{2}$ D、 $\frac{3}{2}$

查看试题解析
10. 已知二次函数 $y = a x^{2} + 4 a x + c$ （a<0）的图象经过A（ - 5， $y_{1}$ ），B（-3， $y_{2}$ ），C（0， $y_{3}$ ）．D（2， $y_{4}$ ）四个点．下列说法一定正确的是（）．

A、若 $y_{1} y_{2} > 0$ ，则 $y_{3} y_{4} > 0$ B、若 $y_{1} y_{4} > 0$ ，则 $y_{2} y_{3} > 0$ C、若 $y_{2} y_{4} > 0$ ，则 $y_{1} y_{3} > 0$ D、若 $y_{3} y_{4} > 0$ ，则 $y_{1} y_{2} > 0$

查看试题解析

二、填空题

11. 使 $\sqrt{x - 1}$ 在实数范围内有意义的 $x$ 应满足的条件是．

查看试题解析
12. 如图，若直线 $l_{1}$ // $l_{2}$ ， $l_{3}$ 是截线，∠1 = 32°，则∠3的度数是．

查看试题解析
13. 已知一个圆锥的底面直径是10厘米，高是12厘米，则该圆锥的侧面积是平方厘米．（结果保留π）

查看试题解析
14. 若关于x的一元二次方程（a - 1）x² - ax + a² = 1的一个根为0．则a = ．

查看试题解析
15. 如果一次函数y = kx + b（k≠0）中两个变量x，y的部分对应值如下表所示：那么关于x的不等式kx + b≥8的解集是．

x

$\dots$

-3

-2

-1

0

1

$\dots$

y

$\dots$

11

8

5

2

-1

$\dots$

查看试题解析
16. 如图，点E为矩形ABCD的边BC上一点（点E与点B不重合），AB = 6，AD = 8，将△ABE沿AE对折，得到△AFE，连接DF，CF．给出下列四个结论：①∠BAF与∠BEF互补；②若点F到边AD、BC的距离相等．则sin∠BAE = $\frac{1}{2}$ ；③若点F到边AB、CD的距离相等．则tan∠BAE = $\frac{1}{2}$ ；④△CDF的面积的最小值为6．其中正确的结论有．（填写所有正确结论的序号）

查看试题解析

三、解答题

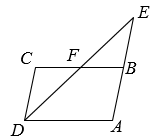
17. 解不等式组： ${\begin{matrix} 2 x - 1 \leq x + 2 \\ x < 2 x - 2 \end{matrix}$

查看试题解析
18. 如图，四边形ABCD是平行四边形，延长AB至点E．使BE = AB．连接DE交BC于点F．求证：CF = BF．

查看试题解析
19. 已知 $A = \frac{2 m + n}{m^{2} - 2 m n + n^{2}} \div \frac{m + n}{m^{2} - n^{2}}$ ．

(1)、化简A；

(2)、若点P（m，n）是直线y =- 2x + 5与y = x - 1的交点，求A的值．

查看试题解析
20. 2022年2月6日晚，中国女足在第20届亚洲杯决赛中以3：2逆转夺冠！全国各地掀起了一股学女足精神的热潮．某学校准备购买一批足球，第一次用3000元购进A类足球若干个，第二次又用3000元购进B类足球，购进数量比第一次多了20个．已知A类足球的单价是B类足球单价的1.5倍．

(1)、求B类足球的单价是多少元；

(2)、若学校需采购A，B两类足球共200个，总费用不超过12000元，则A类足球最多购买多少个？

查看试题解析

21. 某班以“我最喜欢的冰雪运动项目”为主题对全班学生进行随机抽样调查，调查的运动项目有：短道速滑、冰壶、单板滑雪、自由式滑雪及其它项目（每位同学仅选一项），根据调查结果绘制了如下统计表：

运动项目	频数/人数	频率
短道速滑	7	0.35
冰壶	2	b
单板滑雪	a	0.25
自由式滑雪	4	0.2
其它	2	0.1

根据以上信息解答下列问题：

(1)、频数分布表中的a = ；

(2)、若将各运动项目的人数所占比例绘制成扇形统计图，则“冰壶”对应扇形的圆心角度数为；

(3)、若在选择“自由式滑雪”的4名学生中，有2名男生，2名女生，现需从这4人中随机抽取2名学生进行项目介绍，请用树状图或列表的方法求所抽取的2名学生恰好是2名男生的概率．

查看试题解析

22. 如图，矩形OABC的边OA、OC分别在y轴和x轴上．反比例函数数y = $\frac{k}{x}$ （x > 0）的图象经过矩形OABC对角线的交点D（4，2），且与边AB，BC分别交干点E，F，直线EF交x轴于点G．

(1)、求点F的坐标；

(2)、求证：四边形AEGC是平行四边形．

查看试题解析
23. 如图，四边形ABCD是⊙O的内接四边形，AB = 6，BC = 8，∠ABC = 90°，弧AD = 弧DC．

(1)、求边CD的长；

(2)、已知△ABE与△ABD关于直线AB对称．
①尺规作图：作△ABE；（保留作图痕迹，不写作法）

②连接DE，求线段DE的长．

查看试题解析
24. 已知抛物线G：y = ax² + bx + c经过点A（-1，a-b+9），且与y轴交于点B，与x轴仅有一个交点．

(1)、求点B的坐标；

(2)、当a + b取最小值时，求抛物线G的解析式；

(3)、若P、C（ $x_{1}$ ，m），D（ $x_{2}$ ，m）（ $x_{1} < x_{2}$ ）为抛物线G上三个不同的点（点P与点B不重合），直线PC，PD与y轴分别交于点E、F，且BF = 5BE，求m的值．

查看试题解析
25. 如图，在等边△ABC中，AB = 6，点D为边BC的中点，点E为边AB上一动点，将线段DE绕点D顺时针旋转60°得到线段DF，射线DF与边AC相交于点G（点G与点A不重合），连接CF，EG．

(1)、求证：△BED∽△CDG；

(2)、点E在边AB上运动的过程中，△AEG的周长是否会发生变化?若不变，求△AEG的周长；若变化，请说明理由；

(3)、设△CDF的面积为 $S_{1}$ .△CGF的面积为 $S_{2}$ ，若 $S_{1}$ = 3 $S_{2}$ ．求△AEG的内切圆半径r．

查看试题解析

x	$\dots$	-3	-2	-1	0	1	$\dots$
y	$\dots$	11	8	5	2	-1	$\dots$