广东省东莞市六校2022年九年级下学期第一次联考(一模)数学试题
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. 计算(﹣2)+(﹣3)的结果是( )A、﹣5 B、﹣1 C、1 D、52. 2022年北京冬季奥运会的吉祥物冰墩墩、雪容融成为冬奥名副其实的顶流,实力演绎“一墩难求”,线上线下曾一度出现缺货,销量最高的一款冰墩墩雪容融手办玩具摆件销量已经超过了6万.6万用科学记数法可表示为( )A、6×105 B、0.6×105 C、6×104 D、0.6×1043. 一个正多边形的每个外角都等于60°,那么它的边数是( )A、6 B、8 C、10 D、124. 若二次根式 在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 从某市5000名初一学生中,随机抽取100名学生,测得他们的身高数据,得到一个样本,则这个样本数据的平均数、中位数、众数、方差四个统计量中,服装厂最感兴趣的是( )A、平均数 B、中位数 C、众数 D、方差7. 不等式组 的整数解有( )A、1个 B、2个 C、3个 D、4个8. 如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
 A、﹣4和﹣3之间 B、﹣5和﹣4之间 C、3和4之间 D、4和5之间9. 如图,将一副直角三角尺按如图位置摆放在同一平面内,使两个直角三角尺的斜边AB∥DF,含30°角的直角三角尺的直角顶点E在含45°角的直角三角尺的斜边AB上,且点F在CB的延长线上,已知∠A=45°,则∠1的度数是( )
A、﹣4和﹣3之间 B、﹣5和﹣4之间 C、3和4之间 D、4和5之间9. 如图,将一副直角三角尺按如图位置摆放在同一平面内,使两个直角三角尺的斜边AB∥DF,含30°角的直角三角尺的直角顶点E在含45°角的直角三角尺的斜边AB上,且点F在CB的延长线上,已知∠A=45°,则∠1的度数是( ) A、30° B、45° C、60° D、75°10. 如图,在四边形 中,AD//BC, .动点P沿路径 从点A出发,以每秒1个单位长度的速度向点D运动.过点P作 ,垂足为H.设点P运动的时间为x(单位:s), 的面积为y,则y关于x的函数图象大致是( )
A、30° B、45° C、60° D、75°10. 如图,在四边形 中,AD//BC, .动点P沿路径 从点A出发,以每秒1个单位长度的速度向点D运动.过点P作 ,垂足为H.设点P运动的时间为x(单位:s), 的面积为y,则y关于x的函数图象大致是( ) A、
A、 B、
B、 C、
C、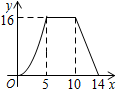 D、
D、
二、填空题
-
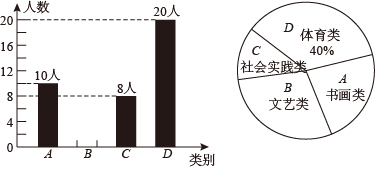
11. 9的算术平方根是 .12. 因式分解: .13. 在△ABC中,∠A,∠B均为锐角,且有 ,则△ABC的形状是 .14. 双减政策背景下,为落实“五育并举”,某学校准备打造学生第二课堂,有四类课程可供选择,分别是“A.书画类、B.文艺类、C.社会实践类、D.体育类” .现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了如下两幅不完整的统计图,若该校七年级共有800名学生,根据上述调查结果估计该校学生选择“社会实践类”的学生共有名.
 15. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,点 、 、 是格点,则图中扇形 中阴影部分的面积是 .
15. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,点 、 、 是格点,则图中扇形 中阴影部分的面积是 .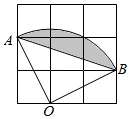 16. 已知 ,则代数式 的值是 .17. 如图,正方形ABCD中, ,O是BC边的中点,点E是正方形内一动点, ,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为 .
16. 已知 ,则代数式 的值是 .17. 如图,正方形ABCD中, ,O是BC边的中点,点E是正方形内一动点, ,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为 .
三、解答题
-
18. 计算:19. 疫情防控,人人有责,而接种疫苗是疫情防控的重要手段,小明和小丽同时去接种疫苗,接种站有北京科兴、北京生物、科兴中维三种疫苗公司生产的疫苗供小明和小丽选择.其中北京科兴、北京生物、科兴中维三种疫苗公司生产的疫苗分别记作A、B、C.(1)、用列表法或画树状图法中的一种方法,求所有可能出现的接种结果;(2)、求小明小丽接种同一家公司生产的疫苗的概率.20. 如图,在 中, 为 的外角.
 (1)、尺规作图:作 的平分线 (保留作图痕迹可加黑,不写作法);(2)、若 ,在(1)的条件下,求证: .21. 某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.(1)、求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?(2)、学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.22. 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′.
(1)、尺规作图:作 的平分线 (保留作图痕迹可加黑,不写作法);(2)、若 ,在(1)的条件下,求证: .21. 某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.(1)、求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?(2)、学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.22. 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′. (1)、证明△A′AD′≌△CC′B;(2)、若∠ACB=30°,试问当点C′在线段AC上的什么位置时,四边形ABC′D′是菱形,并请说明理由.23. Rt ABC在直角坐标系内的位置如图所示,反比例函数y= (k≠0)在第一象限内的图象与BC边交于点D(4,1),与AB边交于点E(2,n).
(1)、证明△A′AD′≌△CC′B;(2)、若∠ACB=30°,试问当点C′在线段AC上的什么位置时,四边形ABC′D′是菱形,并请说明理由.23. Rt ABC在直角坐标系内的位置如图所示,反比例函数y= (k≠0)在第一象限内的图象与BC边交于点D(4,1),与AB边交于点E(2,n). (1)、求反比例函数的解析式和n值;(2)、当 时,求直线AB的解析式.24. 如图,已知点O是△ABC的外接圆的圆心,AB=AC,点D是弧AB上一点,连接并延长BD交过点A且平行于BC的射线于点E.
(1)、求反比例函数的解析式和n值;(2)、当 时,求直线AB的解析式.24. 如图,已知点O是△ABC的外接圆的圆心,AB=AC,点D是弧AB上一点,连接并延长BD交过点A且平行于BC的射线于点E. (1)、求证:DA平分∠CDE;(2)、判断直线AE与⊙O的位置关系,并证明;(3)、若DE=3,BD=6,AD=5,求AC的长.25. 如图,抛物线y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,且OB=OC.
(1)、求证:DA平分∠CDE;(2)、判断直线AE与⊙O的位置关系,并证明;(3)、若DE=3,BD=6,AD=5,求AC的长.25. 如图,抛物线y=ax2-2ax-3a(a>0)与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,且OB=OC.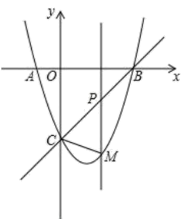 (1)、求抛物线的解析式;(2)、如图,若点P是线段BC(不与B,C重合)上一动点,过点P作x轴的垂线交抛物线于M点,连接CM,当△PCM和△ABC相似时,求此时点P的坐标;(3)、若点P是直线BC(不与B,C重合)上一动点,过点P作x轴的垂线交抛物线于M点,连接CM,将△PCM沿CM对折,如果点P的对应点N恰好落在y轴上,求此时点P的坐标;
(1)、求抛物线的解析式;(2)、如图,若点P是线段BC(不与B,C重合)上一动点,过点P作x轴的垂线交抛物线于M点,连接CM,当△PCM和△ABC相似时,求此时点P的坐标;(3)、若点P是直线BC(不与B,C重合)上一动点,过点P作x轴的垂线交抛物线于M点,连接CM,将△PCM沿CM对折,如果点P的对应点N恰好落在y轴上,求此时点P的坐标;