浙江省宁波市鄞州区九校联考2022届九年级下学期月考数学试卷(一模)
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. 下列各数中,绝对值最小的数是( )A、0 B、-4 C、3 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 北京2022年冬奥会开幕式完美上演,中国以自己的方式,为世界呈现了一场浪漫十足的冰雪盛宴.据官方数据统计,中国大陆地区观看人数约3.16亿人.3.16亿用科学记数法表示为( )A、 B、 C、 D、4. 如图所示的几何体的俯视图( )
 A、
A、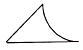 B、
B、 C、
C、 D、
D、 5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数( )
185
180
185
180
方差
3.6
4.6
5.4
6.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁6. 能说明命题“对于任意实数 , ”是假命题的反例为( )A、 B、 C、 D、7. 用一把剪刀将一张直角三角形纸片剪成两个三角形,则这两个三角形一定不会是( )A、两个相似三角形 B、两个等腰三角形 C、两个锐角三角形 D、两个周长相等的三角形8. 某商店有方形、圆形两种巧克力,小明如果购买3块方形和5块圆形巧克力,他带的钱会差8元,如果购买5块方形和3块圆形巧克力,他带的钱会剩下8元.若他只购买8块方形巧克力,则他会剩下( )元A、8 B、16 C、24 D、329. 二次函数 的图象如图所示.下列结论:① ;② ;③ 为任意实数,则 ;④ ;⑤若 且 ,则 .其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个10. 在矩形 内,将两张边长分别为 和 的正方形纸片按图①,图②两种方式放置(图①,图②中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,若图①中阴影部分面积为 ,图②中阴影部分的面积和为 .则 的值表示正确的是( )
A、1个 B、2个 C、3个 D、4个10. 在矩形 内,将两张边长分别为 和 的正方形纸片按图①,图②两种方式放置(图①,图②中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,若图①中阴影部分面积为 ,图②中阴影部分的面积和为 .则 的值表示正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算:= .
12. 不透明袋子中有4个红球和5个绿球,这些球除颜色外无其他差别,从袋子中随机取出1个球,恰好是红球的概率为.13. 一个圆锥的底面半径为 ,侧面展开图的圆心角为 ,则这个圆锥体的侧面积为 .14. 如图,在矩形 中, , , 是对角线 上的动点,以点 为圆心, 长为半径作 .当 与矩形 的边相切时, 的长为. 15. 如图,点A、B都在双曲线 上,直线AB与x轴的负半轴交于点C,且点A,B的纵坐标分别是3和1,△AOC的面积是4.5,则k的值为.
15. 如图,点A、B都在双曲线 上,直线AB与x轴的负半轴交于点C,且点A,B的纵坐标分别是3和1,△AOC的面积是4.5,则k的值为. 16. 如图,在等边 中,将 绕顶点 顺时针旋转,旋转角为 ,得到 .设 的中点为 , 的中点为 , ,连接 .
16. 如图,在等边 中,将 绕顶点 顺时针旋转,旋转角为 ,得到 .设 的中点为 , 的中点为 , ,连接 . (1)、当 时, 的长度为;(2)、设 ,在整个旋转过程中, 的取值范围是.
(1)、当 时, 的长度为;(2)、设 ,在整个旋转过程中, 的取值范围是.三、解答题
-
17.(1)、计算:6sin60°+ ;(2)、解不等式组: .18. 图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.
 (1)、在图①、图②中,以格点为顶点,线段AB为一边,分别画一个平行四边形和菱形,并直接写出它们的面积.(要求两个四边形不全等)(2)、在图③中,以点A为顶点,另外三个顶点也在格点上,画一个面积最大的正方形,并直接写出它的面积.19. 图1是某小型汽车的侧面示意图,其中矩形 表示该车的后备箱,在打开后备箱的过程中,箱盖 可以绕点 逆时针方向旋转,当旋转角为 时,箱盖 落在 的位置(如图2所示)已知 厘米, 厘米, 厘米.
(1)、在图①、图②中,以格点为顶点,线段AB为一边,分别画一个平行四边形和菱形,并直接写出它们的面积.(要求两个四边形不全等)(2)、在图③中,以点A为顶点,另外三个顶点也在格点上,画一个面积最大的正方形,并直接写出它的面积.19. 图1是某小型汽车的侧面示意图,其中矩形 表示该车的后备箱,在打开后备箱的过程中,箱盖 可以绕点 逆时针方向旋转,当旋转角为 时,箱盖 落在 的位置(如图2所示)已知 厘米, 厘米, 厘米. (1)、求点 到 的距离;(结果保留根号)(2)、求 、 两点的距离.(结果保留根号)20. 为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
(1)、求点 到 的距离;(结果保留根号)(2)、求 、 两点的距离.(结果保留根号)20. 为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
10
10
15
40
25
20
请根据调查的信息分析:
(1)、活动启动之初学生“一周诗词诵背数量”的中位数为;(2)、估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;(3)、选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.21. 如图,已知抛物线 经过 、 两点.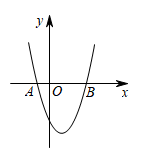 (1)、求抛物线的解析式和顶点坐标;(2)、当 时,求 的取值范围;(3)、点P为抛物线上一点,若 ,求出此时点P的坐标.22. 甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量 (个)与加工时间 (分)之间的函数关系,观察图象解决下列问题:
(1)、求抛物线的解析式和顶点坐标;(2)、当 时,求 的取值范围;(3)、点P为抛物线上一点,若 ,求出此时点P的坐标.22. 甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量 (个)与加工时间 (分)之间的函数关系,观察图象解决下列问题: (1)、点 的坐标是 , 点表示的实际意义是;(2)、在加工的过程中,多少分钟时甲比乙多加工100个零件?(3)、为了使乙能与甲同时完成任务,现让丙帮乙一起加工,直到完成任务.已知丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第几分钟时开始帮助乙?并在图中画出丙帮助乙后 与 之间的函数关系的图象.23. 如图
(1)、点 的坐标是 , 点表示的实际意义是;(2)、在加工的过程中,多少分钟时甲比乙多加工100个零件?(3)、为了使乙能与甲同时完成任务,现让丙帮乙一起加工,直到完成任务.已知丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第几分钟时开始帮助乙?并在图中画出丙帮助乙后 与 之间的函数关系的图象.23. 如图 (1)、证明推断:如图(1),在正方形ABCD中,点E,Q分别在边BC,AB上,DQ⊥AE于点O,点G,F分别在边CD,AB上,GF⊥AE.
(1)、证明推断:如图(1),在正方形ABCD中,点E,Q分别在边BC,AB上,DQ⊥AE于点O,点G,F分别在边CD,AB上,GF⊥AE.①求证:DQ=AE;
②推断: 的值为▲ ;
(2)、类比探究:如图(2),在矩形ABCD中, =k(k为常数).将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形FEPG,EP交CD于点H,连接AE交GF于点O.试探究GF与AE之间的数量关系,并说明理由;(3)、拓展应用:在(2)的条件下,连接CP,当k= 时,若tan∠CGP= ,GF=2 ,求CP的长.24. 如图,AB为⊙O的直径,弦CD交AB于点E,且DE=OE. (1)、求证:∠BAC=3∠ACD;(2)、点F在弧BD上,且∠CDF= ∠AEC,连接CF交AB于点G,求证:CF=CD;(3)、①在(2)的条件下,若OG=4,设OE=x,FG=y,求y关于x的函数关系式;
(1)、求证:∠BAC=3∠ACD;(2)、点F在弧BD上,且∠CDF= ∠AEC,连接CF交AB于点G,求证:CF=CD;(3)、①在(2)的条件下,若OG=4,设OE=x,FG=y,求y关于x的函数关系式;②求出使得y有意义的x的最小整数值,并求出此时⊙O的半径.