浙江省宁波市海曙区2022届九年级下学期期中数学试题(一模)
试卷更新日期:2022-05-17 类型:中考模拟
一、单选题
-
1. 要使 有意义, 的取值范围是( )A、 B、 C、 D、2. 下列方程中,属于一元二次方程的是( )A、 B、 C、 D、3. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、5. 八年级一班的平均年龄是14.2岁,方差是40,过一年后该班学生到九年级时,下列说法正确的是( )A、平均年龄不变 B、年龄的众数不变 C、年龄的方差不变 D、年龄的中位数不变6. 一个多边形的内角和是外角和的2倍,这个多边形的边数为( )A、5 B、6 C、7 D、87. 小明进行了5次一分钟跳绳训练,计算出这5次跳绳的平均成绩为176个,方差为 ,随后小明又进行了第6次跳绳,成绩恰好是176个,并计算出了这6次跳绳的方差为 ,则下列说法正确的是( )A、 B、 C、 D、无法确定 与 的大小8. 利用反证法证明命题“四边形中至少有一个角是钝角或直角”时,应假设( )A、四边形中至多有一个内角是钝角或直角 B、四边形的每一个内角都是钝角或直 C、四边形中所有内角都是锐角 D、四边形中所有内角都是直角9. 关于x的一元二次方程 有两个实数根,则实数m的取值范围是( )A、m≥0 B、m>0 C、m≥0且m≠1 D、m>0且m≠110. 如图,在平行四边形 中, , 于点 , 为 的中点,连结 , ,下列结论:① ,② ;③ ;④ ,其中正确结论的个数共有( )
4. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、5. 八年级一班的平均年龄是14.2岁,方差是40,过一年后该班学生到九年级时,下列说法正确的是( )A、平均年龄不变 B、年龄的众数不变 C、年龄的方差不变 D、年龄的中位数不变6. 一个多边形的内角和是外角和的2倍,这个多边形的边数为( )A、5 B、6 C、7 D、87. 小明进行了5次一分钟跳绳训练,计算出这5次跳绳的平均成绩为176个,方差为 ,随后小明又进行了第6次跳绳,成绩恰好是176个,并计算出了这6次跳绳的方差为 ,则下列说法正确的是( )A、 B、 C、 D、无法确定 与 的大小8. 利用反证法证明命题“四边形中至少有一个角是钝角或直角”时,应假设( )A、四边形中至多有一个内角是钝角或直角 B、四边形的每一个内角都是钝角或直 C、四边形中所有内角都是锐角 D、四边形中所有内角都是直角9. 关于x的一元二次方程 有两个实数根,则实数m的取值范围是( )A、m≥0 B、m>0 C、m≥0且m≠1 D、m>0且m≠110. 如图,在平行四边形 中, , 于点 , 为 的中点,连结 , ,下列结论:① ,② ;③ ;④ ,其中正确结论的个数共有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
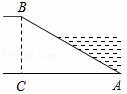
11. 计算: .12. 若 是方程 一个根,则代数式 的值为.13. 如图,河坝横断面迎水坡AB的坡比是1: (坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3m,则坡面AB的长度是 .
 14. 一组从小到大排列的数据为:1,5, ,y, ,12的平均数与中位数都是7,则这组数的众数是.15. 受疫情影响,某快递公司的投递业务锐减,已知今年1月份与3月份完成的快递总件数分别为25万件和16万件,若假设快递量平均每月降低率为 ,则可列出方程.16. 如图,在 中, , 、 分别是 、 的中点,延长 至点 ,使 ,连接 、 ,若 ,则 的长为.
14. 一组从小到大排列的数据为:1,5, ,y, ,12的平均数与中位数都是7,则这组数的众数是.15. 受疫情影响,某快递公司的投递业务锐减,已知今年1月份与3月份完成的快递总件数分别为25万件和16万件,若假设快递量平均每月降低率为 ,则可列出方程.16. 如图,在 中, , 、 分别是 、 的中点,延长 至点 ,使 ,连接 、 ,若 ,则 的长为.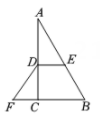 17. 如图,一副三角板如图1放置, ,顶点 重合,将 绕其顶点 旋转,如图2,在旋转过程中,当 ,连接 , ,此时四边形 的面积是.
17. 如图,一副三角板如图1放置, ,顶点 重合,将 绕其顶点 旋转,如图2,在旋转过程中,当 ,连接 , ,此时四边形 的面积是. 18. 在平面直角坐标系中, , , ,点 在直线 上,若以 , , , 四点为顶点的四边形是平行四边形,则点D的坐标为.
18. 在平面直角坐标系中, , , ,点 在直线 上,若以 , , , 四点为顶点的四边形是平行四边形,则点D的坐标为.三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、 ;(2)、 .21. 某中学举办“垃圾分类知识答题竞赛”,七年级和八年级根据初赛成绩各选出5名选手参加学校决赛,成绩如图所示.

平均分
中位数
众数
方差
七年级
a
85
b
S2
八年级
85
c
100
160
(1)、直接写出a、b、c的值;(2)、结合两个年级成绩的平均数和中位数进行分析,哪个年级的决赛成绩好;(3)、计算七年级决赛成绩的方差S2 , 并判断哪个年级的选手成绩较为稳定.22. 如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF, (1)、求证:AE=CF;(2)、求证:四边形AECF是平行四边形.23. 某超市销售一种衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,加盈利,该超市准备适当降价,经过一段时间测算,发现每件衬衫每降低1元,平均每天可多售出2件.(1)、若每件衬衫降价4元时,平均每天可售出多少件衬衫?此时每天销售获利多少元?(2)、在每件盈利不少于25元的前提下,要使该衬衫每天销售获利为1200元,同每件衬衫应降价多少元?(3)、该衬衫每天的销售获利能达到1300元吗?如果能,请写出降价方案,如果不能,请说明理由.24. 类比于等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)、求证:AE=CF;(2)、求证:四边形AECF是平行四边形.23. 某超市销售一种衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,加盈利,该超市准备适当降价,经过一段时间测算,发现每件衬衫每降低1元,平均每天可多售出2件.(1)、若每件衬衫降价4元时,平均每天可售出多少件衬衫?此时每天销售获利多少元?(2)、在每件盈利不少于25元的前提下,要使该衬衫每天销售获利为1200元,同每件衬衫应降价多少元?(3)、该衬衫每天的销售获利能达到1300元吗?如果能,请写出降价方案,如果不能,请说明理由.24. 类比于等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”. (1)、如图1,四边形 的顶点A,B,C在网格格点上,请你在 的网格中分别画出3个不同形状的等邻边四边形 ,要求顶点D在网格格点上,(2)、如图2,在平行四边形 中,E是 上一点, 是 上一点, , ,请说明四边形ABEF是“等邻边四边形”.(3)、如图3,在平行四边形 中, , 平分 ,交 于点 , , , 是线段 上一点,当四边形ABEF是“等邻边四边形”时,请直接写出DF的长度.
(1)、如图1,四边形 的顶点A,B,C在网格格点上,请你在 的网格中分别画出3个不同形状的等邻边四边形 ,要求顶点D在网格格点上,(2)、如图2,在平行四边形 中,E是 上一点, 是 上一点, , ,请说明四边形ABEF是“等邻边四边形”.(3)、如图3,在平行四边形 中, , 平分 ,交 于点 , , , 是线段 上一点,当四边形ABEF是“等邻边四边形”时,请直接写出DF的长度.