浙江省杭州市萧山区2021-2022学年七年级下学期期中数学试卷

试卷更新日期：2022-05-17 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，∠1和∠2不是同位角的是（　　）

A、 B、 C、 D、

查看试题解析
2. 一个新型冠状病毒的直径约是0.00000011米，将0.00000011用科学记数法表示为（）

A、 $1.1 \times 10^{- 7}$ B、 $1.1 \times 10^{- 8}$ C、 $0.11 \times 10^{- 7}$ D、 $11 \times 10^{- 8}$

查看试题解析
3. 如图，若 $A B / / C D$ ，则下列结论正确的是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 2 = ∠ 4$ C、 $∠ A = ∠ C$ D、 $∠ 2 = ∠ 3$

查看试题解析
4. 下列计算正确的是（）

A、 ${(x^{3})}^{2} = x^{5}$ B、 $x^{4} - x^{2} = x^{2}$ C、 $x^{8} \div x^{4} = x^{2}$ D、 $x^{2} \cdot x^{3} = x^{5}$

查看试题解析
5. 下列等式从左到右变形，属于因式分解的是（）

A、 $x + 2 y = (x + y) + y$ B、 $p (q + h) = p q + p h$ C、 $5 x^{2} y - 10 x y^{2} = 5 x y (x - 2 y)$ D、 $4 a^{2} - 4 a + 1 = 4 a (a - 1) + 1$

查看试题解析
6. 一行人去住店，如果每一间客房住7人，那么有7人无房可住；如果每一间客房住9人，那么就空出一间房.设该店有空客房x间，这一行人共有y人，下列方程组中正确的是（）

A、 ${\begin{matrix} 7 x + 7 = y \\ 9 (x + 1) = y \end{matrix}$ B、 ${\begin{array}{l} 7 x + 7 = y \\ 9 (x - 1) = y \end{array}$ C、 ${\begin{array}{l} 7 x - 7 = y \\ 9 (x - 1) = y \end{array}$ D、 ${\begin{matrix} 7 x - 7 = y \\ 9 (x + 1) = y \end{matrix}$

查看试题解析
7. 若 $x^{m} = 5$ ， $x^{n} = \frac{1}{4}$ ，则 $x^{2 m - n} =$ （）

A、 $\frac{5}{2}$ B、 $40$ C、 $\frac{25}{4}$ D、 $100$

查看试题解析
8. 如图，在 $△ A B C$ 中， $∠ A = 30 °$ ，点 $D$ 是 $A B$ 延长线上一点，过点 $D$ 作 $E F ∥ B C$ ．若 $∠ A D E = 70 °$ ，则 $∠ C$ 的度数为（）

A、20° B、30° C、40° D、50°

查看试题解析
9. 若x是不为0的有理数，已知M＝（x²+2x+1）（x²﹣2x+1），N＝（x²+x+1）（x²﹣x+1），则M与N的大小是（）

A、M＞N B、M＜N C、M＝N D、无法确定

查看试题解析
10. 已知关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - 5 y = 3 a \end{array}$ ，给出下列结论：① ${\begin{array}{l} x = 5 \\ y = - 1 \end{array}$ 是方程组的解；②无论 $a$ 取何值， $x$ ， $y$ 的值都不可能互为相反数；③当 $a = 1$ 时，方程组的解也是方程 $x + y = 4 - a$ 的解；④ $x$ ， $y$ 的都为自然数的解有4对.其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 现有1元的人民币 $x$ 张，5元的人民币 $y$ 张，共120元，这个关系用方程可以表示为.

查看试题解析
12. 分解因式： $a^{2} - a b$ = ．

查看试题解析
13. 已知m+n=mn，则 $(1 - m) (1 - n) =$ .

查看试题解析
14. 如图，将△ABC沿BC方向平移到△DEF，若A、D间的距离为1，CE＝2，则BF＝．

查看试题解析
15. 如图，将三角形ABC沿着DE折叠，使点A落在BC上的点F处，且DE∥BC，若∠B=70°，则∠BDF= .

查看试题解析
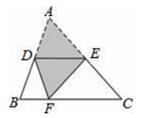16. 关于 x，y 的方程组 ${\begin{matrix} a^{2} x + b^{2} y = 1 + 2 a b \\ b^{2} x + a^{2} y = 1 - 2 a b \end{matrix}$ 的解为 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ ，则①a²+ b²②关于 x，y 的方程组 ${\begin{matrix} a^{2} (x - 1) + b^{2} (y - 1) = \frac{1}{2} + a b \\ b^{2} (x - 1) + a^{2} (y - 1) = \frac{1}{2} - a b \end{matrix}$ 的解为.

查看试题解析

三、解答题

17. 计算或化简：

(1)、 $2^{- 3}$ + ${(\sqrt{5} - 3)}^{0}$

(2)、 $(4 a^{3} - 6 a^{2})$ $\div (2 a^{2})$

查看试题解析
18. 解下列方程组：

(1)、 ${\begin{matrix} x = y + 5 \\ 2 x - y = 8 \end{matrix}$

(2)、 ${\begin{array}{l} 2 x + 3 y = 3 \\ 3 x - 2 y = 11 \end{array}$

查看试题解析
19. 已知 $x^{2} - x - 3 = 0$ ，求代数式 ${(x - 1)}^{2} + (x - 1) (2 x + 1)$ 的值．

查看试题解析
20. 疫情期间为保护学生和教师的健康，某学校储备“抗疫物资”，用19000元购进甲、乙两种医用口罩共计900盒，甲、乙两种口罩的售价分别是20元/盒，25元/盒.

(1)、求甲、乙两种口罩各购进了多少盒？

(2)、现已知甲、乙两种口罩的数量分别是20个/盒，25个/盒，按照市教育局要求，学校必须储备足够使用10天的口罩，该校师生共计900人，每人每天2个口罩，问购买的口罩数量是否能满足市教育局的要求？

查看试题解析
21. 如图，已知 $A 、 B 、 C$ 三点在同一直线上， $∠ 1 = ∠ 2 ， ∠ D = ∠ 3$ .

(1)、说明 $B D / / C E$ 的理由.

(2)、若 $∠ C = 68 ° ， ∠ D A C = 52 °$ ，求 $∠ D B E$ 的度数.

查看试题解析
22. 在学了乘法公式“ ${(a \pm b)}^{2} = a^{2} \pm 2 a b + b^{2}$ ”的应用后，王老师提出问题：求代数式 $x^{2} + 4 x + 5$ 的最小值.要求同学们运用所学知识进行解答.
同学们经过探索、交流和讨论，最后总结出如下解答方法：

解： $x^{2} + 4 x + 5 = x^{2} + 4 x + 2^{2} - 2^{2} + 5 = {(x + 2)}^{2} + 1$ ，

∵ ${(x + 2)}^{2} \geq 0$ ，∴ ${(x + 2)}^{2} + 1 \geq 1$ .

当 ${(x + 2)}^{2} = 0$ 时， ${(x + 2)}^{2} + 1$ 的值最小，最小值是1.

∴ $x^{2} + 4 x + 5$ 的最小值是1.

请你根据上述方法，解答下列各题：

(1)、直接写出 ${(x - 1)}^{2} + 3$ 的最小值为.

(2)、求代数式 $x^{2} + 10 x + 32$ 的最小值.

(3)、若 $7 x - x^{2} + y - 11 = 0$ ，求 $x + y$ 的最小值.

查看试题解析
23. 已知AB∥CD，点E在AB上，点G在CD上，点F在直线AB、CD之间，分别连接EF、FG，∠BEF+∠DGF=2∠EFG

(1)、如图1，求∠EFG的度数；

(2)、如图2，若∠BEF的角平分线与FG的延长线交于点M，求证：∠AEF－2∠FME=60°；

(3)、如图3，已知点P在FG的延长线上，点K在CD上，点N在∠PGC内，分别连接NG，NK.若NK∥EF，∠PGN=2∠NGC，请直接写出 $∠ A E F - \frac{3}{2} ∠ G N K$ 的值

查看试题解析