浙江省绍兴市诸暨市暨阳教育共同体2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-05-17 类型：期中考试

进入出卷网下载

一、单选题

1. 下列式子是最简二次根式的是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{0.5}$ C、 $\sqrt{5}$ D、 $\sqrt{27}$

查看试题解析
2. 下列方程中，属于一元二次方程的是（）

A、 $2 x + y = 3$ B、 $x^{2} + 3 x = 0$ C、 $\frac{1}{x^{2}} - x = 0$ D、 $2 x + 1 = 0$

查看试题解析
3. 在某校“我的中国梦”演讲比赛中，有9名学生参加决赛，他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名，不仅要了解自己的成绩，还要了解这9名学生成绩的( )

A、众数 B、方差 C、平均数 D、中位数

查看试题解析
4. 一个多边形的内角和与外角和相等，则这个多边形是（）

A、四边形 B、五边形 C、六边形 D、八边形

查看试题解析
5. 某平行四边形的一条边长为12cm，则它的两条对角线长可以为（）

A、6cm，12cm B、18cm，20cm C、34cm，10cm D、10cm，14cm

查看试题解析
6. 某超市一月份的营业额为300万元，第一季度的营业额共为1500万元，如果平均每月增长率为 $x$ ，则由题意可列方程为（）

A、 $300 {(1 + x)}^{2} = 1500$ B、 $300 + 300 \times 2 x = 1500$ C、 $300 + 300 \times 3 x = 1500$ D、 $300 [1 + (1 + x) + {(1 + x)}^{2}] = 1500$

查看试题解析
7. 用配方法解一元二次方程 $x^{2} - 4 x + 3 = 0$ 时可配方得（）

A、 ${(x - 2)}^{2} = 7$ B、 ${(x - 2)}^{2} = 1$ C、 ${(x + 2)}^{2} = 1$ D、 ${(x + 2)}^{2} = 2$

查看试题解析
8. 如果1≤a≤ $\sqrt{2}$ ，则 $\sqrt{a^{2} - 2 a + 1}$ +|a-2|的值是（　　）

A、6+a B、﹣6﹣a C、﹣a D、1

查看试题解析
9. 已知关于 $x$ 的方程 ${kx}^{2} + (1 - k) x - 1 = 0$ ，下列说法正确的是（）

A、当 $k = 0$ 时，方程无解 B、当 $k = 1$ 时，方程有一个实数解 C、当 $k = - 1$ 时，方程有两个相等的实数解 D、当 $k \neq 0$ 时，方程总有两个不相等的实数解

查看试题解析
10. 如图所示，点E为 $▱ A B C D$ 内一点，连结 $E A ， E B ， E C ， E D ， A C$ ，已知 $△ B C E$ 的面积为2， $△ C E D$ 的面积为10，则阴影部分 $△ A C E$ 的面积为（）

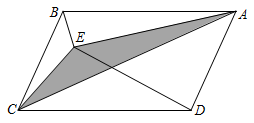A、5 B、6 C、7 D、8

查看试题解析

二、填空题

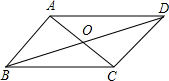
11. 若二次根式 $\sqrt{a + 1}$ 有意义，则 $a$ 的取值范围是.

查看试题解析
12. 在平行四边形 $A B C D$ 中， $∠ A + ∠ C = 220^{\circ}$ ，则 $∠ B =$ 度.

查看试题解析
13. 为了考察甲、乙两种小麦的长势，分别从中抽出20株测得其高度，并求得它们的方差分别为 $s_{甲}^{2} = 3.6$ ， $s_{乙}^{2} = 15.8$ ，则种小麦的长势比较整齐.

查看试题解析
14. 已知数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的平均数是5，方差是2.则数据 $2 x_{1} - 3 ； 2 x_{2} - 3 ； 2 x_{3} - 3$ 的平均数是，方差是.

查看试题解析
15. 若关于x的一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则a的值是

查看试题解析
16. 如图所示，在平行四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，已知 $△ B O C$ 与 $△ A O B$ 的周长之差为3，平行四边形 $A B C D$ 的周长为30，则 $B C$ 的长度为.

查看试题解析
17. 对于实数 $a ， b$ ，定义运算“◎”如下： $a$ ◎ $b$ $= {(a + b)}^{2} - {(a - b)}^{2}$ .若 $(m + 2)$ ◎ $(m - 3)$ $= 24$ ，则 $m =$ .

查看试题解析
18. 如图，是一个长为30m，宽为20m的矩形花园，现要在花园中修建等宽的小道，剩余的地方种植花草.如图所示，要使种植花草的面积为468m² ，那么小道进出口的宽度应为 m.

查看试题解析
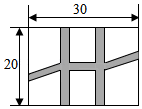19. 已知等腰三角形的每条边长都是一元二次方程 $x^{2} - 7 x + 10 = 0$ 的根，则这个三角形的周长为；

查看试题解析
20. 如图所示，在平行四边形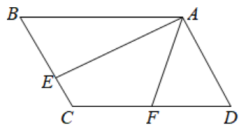 $A B C D$ 中，点E在线段 $B C$ 上且 $B E = 2 C E$ ，点F是 $C D$ 边的中点，若 $A E = 4 \sqrt{2}$ ， $A F = 4$ ，且 $∠ E A F = 45 °$ ，则 $A B$ 的长是.

查看试题解析

三、解答题

21. 化简：

(1)、 $2 \sqrt{20} - \sqrt{5} + 2 \sqrt{\frac{1}{5}}$

(2)、 $(\sqrt{48} - \sqrt{27}) \div \sqrt{3}$

查看试题解析
22. 解一元二次方程：

(1)、 $2 x^{2} + 5 x - 3 = 0$

(2)、 ${(x - 3)}^{2} = 4 x - 12$

查看试题解析
23. 2020年是特殊的一年，这一年我们经历了新型冠状病毒肺炎疫情，举国上下众志成城，共同抗疫.口罩成为人们防护防疫的必备武器.西安某药店有3000枚口罩准备出售，从中随机抽取了一部分口罩，根据它们的价格（单位：元），绘制出如图的统计图.请根据相关信息，解答下列问题：

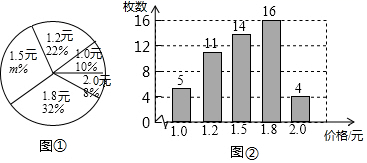(1)、图①中 $m$ 的值为；

(2)、统计的这组数据的中位数为；众数为；

(3)、根据样本数据，估计这3000枚口罩中，价格为1.8元的口罩有多少枚？

查看试题解析
24. 如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使 $B F = B E$ ，连接EC并延长，使 $C G = C E$ ，连接FG，H为FG的中点，连接DH

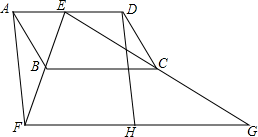(1)、求证：四边形AFHD为平行四边形；

(2)、若 $C B = C E$ ， $∠ E B C = 75 °$ ， $∠ D C E = 10 °$ ，求 $∠ D A B$ 的度数.

查看试题解析
25. 某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，增加利润，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件.

(1)、每件童装降价多少元时，平均每天赢利1200元.

(2)、要想平均每天赢利2000元，可能吗？请说明理由

查看试题解析
26. 如图，在四边形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21.动点P从点D出发，沿线段DA的方向以每秒2个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点P运动到点A时，点Q随之停止运动.设运动的时间为t（秒）.

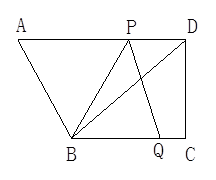(1)、当t=2时，求△BPQ的面积；

(2)、若四边形ABQP为平行四边形，求运动时间t.

(3)、当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？

查看试题解析