浙江省嘉兴市2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-05-17 类型：期中考试

进入出卷网下载

一、单选题

1. 以下关于新型冠状病毒的防范宣传图标中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 要使式子 $\frac{\sqrt{a + 2}}{a}$ 有意义，则a的取值范围是（）

A、a≠0 B、a＞﹣2且 a≠0 C、a＞﹣2或 a≠0 D、a≥﹣2且 a≠0

查看试题解析
3. 下列计算，正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{(- 2) \times (- 2)} = 2$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$

查看试题解析
4. 用配方法解方程 $x^{2} - 2 x - 5 = 0$ 时，原方程应变形为（）

A、 ${(x + 1)}^{2} = 6$ B、 ${(x - 1)}^{2} = 6$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
5. 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：

尺码

$39$

$40$

$41$

$42$

$43$

平均每天销售数量（件）

$10$

$12$

$20$

$12$

$12$

该店主决定本周进货时，增加了一些 $41$ 码的衬衫，影响该店主决策的统计量是（）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
6. 如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，若∠1=32°，∠3=60°，则∠2等于（）

A、92° B、88° C、98° D、无法确定

查看试题解析
7. 某校规定学生的学期数学成绩满分为100分，其中研究性学习成绩占40%，期末卷面成绩占60%，小明的两项成绩（百分制）依次是80分，90分，则小明这学期的数学成绩是（）

A、80分 B、82分 C、84分 D、86分

查看试题解析
8. 实数 $a$ ， $b$ 在数轴上对应的点的位置如图所示，化简 $| a | + \sqrt{{(a - b)}^{2}}$ 的结果是（）

A、 $- 2 a + b$ B、 $2 a - b$ C、 $- b$ D、 $b$

查看试题解析
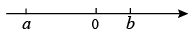9. 如图，一块长方形绿地的长为100m，宽为50m，在绿地中开辟两条道路后剩余绿地面积为4704m²。则根据题意可列出方程（）

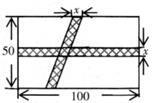A、5000-150x=4704 B、5000-150x+x²=4704 C、5000-150x-x²=4704 D、5000-150x+ $\frac{1}{2}$ x²=4704

查看试题解析
10. 如图，在平行四边形ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则以下结论：① ∠DCF= $\frac{1}{2}$ ∠BCD；②EF＝CF；③S_△ABC＝2S_△CEF；④∠DFE＝3∠AEF，一定成立的是（）

A、①② B、②③④ C、①②③ D、①②④

查看试题解析

二、填空题

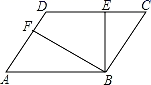
11. 一个正n边形的内角和是它外角和的3倍，则n＝.

查看试题解析
12. 写出一个解为x=2或x=-3的一元二次方程.

查看试题解析
13. 当 $x = - 1$ 时，二次根式 $\sqrt{3 - x}$ 的值是.

查看试题解析
14. 已知a，b，c，d，e五个数的平均数是3，那么a+10，b+6，c+12，d+14，e+8五个数的平均数是.

查看试题解析
15. 计算： $\sqrt{{(1 - \sqrt{2})}^{2}}$ ＝

查看试题解析
16. 若实数a、b满足等式 $| a - 3 | + \sqrt{b - 6} = 0$ ，且a、b恰好是等腰三角形 $△ A B C$ 的边长，则这个等腰三角形的周长是.

查看试题解析
17. 若方程 $（ m + 2 ） x^{m^{2} - 2} + （ m - 1 ） x - 2 = 0$ 是关于x的一元二次方程，则m的值为.

查看试题解析
18. 关于x的方程 $a x^{2} - 5 x - 1 = 0$ 有两个实数根，则a的取值范围是.

查看试题解析
19. 若一组数据1，2， $x$ ，3，4的平均数是3，则这组数据的方差是.

查看试题解析
20. 如图，在平行四边形ABCD中，BE⊥CD，BF⊥AD，垂足分别为E，F，CE＝2，DF＝1，∠EBF＝60°，则平行四边形ABCD的周长为.

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt{8} - \sqrt{2}$ ；

(2)、 $(1 + \sqrt{2}) (1 - \sqrt{2}) - \sqrt{50}$

查看试题解析
22. 解方程：

(1)、x²–4x + 3＝0；

(2)、x（x – 1）＝2（x – 1）

查看试题解析
23. 如图，在平面直角坐标系中，已知△ABC的三个顶点都在格点上.

(1)、请按下列要求画图：
①将△ABC先向右平移5个单位，再向上平移1个单位，得到△A₁B₁C₁ ，画出△A₁B₁C₁；

②△A₂B₂C₂与△ABC关于原点O成中心对称，画出△A₂B₂C₂；

(2)、若（1）所得的△A₁B₁C₁与△A₂B₂C₂ ，关于点P成中心对称，直接写出对称中心P点的坐标.

查看试题解析
24. 为弘扬中华传统文化，感受中华诗词的独特魅力，某校团委举办首届“校园诗词大会”，初赛共10道题，每题10分，小明从初赛名单中随机抽取部分同学的成绩，绘制出如下的统计图1和图2，请根据相关信息，解答下列问题：

(1)、图1中a的值为▲ ，补全条形统计图；

(2)、求被抽取的初赛成绩的平均数，众数和中位数；

(3)、如果初赛成绩在90分或90分以上的同学进入复赛，请估计参加初赛的160名同学中有多少名可以参加复赛.

查看试题解析
25. 如图，在平行四边形ABCD中，AE、CF分别平分∠BAD和∠DCB，交对角线BD于点E、F.

(1)、若∠BCF=55°，求∠ABC的度数；

(2)、求证：BF=DE.

查看试题解析
26. 山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：

(1)、每千克核桃应降价多少元？

(2)、在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？

查看试题解析

尺码	$39$	$40$	$41$	$42$	$43$
平均每天销售数量（件）	$10$	$12$	$20$	$12$	$12$