浙江省宁波市鄞州区2021-2022学年七年级下学期期中联考数学试卷

试卷更新日期：2022-05-17 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列运算正确的是 $($ $)$

A、 $a + a = a^{2}$ B、 ${(a^{3})}^{2} = a^{6}$ C、 $a^{2} \cdot a = 2 a^{2}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
2. 国产手机芯片麒麟980是全球首个7纳米制程芯片，已知1纳米 $= 0.000000001$ 米，则7纳米用科学记数法表示为（）

A、 $0.7 \times 10^{- 8}$ 米 B、 $0.7 \times 10^{- 9}$ 米 C、 $7 \times 10^{- 8}$ 米 D、 $7 \times 10^{- 9}$

查看试题解析
3. 如图，下面哪个条件能判断DE∥BC的是（）

A、∠1＝∠2 B、∠4＝∠C C、∠1+∠3＝180° D、∠3+∠C＝180°

查看试题解析
4. 下列分解因式正确的是（）

A、 $- a + a^{3} = - a (1 + a^{2})$ B、 $2 a - 4 b + 2 = 2 (a - 2 b)$ C、 $a^{2} - 4 = {(a - 2)}^{2}$ D、 $a^{2} - 2 a + 1 = {(a - 1)}^{2}$

查看试题解析
5. 如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则CF的长为（）

A、3 B、4 C、5 D、6

查看试题解析
6. 若二元一次方程组 ${\begin{array}{l} a x + b y = 4 \\ b x + a y = 5 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则的值是（）

A、9 B、6 C、3 D、1

查看试题解析
7. 若2x+m与x+3的乘积中不含x的一次项，则m的值为（）

A、﹣6 B、0 C、﹣2 D、3

查看试题解析
8. 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重.问：每只雀、燕的重量各为多少?设一只雀的重量为x斤，一只燕的重量为y斤，则可列方程组为（）

A、 ${\begin{cases} 5 x + 6 y = 1 \\ 5 x - y = 6 y - x \end{cases}$ B、 ${\begin{cases} 6 x + 5 y = 1 \\ 5 x + y = 6 y + x \end{cases}$ C、 ${\begin{cases} 5 x + 6 y = 1 \\ 4 x + y = 5 y + x \end{cases}$ D、 ${\begin{cases} 6 x + 5 y = 1 \\ 4 x - y = 5 y - x \end{cases}$

查看试题解析
9. 如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB、CD，若CD∥BE，∠1＝40°，则∠2的度数是（）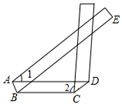

A、90° B、100° C、105° D、110°

查看试题解析
10. 有4张长为a、宽为b（a＞b）的长方形纸片，按如图的方式拼成一个边长为（a+b）的正方形，图中阴影部分的面积为S₁ ，空白部分的面积为S₂.若S₁＝ $\frac{1}{2}$ S₂ ，则a、b满足（）

A、2a＝3b B、2a＝5b C、a＝2b D、a＝3b

查看试题解析

二、填空题（每小题3分，共18分）

11. 因式分解m³﹣4m＝.

查看试题解析
12. 已知方程x+2y＝3，用关于x的代数式表示y，则y＝.．

查看试题解析
13. 如图所示，在一块长为a米，宽为b米的长方形草地上，有两条宽都为1米的纵、横相交的小路，这块草地的绿地面积为.平方米．

查看试题解析
14. 如图所示，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的补角，若∠1=32°，∠3=60°，则∠2等于.

查看试题解析
15. 如果多项式x²﹣2（m+1）xy+16y²是个完全平方式，则m＝.

查看试题解析
16. 已知关于x，y的方程组 ${\begin{matrix} x + 2 y = k \\ 2 x + 3 y = 3 k - 1 \end{matrix}$ ，给出下列结论：①当K=2时， ${\begin{matrix} x = 4 \\ y = - 1 \end{matrix}$ 是方程组的解；②当k＝ $\frac{1}{2}$ 时，x，y的值互为相反数；③2^x•8^y＝2^z ，则z＝1；④若方程组的解也是方程x+y＝2﹣k的解，则k＝1.其中正确的是（填写正确结论的序号）.

查看试题解析

三、解答题（有7题，共52分）

17. 解方程组：

(1)、 ${\begin{cases} 2 x - y = 5 \\ - x - y = 2 \end{cases}$

(2)、 ${\begin{cases} x - y = 3 (x + y) \\ 2 (x - y) + x + y = 7 \end{cases}$

(3)、计算： ${(- 4)}^{2} + {(- 1)}^{2020} \times {(3 - π)}^{0} - {(- \frac{1}{5})}^{- 2}$

查看试题解析
18. 先化简，再求值：(2x-1)²-(2x+1)(2x-1)+(x+1)(3-x)，其中x= $\frac{5}{2}$ 。

查看试题解析
19. 如图，在正方形网格中有一个△ABC（点A，B，C都在网格格点上），按要求完成下列各题．

(1)、将△ABC向右平移5格，向上平移2格，请在网格图中画出经平移后得到的△A′B′C′（点A与A′对应）．

(2)、在（1）的基础上，连结AA′，BA′，则图中△ABA′的面积为．

查看试题解析
20. 如图，在△ABC中，点D、E分别在BC、AB上，且EF∥AD，∠1+∠2= 180°．

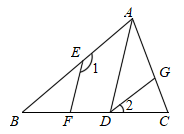(1)、试猜想∠2与∠BAD的关系，并说明理由；

(2)、若DG平分∠ADC，说明：DG∥AB。

查看试题解析
21. 为了响应国家与新冠疫情斗争的号召，某校通过悬挂横幅与宣传牌进行专项宣传活动。已知制作5条横幅与制作2块宣传牌的费用一样，制作2条横幅与3块宣传牌共需950元.

(1)、求制作横幅与宣传牌的单价各是多少？

(2)、学校计划共用2500元制作横幅和宣传牌，要求宣传牌不少于5块，请问：可以几种设计制作方案？（横幅和宣传牌都要有）

查看试题解析
22. 数学活动课上，老师准备了若干张如图1所示的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b、宽为a的长方形．现在用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2所示的大正方形．观察图形并解答下列问题．

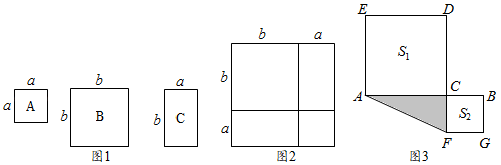(1)、由图1到图2的过程可得到的因式分解等式为（用含a，b的代数式表示）；

(2)、小敏用图1中的A、B、C三种纸片拼出一个面积为(2a+b)(a+2b)的大长方形，求需要A、B、C三种纸片各多少张；

(3)、如图3，C为线段AB上的动点，分别以AC，BC为边在AB的两侧作正方形ACDE和正方形BCFG．若AB=6，记正方形ACDE和正方形BCFG的面积分别为S₁ ， S₂ ，且S₁+S₂=20，利用（1）中的结论求图中三角形ACF的面积．

查看试题解析
23. 已知 $△ A B C$ ， $D E / / A B$ 交AC于点E， $D F / / A C$ 交AB于点F．

(1)、如图1，若点D在边BC上，
①补全图形；
②求证： $∠ A = ∠ E D F$ ．

(2)、点G是线段AC上的一点，连接FG，DG．
①若点G是线段AE的中点，请你在图2中补全图形，判断 $∠ A F G$ ， $∠ E D G$ ， $∠ D G F$ 之间的数量关系，并证明；
②若点G是线段EC上的一点，请你直接写出 $∠ A F G$ ， $∠ E D G$ ， $∠ D G F$ 之间的数量关系．

查看试题解析