贵州省贵阳市2022届高三理数适应性考试试卷(二)
试卷更新日期:2022-05-16 类型:高考模拟
一、单选题
-
1. 设全集 , 集合 , , 则( )A、 B、 C、 D、2. 已知为虚数单位,复数满足 , 则( )A、2 B、 C、-2 D、3. 若展开式中存在常数项,则正整数n的最小值是( )A、5 B、6 C、7 D、84. 2021年11月24日,贵阳市修文县发生了4.6级地震,所幸的是没有人员伤亡和较大财产损失,在抗震分析中,某结构工程师提出:由于实测地震记录的缺乏,且考虑到强震记录数量的有限性和地震动的不可重复性,在抗震分析中还需要人工合成符合某些指定统计特征的非平稳地震波时程,其中地震动时程强度包络函数 , (单位:秒)分别为控制强震平稳段的首末时刻;(单位:秒)表示地震动总持时;是衰减因子,控制下降段衰减的快慢.在一次抗震分析中,地震动总持时是20秒,控制强震平稳段的首末时刻分别是5秒和10秒,衰减因子是0.2,则当秒时,地震动时程强度包络函数值是( )A、 B、1 C、9 D、5. 函数的图像大致为( )A、
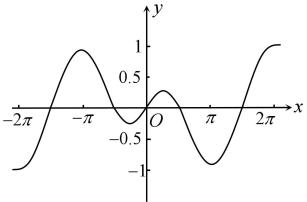 B、
B、 C、
C、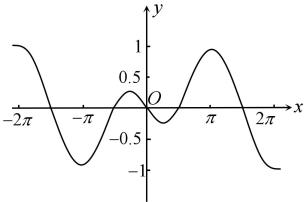 D、
D、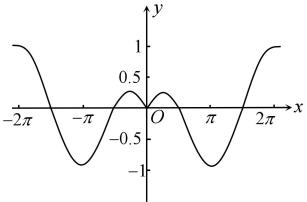 6. 已知为双曲线的焦点,过作轴的垂线交于点 , 且 , 则的渐近线方程是( )A、 B、 C、 D、7. 已知、表示两条不同的直线,表示平面,则下面四个命题正确的是( )
6. 已知为双曲线的焦点,过作轴的垂线交于点 , 且 , 则的渐近线方程是( )A、 B、 C、 D、7. 已知、表示两条不同的直线,表示平面,则下面四个命题正确的是( )①若 , , 则;②若 , , 则;③若 , , 则;④若 , , 则 .
A、①② B、②③ C、①③ D、③④8. 下列命题为真命题的是( )A、若数据 , , , …,的方差为3,则数据的方差为5; B、对具有线性相关关系的变量x,y,其线性回归方程为 , 若样本点的中心为 , 则实数m的值是4; C、若随机变量X服从正态分布 , , 则; D、若随机变量X服从二项分布 , , 则 .9. 已知函数在内单调递增,则在内的零点个数最多为( )A、3 B、4 C、5 D、610. 已知直线和与圆都相切,则圆的面积的最大值是( )A、2π B、4π C、8π D、16π11. 已知抛物线的准线交轴于点 , 过点作直线交于 , 两点,且 , 则直线的斜率是( )A、 B、 C、 D、12. 秦九韶是我国南宋数学家,其著作《数书九章》中的大衍求一术、三斜求积术和秦九韶算法是具有世界意义的重要贡献.秦九韶把三角形的三条边分别称为小斜、中斜和大斜,三斜求积术即已知三边长求三角形面积的方法,用公式表示为: , 其中 , , 是的内角 , , 的对边.已知中, , 则面积的最大值为( )A、 B、 C、 D、二、填空题
-
13. 若 , 满足约束条件 , 则的最大值是 .14. 已知向量 , , 则 .15. 已知定义在上的函数满足 , 且当时, , 若的值域为 , 则实数的取值范围为 .16. 球O是棱长为1的正方体的内切球,球与面、面、面、球O都相切,则球的表面积是 .
三、解答题
-
17. 已知首项为1的等差数列的前项和为 , 若成等比数列.(1)、求和:(2)、求证:18. 在棱柱中,底面为平行四边形,为线段上一动点.
 (1)、证明:平面;(2)、若平面A1B1C1D1 , , , , 求二面角的余弦值.19. 2021年7月24日,在奥运会女子个人重剑决赛中,中国选手孙一文在最后关头一剑封喉,斩获金牌,掀起了新一轮“击剑热潮”.甲、乙、丙三位重剑爱好者决定进行一场比赛,每局两人对战,没有平局,已知每局比赛甲赢乙的概率为 , 甲赢丙的概率为 , 丙赢乙的概率为 . 因为甲是最弱的,所以让他决定第一局的两个比赛者(甲可以选定自己比赛,也可以选定另外两个人比赛),每局获胜者与此局未比赛的人进行下一局的比赛,在比赛中某人首先获胜两局就成为整个比赛的冠军,比赛结束.(1)、若甲指定第一局由乙丙对战,求“只进行三局甲就成为冠军”的概率;(2)、请帮助甲进行第一局的决策(甲乙、甲丙或乙丙比赛),使得甲最终获得冠军的概率最大.20. 已知椭圆的离心率为 , 右焦点是 , 左、右顶点分别是和 . 直线与椭圆交于 , 两点,点在轴上方,且当时, .(1)、求椭圆的方程;(2)、若直线、的斜率分别是和 , 求的取值范围.
(1)、证明:平面;(2)、若平面A1B1C1D1 , , , , 求二面角的余弦值.19. 2021年7月24日,在奥运会女子个人重剑决赛中,中国选手孙一文在最后关头一剑封喉,斩获金牌,掀起了新一轮“击剑热潮”.甲、乙、丙三位重剑爱好者决定进行一场比赛,每局两人对战,没有平局,已知每局比赛甲赢乙的概率为 , 甲赢丙的概率为 , 丙赢乙的概率为 . 因为甲是最弱的,所以让他决定第一局的两个比赛者(甲可以选定自己比赛,也可以选定另外两个人比赛),每局获胜者与此局未比赛的人进行下一局的比赛,在比赛中某人首先获胜两局就成为整个比赛的冠军,比赛结束.(1)、若甲指定第一局由乙丙对战,求“只进行三局甲就成为冠军”的概率;(2)、请帮助甲进行第一局的决策(甲乙、甲丙或乙丙比赛),使得甲最终获得冠军的概率最大.20. 已知椭圆的离心率为 , 右焦点是 , 左、右顶点分别是和 . 直线与椭圆交于 , 两点,点在轴上方,且当时, .(1)、求椭圆的方程;(2)、若直线、的斜率分别是和 , 求的取值范围.