贵州省毕节市2022届高三理数诊断性考试试卷(三)
试卷更新日期:2022-05-16 类型:高考模拟
一、单选题
-
1. 已知全集 , 集合 , 若图中阴影部分表示的集合是 , 则集合( )
 A、 B、 C、 D、2. 已知复数在复平面内对应的点与复数在复平面内对应的点关于虚轴对称,则复数的共轭复数( )A、 B、 C、 D、3. 20世纪70年代,里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级 , 其计算公式为 , 其中是被测地震的最大振幅,是“标准地震”的振幅.假设在一次地震中,一个距离震中千米的测震仪记录的地震最大振幅是 , 此时标准地震的振幅是 , 计算这次地震的震级为( )A、4 B、5 C、6 D、74. 已知正项等比数列中,其前项和为 , 若 , , 则公比的值为( )A、2 B、 C、2或 D、2或5. 设有下列四个命题:
A、 B、 C、 D、2. 已知复数在复平面内对应的点与复数在复平面内对应的点关于虚轴对称,则复数的共轭复数( )A、 B、 C、 D、3. 20世纪70年代,里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级 , 其计算公式为 , 其中是被测地震的最大振幅,是“标准地震”的振幅.假设在一次地震中,一个距离震中千米的测震仪记录的地震最大振幅是 , 此时标准地震的振幅是 , 计算这次地震的震级为( )A、4 B、5 C、6 D、74. 已知正项等比数列中,其前项和为 , 若 , , 则公比的值为( )A、2 B、 C、2或 D、2或5. 设有下列四个命题::“ , 使得”的否定是“ , 都有”;
:若函数是奇函数,则必有;
:函数的图象可由的图象向右平移2个单位得到;
:若幂函数的图象与坐标轴没有公共点,则 .
则下述命题中真命题是( )
A、 B、 C、 D、6. 已知50个产品中,有35个产品长度合格,45个产品质量合格,20个产品长度和质量都合格,现任取一个产品,若它的质量合格,则它的长度也合格的概率为( )A、 B、 C、 D、7. 已知向量是非零向量,λ、 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件8. 在正四棱锥中,底面边长为 , 侧棱长为4,点P是底面ABCD内一动点,且 , 则当A,P两点间距离最小时,直线BP与直线SC所成角的余弦值为( )A、 B、 C、 D、9. 曲线与直线有两个交点,则实数的取值范围为( )A、 B、 C、 D、10. 在长方体中,点 , 分别是棱 , 的中点,点为对角线 , 的交点,若平面平面 , , 且 , 则实数( )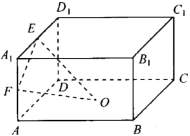 A、 B、 C、 D、11. 已知 , , (为自然对数的底数),则 , , 的大小关系为( )A、 B、 C、 D、12. 已知 , 是椭圆的左、右焦点,是椭圆的左顶点,点在过且斜率为的直线上,为等腰三角形, , 则椭圆的离心率为( )A、 B、 C、 D、
A、 B、 C、 D、11. 已知 , , (为自然对数的底数),则 , , 的大小关系为( )A、 B、 C、 D、12. 已知 , 是椭圆的左、右焦点,是椭圆的左顶点,点在过且斜率为的直线上,为等腰三角形, , 则椭圆的离心率为( )A、 B、 C、 D、二、填空题
-
13. 二项式的展开式中的系数为(用数字作答).14. 已知 , 是双曲线的左、右焦点,为右支上一点,若 , 则双曲线经过一、三象限的渐近线的斜率的取值范围为 .15. 已知函数在有且仅有3个零点,则的取值范围为 .16. 定义:若有穷数列 , , …, , 满足 , , …, , 即( , 且),则称该数列为“对称数列”.若数列是项数为的对称数列,且 , , …,构成首项为 , 公差为的等差数列,记数列的前项的和为 , 则取得最大值时的值为 .
三、解答题
-
17. 在锐角中,角A, , 的对边分别为 , , , 满足 .(1)、求角;(2)、若 , 求中边上的高的最大值.18. 甲、乙两名选手争夺一场比赛的冠军.比赛采取五局三胜制,即某选手率先获得三局胜利时比赛结束,且该选手夺得冠军.根据两人以往对战的经历,甲乙在一局比赛中获胜的概率分别为和 , 没有平局且每局比赛的结果相互独立.(1)、求经过四局比赛且甲夺得冠军的概率;(2)、若每场比赛获胜的一方得2分,失败的一方得分.设比赛结束时甲的得分为X,求随机变量X的分布列与数学期望.19. 如图,在四棱锥中, , △是边长为2的正三角形,平面PCD⊥平面ABCD, , 点E,F,H分别是线段PB,PC,AB的中点.
 (1)、求证:点H在平面DEF内;(2)、若二面角的余弦值为 , 求三棱锥的体积.20. 已知抛物线的焦点为 , 且点与上点的距离的最大值为 .(1)、求;(2)、当时,设 , , 是抛物线上的三个点,若直线 , 均与相切,求证:直线与相切.
(1)、求证:点H在平面DEF内;(2)、若二面角的余弦值为 , 求三棱锥的体积.20. 已知抛物线的焦点为 , 且点与上点的距离的最大值为 .(1)、求;(2)、当时,设 , , 是抛物线上的三个点,若直线 , 均与相切,求证:直线与相切.