安徽省宿州市十三所重点中学 2021-2022学年高一下学期数学期中联考试卷

试卷更新日期：2022-05-16 类型：期中考试

进入出卷网下载

一、单选题

1. 将210°化成弧度为（）

A、 $- \frac{5 π}{6}$ B、 $\frac{5 π}{6}$ C、 $\frac{4 π}{3}$ D、 $\frac{7 π}{6}$

查看试题解析
2. 在 $△ A B C$ 中，设 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ， $D$ 为边 $B C$ 上靠近 $C$ 的一个三等分点，则 $\vec{A D} =$ （）

A、 $\frac{1}{2} (\vec{a} + \vec{b})$ B、 $\frac{1}{3} \vec{a} + \frac{2}{3} \vec{b}$ C、 $\frac{4}{3} \vec{a} - \frac{1}{3} \vec{b}$ D、 $\frac{4}{3} \vec{b} - \frac{1}{3} \vec{a}$

查看试题解析
3. 下列各式的符号为正的是（）

A、 $c o s 3$ B、 $s i n \frac{5 π}{3} c o s (- \frac{π}{6})$ C、 $s i n 2 - c o s 2$ D、 $t a n \frac{7 π}{8}$

查看试题解析
4. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，且 $b^{2} = a^{2} + c^{2} + a c$ ，则 $B =$ （）

A、 $\frac{π}{6}$ B、 $\frac{3 π}{4}$ C、 $\frac{5 π}{6}$ D、 $\frac{2 π}{3}$

查看试题解析
5. 菱形 $A B C D$ 的边长为2，且 $∠ D A B = 60 °$ ， $\vec{A B} \cdot \vec{B C} =$ （）

A、 $\sqrt{3}$ B、-2 C、2 D、 $- \sqrt{3}$

查看试题解析
6. 砀山被誉为“酥梨之乡”，每逢四月，万树梨花开，游客八方来．如图1，梨花广场的标志性建筑就是根据梨花的形状进行设计的，建筑的五个“花瓣”中的每一个都可以近似看作由两个对称的弓形组成，图2为其中的一个“花瓣”平面图，设弓形的圆弧所在圆的半径为 $R$ ，弦长为 $\sqrt{2} R$ ，则一个“花瓣”的面积为（）

A、 $\frac{π - 1}{2} R^{2}$ B、 $\frac{π - 2}{2} R^{2}$ C、 $\frac{π - 1}{4} R^{2}$ D、 $(π - 1) R^{2}$

查看试题解析
7. 函数 $f (x) = \frac{s i n x}{1 + c o s x}$ 的部分图象大致为（）

A、 B、 C、 D、

查看试题解析
8. 公元263，魏晋时期的数学家刘徽借助圆内接正多边形计算圆的面积，其“割圆术”思想为：割之弥细，所失弥少，割之又割，以至不可割，则与圆周合体．某数学兴趣小组，分别计算单位圆内接正 $n$ 边形和外切正 $n$ 边形（各边都和圆相切）的面积，将它们的平均数作为圆的面积，则用此法求得圆面积为（）

A、 $n (s i n \frac{180 °}{n} c o s \frac{180 °}{n} + t a n \frac{180 °}{n})$ B、 $\frac{1}{2} n (s i n \frac{180 °}{n} c o s \frac{180 °}{n} + t a n \frac{180 °}{n})$ C、 $n (s i n \frac{360 °}{n} c o s \frac{360 °}{n} + t a n \frac{360 °}{n})$ D、 $\frac{1}{2} n (s i n \frac{360 °}{n} c o s \frac{360 °}{n} + t a n \frac{360 °}{n})$

查看试题解析

二、多选题

9. 下列说法正确的是（）

A、终边相同的角的同一三角函数值一定相同 B、 $α \in (0 ， \frac{π}{2})$ ，则 $t a n α + \frac{1}{t a n α}$ 的最小值为 $2 \sqrt{2}$ C、已知 $| \vec{a} | = 2$ ， $| \vec{b} | = 1$ ， $⟨ \vec{a} ， \vec{b} ⟩ = 135 °$ ，则 $\vec{a}$ 在 $\vec{b}$ 上的投影数量为 $- \sqrt{2}$ D、非零向量 $\vec{a}$ ， $\vec{b}$ ， $\vec{c}$ ，若 $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{c}$ ，则 $\vec{a} = \vec{c}$

查看试题解析
10. 要得到如图所示图象，可由 $f (x) = s i n x$ 图象经过怎样的变换得到（）

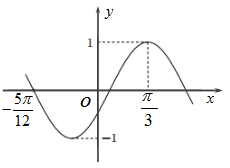A、每个点横坐标缩短为原来的 $\frac{1}{2}$ ，纵坐标不变，再将横坐标向右平移 $\frac{11 π}{12}$ 个单位，纵坐标不变 B、每个点横坐标缩短为原来的 $\frac{1}{2}$ ，纵坐标不变，再将横坐标向右平移 $\frac{π}{12}$ 个单位，纵坐标不变 C、横坐标向右平移 $\frac{π}{6}$ 个单位，纵坐标不变，再将每个点横坐标缩短为原来的 $\frac{1}{2}$ ，纵坐标不变 D、横坐标向左平移 $\frac{23 π}{6}$ 个单位，纵坐标不变，再将每个点横坐标缩短为原来的 $\frac{1}{2}$ ，纵坐标不变

查看试题解析
11. 已知函数 $f (x) = s i n ω x$ （ $ω > 0$ ）在 $(- \frac{π}{6} ， \frac{π}{6})$ 上单调，则 $ω$ 的可能值为（）

A、2 B、3 C、4 D、5

查看试题解析
12. 定义在 $R$ 上的函数 $y = f (x)$ 满足在 $(0 ， 1]$ 上单调递增， $f (3 + x) = f (3 - x)$ ，且图象关于点 $(4 ， 0)$ 对称，则下列选项正确的是（）

A、 $f (0) = 0$ B、 $f (2020) < f (2021) < f (2022)$ C、 $y = f (x)$ 在 $[1 ， 3]$ 上单调 D、函数 $f (x)$ 在 $[0 ， 2022]$ 上可能有2023个零点

查看试题解析

三、填空题

13. 向量 $\vec{a} = (2 ， 3)$ ， $\vec{b} = (x ， 5)$ ，且 $\vec{a} ∥ \vec{b}$ ，则 $x =$ ．

查看试题解析
14. 函数 $y = - 2 t a n^{2} x + 3 t a n x - 1$ ， $x \in [- \frac{π}{4} ， \frac{π}{4}]$ 的值域为．

查看试题解析
15. 已知 $c o s (α + \frac{π}{6}) = - \frac{3}{4}$ ，则 $c o s (α - \frac{5 π}{6}) + s i n (α - \frac{π}{3}) =$ ．

查看试题解析
16. 某同学为测量数学楼的高度，先在地面选择一点 $C$ ，测量出对教学楼 $A B$ 的仰角 $∠ A C B = α$ ，再分别执行如下四种测量方案，则利用测量数据可表示出教学楼高度的方案编号为．
方案（1）：从点 $C$ 向教学楼前进 $a$ 米到达点 $D$ ，测量出角 $∠ A D B = β$ ；
方案（2）：在地面上另选点 $D$ ，测量出角 $∠ A C D = β$ ， $∠ A D C = γ$ ， $C D = a$ 米；
方案（3）：在地面上另选点 $D$ ，测量出角 $∠ B D C = β$ ， $C D = a$ 米；
方案（4）：从过点 $C$ 的直线上（不过点 $B$ ）另选点 $D$ 、 $E$ ，测量出 $C D = 2 D E = a$ 米， $∠ A D B = β$ ， $∠ A E B = γ$ ．

查看试题解析

四、解答题

17. 已知角 $α$ 终边上一点 $(- 4 ， m)$ ， $m > 0$ ，且 $c o s α = - \frac{4}{5}$ ．

(1)、求 $m$ 的值；

(2)、求 $\frac{t a n (π - α) \cdot s i n (π - α) \cdot s i n (\frac{π}{2} - α)}{c o s (π + α)}$ 的值．

查看试题解析
18. 已知 $| \vec{a} | = 2$ ， $| \vec{b} | = \sqrt{3}$ ，向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为150°．

(1)、计算 $| \vec{a} + 2 \vec{b} |$ ；

(2)、若 $(\vec{a} + 3 λ \vec{b}) ⊥ (\vec{a} + λ \vec{b})$ ，求实数 $λ$ 的值．

查看试题解析
19. 已知函数 $f (x) = 2 s i n (2 x - \frac{π}{3})$ ．

(1)、用“五点（画图）法”作出 $f (x)$ 在 $x \in [0 ， π]$ 的简图；

(2)、求函数 $f (x)$ 的单调递减区间．

查看试题解析
20. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，且 $\sqrt{3} a s i n C = c c o s A$ ， $a = 3$ ．

(1)、求 $A$ 大小；

(2)、若 $B C$ 边上的中线长为 $\frac{\sqrt{21}}{2}$ ，求 $△ A B C$ 的面积．

查看试题解析
21. 已知 $△ A B C$ 中， $A = 60 °$ ， $A B = 1$ ， $A C = 4$ ， $\vec{A E} = λ \vec{A C}$ （ $0 < λ < 1$ ）．

(1)、求 $| \vec{B E} |$ 的取值范围；

(2)、若线段 $B E$ 上一点 $D$ 满足 $\vec{A D} = μ (\frac{\vec{A B}}{| \vec{A B} |} + \frac{\vec{A C}}{| \vec{A C} |})$ ，求 $s i n ∠ A D B = \frac{7 \sqrt{2}}{10}$ 的最小值．

查看试题解析
22. 已知函数 $f (x) = 2 s i n (ω x + φ)$ （ $ω > 0$ ， $| φ | < π$ ），其图象一条对称轴与相邻对称中心的横坐标相差 $\frac{π}{4}$ ， ____；从以下两个条件中任选一个补充在空白横线中．
①函数 $f (x)$ 向左平移 $\frac{π}{6}$ 个单位得到的图象关于 $y$ 轴对称且 $f (0) < 0$ ．
②函数 $f (x)$ 的一条对称轴为 $x = - \frac{π}{3}$ 且 $f (\frac{π}{6}) < f (1)$ ；

(1)、求函数 $f (x)$ 的解析式；

(2)、若 $x \in [\frac{π}{2} ， \frac{17 π}{12}]$ ，方程 $f^{2} (x) + (4 - a) f (x) + 3 - a = 0$ 存在4个不相等的实数根，求实数 $a$ 的取值范围．

查看试题解析