2022年5月湖北省黄冈市中考全真模拟试题(1)
试卷更新日期:2022-05-15 类型:中考模拟
一、单选题
-
1. 在四个数中,最小的是( )A、-3 B、0 C、 D、-12. 如图所示的几何体是由6个大小相同的小正方体组成,它的主视图为( )
 A、
A、 B、
B、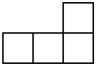 C、
C、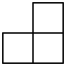 D、
D、 3. 2021年12月9日,“天宫课堂”第一课正式开讲,时隔8年之后,中国航天员再次进行太空授课,此时空间站距离地球约370000米,数据370000用科学记数法表示为( )A、 B、 C、 D、4. 计算的正确结果是( )A、 B、 C、 D、5. 若扇形的圆心角为 , 半径为3,则该扇形的面积为( )A、 B、 C、 D、6. 如图,小华在屋顶D点时,测得对面图书馆顶部B的仰角为 , 图书馆底部A的俯角为 , 若这两幢楼的距离米,则图书馆楼高等于( )
3. 2021年12月9日,“天宫课堂”第一课正式开讲,时隔8年之后,中国航天员再次进行太空授课,此时空间站距离地球约370000米,数据370000用科学记数法表示为( )A、 B、 C、 D、4. 计算的正确结果是( )A、 B、 C、 D、5. 若扇形的圆心角为 , 半径为3,则该扇形的面积为( )A、 B、 C、 D、6. 如图,小华在屋顶D点时,测得对面图书馆顶部B的仰角为 , 图书馆底部A的俯角为 , 若这两幢楼的距离米,则图书馆楼高等于( )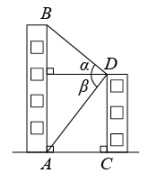 A、米 B、米 C、米 D、米7. 某校操场上学生体育运动情况的统计图如图所示.若该校操场上跳绳的学生有45人,则踢足球的学生有( )
A、米 B、米 C、米 D、米7. 某校操场上学生体育运动情况的统计图如图所示.若该校操场上跳绳的学生有45人,则踢足球的学生有( ) A、90人 B、75人 C、60人 D、30人8. 如图是中国古代数学家赵爽用来证明勾股定理的弦图示意图,它是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形 , 连结并延长交于点P.若 , 则的长为( )
A、90人 B、75人 C、60人 D、30人8. 如图是中国古代数学家赵爽用来证明勾股定理的弦图示意图,它是由四个全等的直角三角形和一个小正方形组成,恰好拼成一个大正方形 , 连结并延长交于点P.若 , 则的长为( ) A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题
-
9. 若 ,则 .10. 小明上学期平时测验,期中考试和期末考试的数学成绩分别是95分、90分、94分.如果这3项成绩分别按 、 、 的比例计算,那么小明上学期的数学平均分是.11. 如图,已知⊙O上有三点A、B、C,半径OC=2,∠ABC=30°,切线AP交OC延长线于点P,则△OAP的周长为
 12. 如图,在菱形中, , 过A,B,C三点的圆交的延长线于点E,连结 , 则度.
12. 如图,在菱形中, , 过A,B,C三点的圆交的延长线于点E,连结 , 则度.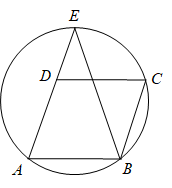 13. 如图,位于平面直角坐标系中,点B在x轴正半轴上,点A及的中点D在反比例函数的图象上,点C在反比例函数的图象上,则k的值为.
13. 如图,位于平面直角坐标系中,点B在x轴正半轴上,点A及的中点D在反比例函数的图象上,点C在反比例函数的图象上,则k的值为. 14. 如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以12千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞至村庄C的正上方A处时,测得∠NAD=60°,该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°,则村庄C、D间的距离为千米.( ≈1.732,结果保留一位小数)
14. 如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以12千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞至村庄C的正上方A处时,测得∠NAD=60°,该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°,则村庄C、D间的距离为千米.( ≈1.732,结果保留一位小数) 15. 如图所示,将形状大小完全相同的“
15. 如图所示,将形状大小完全相同的“ ”按照一定的规律摆成下列图形:第1幅图中“
”按照一定的规律摆成下列图形:第1幅图中“  ”的个数为 ,第2幅图中“
”的个数为 ,第2幅图中“  ”的个数为 ,第3幅图中“
”的个数为 ,第3幅图中“  ”的个数为 ,…,以此类推.
”的个数为 ,…,以此类推. 


 (1)、按照图中规律, ;(2)、 .16. 如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2-6ax+5a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧,连接BD,则BD的最小值是.
(1)、按照图中规律, ;(2)、 .16. 如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2-6ax+5a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧,连接BD,则BD的最小值是.
三、综合题
-
17.(1)、(x+2y)2﹣y(x+4y);(2)、(﹣1)÷ .18. 小亮是个集邮爱好者,他收集了如图所示的四张纪念邮票(除正面内容不同外,其余均相同),现将四张邮票背面朝上,洗匀放好
 (1)、小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)19. 随着信息技术的迅猛发展,人们购物的支付方式更加多样、便捷,为调查大学生购物支付方式,某大学一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、小亮从中随机抽取一张邮票是“冬奥会吉祥物冰墩墩”的概率是(2)、小亮从中随机抽取一张邮票(不放回),再从余下的邮票中随机抽取一张,求抽到的两张邮票恰好是“冬奥会会徽”和“冬奥会吉祥物冰墩墩”的概率.(这四张邮票从左到右依次分别用字母A、B、C、D表示)19. 随着信息技术的迅猛发展,人们购物的支付方式更加多样、便捷,为调查大学生购物支付方式,某大学一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为(2)、将条形统计图补充完整;(3)、若该大学有10000名学生,请你估计购物选择用支付宝支付方式的学生约有多少人?20. 冰墩墩(如图)是2022年北京冬季奥运会的吉祥物.某商店第一次用1200元购进冰墩墩手办若干个,第二次又用相同价格购进冰墩墩饰扣若干个,已知每个冰墩墩饰扣的进价是冰墩墩手办进价的 , 购进冰墩墩手办数量比饰扣少了10个.
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为(2)、将条形统计图补充完整;(3)、若该大学有10000名学生,请你估计购物选择用支付宝支付方式的学生约有多少人?20. 冰墩墩(如图)是2022年北京冬季奥运会的吉祥物.某商店第一次用1200元购进冰墩墩手办若干个,第二次又用相同价格购进冰墩墩饰扣若干个,已知每个冰墩墩饰扣的进价是冰墩墩手办进价的 , 购进冰墩墩手办数量比饰扣少了10个. (1)、冰墩墩饰扣的进价是多少元?(2)、若冰墩墩饰扣的售价要比冰墩墩手办的售价少30元,且销售完毕后获利不低于1100元,问每个冰墩墩手办的售价至少是多少元?21. 如图,点P为函数与函数图象的交点,点P的纵坐标为4,轴,垂足为点B.
(1)、冰墩墩饰扣的进价是多少元?(2)、若冰墩墩饰扣的售价要比冰墩墩手办的售价少30元,且销售完毕后获利不低于1100元,问每个冰墩墩手办的售价至少是多少元?21. 如图,点P为函数与函数图象的交点,点P的纵坐标为4,轴,垂足为点B. (1)、求m的值;(2)、点M是函数图象上一动点,过点M作于点D,若 , 求点M的坐标.22. 如图1,在中, , AB是的直径,交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是的切线.
(1)、求m的值;(2)、点M是函数图象上一动点,过点M作于点D,若 , 求点M的坐标.22. 如图1,在中, , AB是的直径,交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,PD是的切线.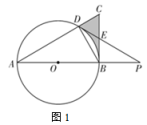 (1)、求证:;(2)、若 , , 求图中阴影部分的周长和面积;(3)、如图2, , 连接DM,交AB于点N,若 , 求的值.
(1)、求证:;(2)、若 , , 求图中阴影部分的周长和面积;(3)、如图2, , 连接DM,交AB于点N,若 , 求的值.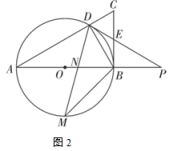 23. 某体育器材专卖店销售A,B两款篮球,已知A款篮球的销售单价比B款篮球多10元,且用4000元购买A款篮球的数量与用3600元购买B款篮球的数量相同.(1)、A、B两款篮球的销售单价各是多少元?(2)、由于需求量大,A、B两款篮球很快售完,该专卖店计划再次购进这两款篮球共100个,且A款篮球的数量不少于B款篮球数量的2倍.
23. 某体育器材专卖店销售A,B两款篮球,已知A款篮球的销售单价比B款篮球多10元,且用4000元购买A款篮球的数量与用3600元购买B款篮球的数量相同.(1)、A、B两款篮球的销售单价各是多少元?(2)、由于需求量大,A、B两款篮球很快售完,该专卖店计划再次购进这两款篮球共100个,且A款篮球的数量不少于B款篮球数量的2倍.①求A款篮球至少有几个;
②老板计划让利顾客,A款篮球8折出售,B款篮球的销售单价不变,且两款篮球的进价每个均为60元,应如何进货才能使这批篮球的销售利润最大,最大利润是多少元?
24. 定义:四边形ABCD中,AB=AC,∠BDC=∠BAC,则称四边形ABCD为半角四边形,边BC称为半对边. (1)、如图①,若四边形ABCD为半角四边形,且BC为半对边,设∠DBC=α,用含有α的代数式表示∠ACD;(2)、如图②,等腰△ABC,AB=AC,点D为其内部一点,∠ABD=∠ACD,连结AD,作△ACD的外接圆⊙O,BD的延长线交⊙O于点E,连结EA,EC,求证:四边形ABCE为半角四边形;(3)、如图③,在(2)的条件下,延长BA交⊙O于点F,连结EF,EF∥BC.
(1)、如图①,若四边形ABCD为半角四边形,且BC为半对边,设∠DBC=α,用含有α的代数式表示∠ACD;(2)、如图②,等腰△ABC,AB=AC,点D为其内部一点,∠ABD=∠ACD,连结AD,作△ACD的外接圆⊙O,BD的延长线交⊙O于点E,连结EA,EC,求证:四边形ABCE为半角四边形;(3)、如图③,在(2)的条件下,延长BA交⊙O于点F,连结EF,EF∥BC.①求证:BC=CE;
②若AD=3,BC=6 , 求四边形ADEF的面积.
25. 如图1,抛物线y=﹣x2+bx+c经过点A(﹣1,0)、B(3,0). (1)、求抛物线的函数表达式:(2)、设抛物线的顶点为D,与y轴相交与点C,连接AC、CD、BC、BD,请你判断∠ACO与∠DBC的数量关系,并说明理由;(3)、如图2,连接AD,与BC相交于点E,点G是抛物线上一动点,在对称轴上是否存在点F,使得∠EFG=90°,且tan∠FEG=如果存在,请求出点F的坐标;如果不存在,请说明理由.
(1)、求抛物线的函数表达式:(2)、设抛物线的顶点为D,与y轴相交与点C,连接AC、CD、BC、BD,请你判断∠ACO与∠DBC的数量关系,并说明理由;(3)、如图2,连接AD,与BC相交于点E,点G是抛物线上一动点,在对称轴上是否存在点F,使得∠EFG=90°,且tan∠FEG=如果存在,请求出点F的坐标;如果不存在,请说明理由.