2022年甘肃省兰州市中考数学模拟试卷二（5月份）

试卷更新日期：2022-05-13 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共30分）

1. 2019 年 9 月 8 日至 16 日，中华人民共和国第十届少数民族传统体育运动会在郑州市举行.运动会期间，公交运营车次 476208 次，完成运营里程 742 万公里.742 万用科学记数法表示为（）

A、 7.42x10² B、7.42x10⁵ C、7.42x10⁶ D、7.42x10⁷

查看试题解析
2. 下列命题，其中是真命题的为（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、一组邻边相等的矩形是正方形 C、对角线相等的四边形是矩形 D、对角线互相垂直的四边形是菱形

查看试题解析
3. 下列图形的主视图与左视图不相同的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，若AB=AC，则添加下列一个条件后，仍无法判定△ABE≌△ACD的是（）

A、 $∠ B = ∠ C$ B、BD=CE C、 $B E = C D$ D、∠AEB=∠ADC

查看试题解析
5. 如图， $▱ A B C D$ 的顶点B在y轴上，横坐标相等的顶点A、C分别在 $y = \frac{k_{1}}{x}$ 与 $y = \frac{k_{2}}{x}$ 图象上，则 $▱ A B C D$ 的面积为（　　）

A、 $\frac{1}{2} (k_{1} + k_{2})$ B、 $k_{1} + k_{2}$ C、 $\frac{1}{2} (k_{1} - k_{2})$ D、 $k_{1} - k_{2}$

查看试题解析
6. 由5个大小相同的正方形拼成如图所示的图形（阴影部分），在图中 $A$ ， $B$ ， $C$ ， $D$ 四个位置中再选择一个正方形，使新拼接成的图形折叠后成为一个封闭正方体的位置有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，已致点 $A_{1}$ 的坐标为 $(0 ， 1)$ ，点 $A_{2}$ 在 $x$ 轴的正半轴上，且 $∠ A_{1} A_{2} 0 = 30 °$ .过点 $A_{2}$ 作 $A_{2} A_{3} ⊥ A_{1} A_{2}$ ，交 $y$ 轴于点 $A_{3}$ ；过点 $A_{3}$ 作 $A_{3} A_{4} ⊥ A_{2} A_{3}$ ，交 $x$ 轴于点 $A_{4}$ ；过点 $A_{4}$ 作 $A_{4} A_{5} ⊥ A_{3} A_{4}$ ，交 $y$ 轴于点 $A_{5}$ ；……；按此规律进行下去，则点 $A_{2021}$ 的坐标为（）

A、 $(0 ， 3^{1011})$ B、 $(- 3^{1011} ， 0)$ C、 $(0 ， 3^{1010})$ D、 $(- 3^{1010} ， 0)$

查看试题解析
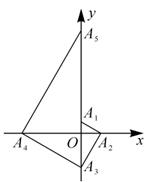8. 如图，点A、B为直线y＝x上的两点，过A、B两点分别作y轴的平行线交双曲线 $y = \frac{1}{x}$ （x＞0）于点C、D两点.若BD＝2AC，则4OC²﹣OD²的值为（）

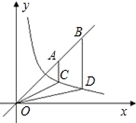A、5 B、6 C、7 D、8

查看试题解析
9. 如图是一根起点为1的数轴，现有同学将它弯折，弯折后虚线上第一行的数是1，第二行的数是13，第三行的数是43，…，依此规律，第五行的数是（）

A、183 B、157 C、133 D、91

查看试题解析
10. 如图，一次函数 $y = \frac{4}{3} x + 4$ 的图象与 $x$ 轴、 $y$ 轴分别相交于点 $A$ 、 $B$ ，点 $C$ 在反比例函数 $y = \frac{k}{x} (x < 0)$ 的图象上.若 $△ A B C$ 是等腰直角三角形，则下列 $k$ 的值错误的是（）

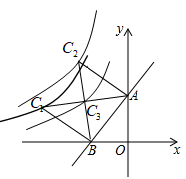A、-28 B、-21 C、-14 D、 $- \frac{49}{4}$

查看试题解析

二、填空题（共26分）

11. 若直角三角形的两直角边长为3、4，则该直角三角形的外接圆半径为．

查看试题解析
12. 若实数a满足 $\sqrt{2 a - 2}$ =4，则a的值为

查看试题解析
13. 如图，△ABC中，AB＝8cm，BC＝5cm，AC＝6cm，沿过点B的直线折叠三角形，使点C落在AB边上的点E处，折痕为BD ，则△AED的周长长度为．

查看试题解析
14. 已知三角形第一边的长为 $2 a + b$ ，第二边比第一边长a-b，第三边比第二边短a，则这个三角形的周长是（用含字母的代数式表示）

查看试题解析
15. 若点P（-5，a）与Q（b， $- \frac{1}{5}$ ）关于x轴对称，则代数式 $a^{2021} b^{2020}$ 的值为．

查看试题解析
16. 如图， $Δ A B C$ 中， $∠ A C B = 90 °$ ， $\sin A = \frac{5}{13}$ ， $A C = 12$ ，将 $Δ A B C$ 绕点 $C$ 顺时针旋转90º得到 $Δ A' B' C$ ， $P$ 为线段 $A' B'$ 上的动点，以点 $P$ 为圆心， $P A'$ 长为半径作⊙ $P$ ，当⊙ $P$ 与 $Δ A B C$ 的边相切时，⊙ $P$ 的半径为.

查看试题解析
17. 2019年9月，科学家将“42”写成了“ ${(- 80538738812075974)}^{3} + 80435758145817515^{3} +$ $12602123297335631^{3}$ ”的形式.至此，100以内的正整数（9ni4）型的数除外）都写成了三个整数的立方和的形式.试将下列整数写成三个非零且互不相等的整数的立方和的形式： $2 =$ ； $45 =$ .

查看试题解析
18. 如图（1），四边形ABCD和四边形AEFG都是正方形，将正方形AEFG绕点A旋转，连接BE、CF．

(1)、 $F C ： B E$ 的值为．

(2)、当G、F、C三点共线时，如图（2），若 $A B = 5$ 、 $A E = \sqrt{5}$ ，则 $B E =$ ．

查看试题解析

三、解答题（共10题，共64分）

19. 若（2a-1）²+|2a+b|=0，且|c-1|=2，求c·（a³-b）的值

查看试题解析
20. 先化简，再求值：

(1)、已知x＝2＋ $\sqrt{3}$ ，y＝2－ $\sqrt{3}$ ，求（x＋y）（x－y）＋y（x＋2y）－（x－y）²的值；

(2)、已知x＝ $\sqrt{3}$ ＋ $\sqrt{2}$ ，y＝ $\sqrt{3}$ － $\sqrt{2}$ ，求x³y－xy³的值．

查看试题解析
21. 如图，在 $R t Δ A B C$ 中， $∠ C ＝ 90 °$ ， $A C > B C$ ，利用尺规作图法在边 $A B$ 上求作一点 $D$ ，使 $C D$ 分 $∠ A B C$ 为两个等腰三角形.（保留作图痕迹，不写作法）

查看试题解析
22. 如图，在某小区内拐角处的一段道路上，有一儿童在C处玩耍，一辆汽车从被楼房遮挡的拐角另一侧的A处驶来，已知CM＝3m，CO＝5m，DO＝3m，∠AOD＝70°，汽车从A处前行多少米才能发现C处的儿童（结果保留整数）？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75；sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

查看试题解析
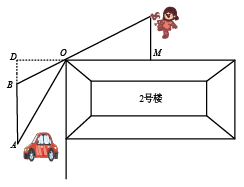23. 为弘扬中华民族传统文化，某市举办了中小学生“国学经典大赛”，比赛项目为：A．唐诗；B．宋词；C．论语；D．三字经．比赛形式分“单人组”和“双人组”．

(1)、小华参加“单人组”，他从中随机抽取一个比赛项目，恰好抽中“论语”的概率是多少？

(2)、小明和小红组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次．则恰好小明抽中“唐诗”且小红抽中“宋词”的概率是多少？小明和小红都没有抽到“三字经”的概率是多少？请用画树状图或列表的方法进行说明．

查看试题解析
24. 中学生带手机上学的现象越来越受到社会的关注，为此某记者随机调查了某区若干名中学生家长对这种现象的态度（态度分为：A.无所谓；B.基本赞成；C.赞成：D.反对）.并将调查结果绘制成折线统计图1和扇形统计图2（不完整）.请根据图中提供的信息，解答下列问题.

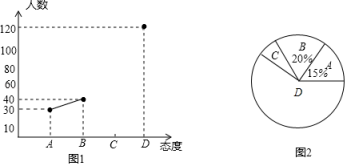(1)、此次抽样调查中，共调查了名中学生家长；

(2)、扇形统计图中，表示A类型的扇形圆心角的度数为.

(3)、先求出C类型的人数，然后将图1中的折线图补充完整.

(4)、根据抽样调查结果，请你估计该区18000名中学生家长中有多少名家长持反对态度？

查看试题解析
25. 如图，直线 $l_{1}$ 分别与x轴，y轴交于A､B两点，A､B的坐标分别为 $(2 ， 0)$ 、 $(0 ， 3)$ ，过点B的直线 $l_{2} ： y = \frac{1}{2} x + 3$ 交x轴于点C，点 $D (n ， 6)$ 是直线l上的一点，连接 $C D$ ．

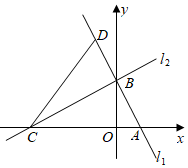(1)、求 $l_{1}$ 的解析式；

(2)、求C､D的坐标；

(3)、求 $△ B C D$ 的面积．

查看试题解析
26. 阅读下列材料，并回答问题，事实上，在任何一个直角三角形中，两条直角边的平方之和一定等于斜边的平方，这个结论就是著名的勾股定理．请利用这个结论，完成下面活动：

(1)、一个直角三角形的两条直角边分别为6、8，那么这个直角三角形斜边长为．

(2)、如图， $A D ⊥ B C$ 于 $D$ ， $A D = B D$ ， $A C = B E$ ， $A C = 3$ ， $D C = 1$ ，求 $B D$ 的长度．

(3)、如图，点 $A$ 在数轴上表示的数是多少？请用类似的方法在图数轴上画出表示数 $\sqrt{10}$ 的 $B$ 点（保留作图痕迹）

查看试题解析
27. 如图，已知抛物线y＝﹣x²+bx+c经过A（﹣1，0），B（3，0）两点.

(1)、求抛物线的解析式和顶点坐标；

(2)、当0＜x＜3时，直接写出y的取值范围；

(3)、点P为抛物线上一点，若S_△PAB＝10，求出此时点P的坐标.

查看试题解析
28. 在等腰梯形ABCD中，DC//AB，AB= 6， $t a n B = 2 \sqrt{2}$ ，过点A作AH⊥BC，垂足为点H．

(1)、当点C与点H重合时（如图），求线段BC的长；

(2)、当点C不与点H重合时，联结AC，作△ACH的外接圆O．
①当点C在BH的延长线上时（如图），设CH=x，CD = y，求y与x的函数解析式，并写出定义域；
②延长CD交圆O于点G，如果△ACH与△ACG全等，求CD的长

查看试题解析