浙江省绍兴市嵊州市四校联考2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-05-13 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每题2分，共20分）

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{1.5}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{2}$

查看试题解析
3. 下列方程是一元二次方程的是 $($ $)$

A、 $- 6 x + 2 = 0$ B、 $2 x^{2} - y + 1 = 0$ C、 $x^{2} + 2 x = 0$ D、 $\frac{1}{x^{2}} + x = 2$

查看试题解析
4. 正十二边形的外角和的度数为（）

A、 $180^{\circ}$ B、 $360^{\circ}$ C、 $720^{\circ}$ D、 $1800^{\circ}$

查看试题解析
5. 某班10名学生体育测试的成绩分别为（单位：分）58，60，59，52，58，55，57，58，49，57（体育测试这次规定满分为60分），这组数据的众数是（）

A、58 B、57 C、59 D、55

查看试题解析
6. 一元二次方程 $x^{2} + 5 x - 3 = 0$ 根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
7. 如图，在四边形 $A B C D$ 中， $A B / / C D$ ，要使四边形 $A B C D$ 是平行四边形，下列添加的条件不正确的是（）

A、 $A D = B C$ B、 $A B = C D$ C、 $A D / / B C$ D、 $∠ A = ∠ C$

查看试题解析
8. 如图，在△ABC中，点D，E分别是边AB，BC的中点，若△DBE的周长是7，则△ABC的周长是（）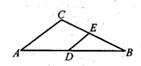

A、8 B、10 C、12． D、14

查看试题解析
9. 如图，在 $▱ A B C D$ 中， $∠ A = 70^{\circ}$ ，将 $▱ A B C D$ 折叠，使点D，C分别落在点F，E处（点F，E都在 $A B$ 所在的直线上），折痕为 $M N$ ，则 $∠ A M F$ 等于（）

A、 $70^{\circ}$ B、 $40^{\circ}$ C、 $30^{\circ}$ D、 $20^{\circ}$

查看试题解析
10. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 交于点O， $A E$ 平分 $∠ B A D$ ，交 $B C$ 于点E，且 $∠ A D C = 60^{\circ}$ ， $A B = \frac{1}{2} B C$ ，连接 $O E$ ，下列结论：① $∠ C A D = 30^{\circ}$ ；② $O D = A B$ ；③ $S ▱ A B C D = A C \cdot C D$ ；④ $S_{四边形 O E C D} = \frac{3}{2} S_{Δ A O D}$ ，其中成立的个数为（）

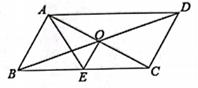A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共有8小题，每小题3分，共24分）

11. 计算 $\sqrt{{(- 3)}^{2}}$ 的结果是.

查看试题解析
12. 一组数据的方差为4，则标准差是．

查看试题解析
13. 某种产品原来售价为200元，经过连续两次大幅度降价处理，现按72元的售价销售．设平均每次降价的百分率为x，列出方程：．

查看试题解析
14. 在平面直角坐标系xOy中，若点B与点A(－2,3) 关于点O中心对称，则点B 的坐标为.

查看试题解析
15. 如果数据 $x_{1}$ ， $x_{2}$ 的平均数是80，那么 $x_{1} - 3$ ， $x_{2} - 3$ 的平均数

查看试题解析
16. 若m是方程 $2 x^{2} - 3 x - 1 = 0$ 的一个根，则 $4 m^{2} - 6 m$ 的值为．

查看试题解析
17. 已知方程 ${(x^{2} + y^{2})}^{2} - 2 (x^{2} + y^{2}) - 3 = 0$ ，则 $x^{2} + y^{2}$ 的值为．

查看试题解析
18. 如图，在四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点E． $∠ C B D = 90$ 度， $B C = 4$ ， $A C = 10$ ，则四边形 $A B C D$ 的面积为．

查看试题解析

三、解答题（本大题共有7小题，共56分）

19. 计算

(1)、 $(\sqrt{3} - 1) \times (\sqrt{3} + 1)$

(2)、 $\sqrt{8} + \sqrt{32} - \sqrt{2}$

查看试题解析
20. 解下列方程

(1)、 $x^{2} - 2 x = 0$

(2)、 $x^{2} - 6 x + 9 = 0$

查看试题解析
21. 已知关于x的方程 $x^{2} + m x - 6 = 0$ 的一个根为2，求m的值和方程的另一根．

查看试题解析

22. 甲、乙两名队员参加射击训练，每人射击10次，成绩分别如下：

根据以上信息，整理分析数据如下：

	平均成绩/环	中位数/环	众数/环
甲	a	7	7
乙	7	b	c

(1)、

a =

；

b =

；

c =

；

(2)、填空：（填“甲”或“乙”）．

①从平均数和中位数的角度来比较，成绩较好的是；

②从平均数和众数的角度来比较，成绩较好的是；

查看试题解析

23. 如图，四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，点E，F分别在线段 $O A$ ， $O C$ 上，且 $O B = O D$ ． $∠ 1 = ∠ 2$ ， $A E = C F$ .

(1)、证明： $Δ B E O ≅ Δ D F O$ ；

(2)、证明：四边形 $A B C D$ 是平行四边形．

查看试题解析
24. 某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为了扩大销售减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫降价1元，商场平均每天可多售出2件．若设每件衬衫降价x元，解答下列问题：

(1)、当每件衬衫降价5元，则每件利润元，平均每天可售出件．

(2)、若平均每天获利为y元，请求出y与x的函数关系式.

(3)、若商场想平均每天盈利1200元，每件衬衫应降价多少元？

查看试题解析
25. 如图所示，在 $△ A B C$ 中， $∠ C = 90^{\circ}$ ， $A C = 6 cm$ ， $B C = 8 cm$ ，点P从点A出发沿边 $A C$ 向点C以 $1 cm/s$ 的速度移动，点Q从C点出发沿 $C B$ 边向点B以 $2 cm/s$ 的速度移动．

(1)、如果P、Q同时出发，几秒钟后，可使 $△ P C Q$ 的面积为8平方厘米？

(2)、点P、Q在移动过程中，是否存在某一时刻，使得 $△ P C Q$ 的面积等于 $△ A B C$ 的面积的一半．若存在，求出运动的时间；若不存在，说明理由.

查看试题解析