浙江省杭州市萧山区城区2021-2022学年八年级下学期期中数学试卷

试卷更新日期：2022-05-13 类型：期中考试

进入出卷网下载

一、单选题（每小题3分，共30分）

1. 要使二次根式 $\sqrt{x + 3}$ 有意义，则x的取值范围是（）

A、x≠﹣3 B、x≤﹣3 C、x＞﹣3 D、x≥﹣3

查看试题解析
2. 如图所示车标中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 用配方法解方程x²﹣x﹣1＝0时，配方结果正确的是（）

A、（x﹣1）²＝2 B、（x $- \frac{1}{2}$ ）² $= \frac{5}{4}$ C、（x $- \frac{1}{2}$ ）²＝1 D、（x $- \frac{1}{2}$ ）² $= \frac{3}{4}$

查看试题解析
4. 八年级一班七个兴趣小组人数分别为4，4，5，x，6，6，7，已知这组数据的平均数是5，则这组数据的中位数是（）

A、7 B、6 C、5 D、4

查看试题解析
5. 下列计算正确的是（）

A、 $\frac{\sqrt{27} - \sqrt{12}}{3} = \sqrt{9} - \sqrt{4} =$ 1 B、 $\frac{6 - \sqrt{2}}{\sqrt{2}} =$ 3 $\sqrt{2}$ C、（2 $+ \sqrt{5}$ ）（2 $- \sqrt{5}$ ）＝1 D、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$

查看试题解析
6. 下列条件不能判定四边形是平行四边形的是（）
①一组对边平行，另一组对边相等的四边形是平行四边形；②一组对角相等，一组邻角互补的四边形是平行四边形；③对角线相等且互相垂直的四边形是平行四边形；④一组对边平行，一组对角相等的四边形是平行四边形；

A、①③ B、②④ C、①④ D、以上都不正确

查看试题解析
7. 新冠疫情牵动人心，若有一人感染了新冠，设每轮传染中平均一个人传染了x个人，经过两轮传染后共有400人感染，列出的方程是（）

A、1+x+x²＝400 B、1+2x＝400 C、x+x（1+x）＝400 D、（1+x）²＝400

查看试题解析
8. 在△ABC中，三边分别为a，b，c，则化简|a﹣b+c|﹣2 $\sqrt{{(c - a - b)}^{2}}$ 的结果为（）

A、3a+b﹣c B、﹣a﹣3b+3c C、a+3b﹣3c D、2a

查看试题解析
9. 已知关于x的方程mx²+x﹣m+1＝0，给出以下结论，其中错误的是（）

A、当m＝0时，方程只有一个实数根 B、若x $= \frac{3}{4}$ 是方程的根，则方程的另一根为x＝﹣1 C、无论m取何值，方程都有一个负数根 D、当m≠0时，方程有两个不相等的实数根

查看试题解析
10. 如图，四边形ABCD中，AB∥CD，∠B＝∠D，点E为BC延长线上一点，连接AE，AE交CD于点H，∠DCE的平分线交AE于点G．若AB＝2AD＝10，点H为CD的中点，HE＝6，则AC的值为（）

A、9 B、 $\sqrt{97}$ C、10 D、3 $\sqrt{10}$

查看试题解析

二、填空题（每小题4分，共24分）

11.

(1)、 $\sqrt{2} \times \sqrt{6} =$ ；

(2)、 $\frac{\sqrt{24}}{\sqrt{3}} =$ ．

查看试题解析
12. 若一组数据1，2，x，4的众数是1，则这组数据的方差为．

查看试题解析
13. 设实数 $\sqrt{10}$ 的整数部分为a，小数部分为b，则（2a+b）（2a﹣b）＝．

查看试题解析
14. 已知多边形的内角和等于外角和的两倍，则这个多边形是边形．

查看试题解析
15. 如图，在平行四边形ABCD中，E为BC边上一点，且AB＝AE．若AE平分∠DAB，∠EAC＝10°，则∠AED＝．

查看试题解析
16. 对于一元二次方程ax²+bx+c＝0（a≠0），下列说法正确的有．
①若b＝2 $\sqrt{a c}$ ，则此方程一定有两个相等的实数根；

②若此方程有两个不等的实数根，则方程x²﹣bx+ac＝0也一定有两个不等的实数根；

③若a﹣b+c＝0，则此方程一定有两个不等的实数根；

④若x₀是一元二次方程ax²+bx+c＝0的根，则b²﹣4ac＝（2ax₀+b）²；

查看试题解析

三、解答题（共66分）

17. 计算：

(1)、2 $\sqrt{20} - \sqrt{5} +$ 3 $\sqrt{\frac{1}{5}}$ ；

(2)、（ $\sqrt{x - 3}$ ）² $- \sqrt{4 - 4 x + x^{2}}$ ．

查看试题解析
18. 用适当的方法解下列方程：

(1)、x²﹣x﹣6＝0；

(2)、4（x﹣1）²＝9（x﹣5）² ．

查看试题解析
19. 某工艺品厂草编车间共有16名工人，调查每个工人的日均生产能力，获得数据如下表：

日均生产能力（件）

10

11

12

13

14

15

人数

1

3

5

4

2

1

(1)、求这16名工人日均生产件数的平均数、众数、中位数．

(2)、若以中位数作日生产件数的定额，求能完成任务的工人数占总人数的比值？

查看试题解析
20. 一商店销售某种商品，平均每天可售出20件，每件盈利40元，为了扩大销售，增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间的销售，发现销售单价每降低1元，平均每天可多售出2件．

(1)、若降价a元，则平均每天的销售数量为件（用含a的代数式表示）．

(2)、当每件商品降价多少元时，该商店每天的销售利润为1200元？

(3)、该商店每天的销售利润可能达到1450元吗？请说明理由．

查看试题解析
21. 在四边形ABCD中，AC、BD交于点O，AD∥BC，AO＝CO．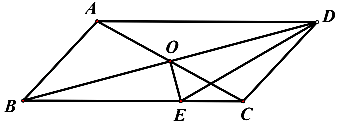

(1)、证明：四边形ABCD是平行四边形；

(2)、过点O作OE⊥BD交BC于点E，连接DE．若∠CDE＝∠CBD＝15°，求∠ABC的度数．

查看试题解析
22. 先阅读下面的例题，再按要求解答下列问题：
求代数式y²+4y+8的最小值．

解：y²+4y+8＝y²+4y+4+4＝（y+2）²+4，

∵（y+2）²≥0，

∴（y+2）²+4≥4

∴y²+4y+8的最小值是4．

(1)、求代数式m²+m+4的最小值；

(2)、求代数式24﹣2x²+8x的最大值；

(3)、某居民小区要在一块靠墙（墙长15m）的空地上建一个长方形花园ABCD，花园一边靠墙，另三边用总长为20m的栅栏围成．如图，设AB＝x（m），请问：当x取何值时，花园的面积最大？最大面积是多少？

查看试题解析
23. 如图，在长方形ABCD中，BC＝20cm，P、Q、M、N分别从A、B、C、D出发沿AD、BC、CB、DA方向在长方形的边上同时运动，当有一个点先到达所在运动边的另一个端点时即停止，已知在相同时间内，若BQ＝xcm（x≠0），则AP＝2xcm，CM＝3xcm，DN＝x²cm．

(1)、当x为何值时，点的运动停止？

(2)、点P与点N可能相遇吗？点Q与点M呢？请通过计算说明理由．

(3)、当x为何值时，以P、Q、M、N为顶点的四边形是平行四边形？

查看试题解析

日均生产能力（件）	10	11	12	13	14	15
人数	1	3	5	4	2	1