浙江省舟山市定海区2022年初中毕业升学考试调研测试（一模）数学试卷

试卷更新日期：2022-05-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 有理数3，1，﹣2，4中，小于0的数是（）

A、3 B、1 C、﹣2 D、4

查看试题解析
2. 人口普查得知，舟山市常住人口约为116万人，用科学记数法表示为（）

A、1.16×10²人 B、1.16×10⁶人 C、11.6×10⁵人 D、116×10⁴人

查看试题解析
3. 如图是由4个小正方形体组合成的几何体，该几何体的主视图是（）

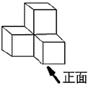A、 B、 C、 D、

查看试题解析
4. 如图，有5张形状、大小、材质均相同的卡片，正面分别印着北京2022年冬奥会的越野滑雪、速度滑冰、花样滑冰、高山滑雪、单板滑雪大跳台的体育图标，背面完全相同．现将这5张卡片洗匀并正面向下放在桌上，从中随机抽取一张，抽出的卡片正面恰好是“滑冰”项目的图案的可能性是（）．

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 下列运算正确的是（）

A、 $\frac{1}{x} + \frac{1}{y} = \frac{1}{x + y}$ B、 ${(- p^{2} q)}^{3} = - p^{5} q^{3}$ C、 $\sqrt{a} \cdot \sqrt{b} = \sqrt{a b}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
6. 如图，已知a $∥$ b，含30°角的直角三角板的顶点在直线b上，若∠1＝26°，则∠2等于（）

A、90° B、112° C、114° D、116°

查看试题解析
7. 初三体育素质测试，某小组5名同学成绩如下表所示，有两个数据被遮盖，如下表：
编号
1
2
3
4
5
方差
平均成绩
得分
38
34
37
40
37
那么被遮盖的两个数据依次是（）

A、35，2 B、36，4 C、35，3 D、36，5

查看试题解析
8. 直线 $y = x - a$ 不经过第二象限，且关于x的方程 $a x^{2} - 2 x + 1 = 0$ 有实数解，则a的取值范围是（）

A、0≤a≤1 B、0≤a<1 C、0<a≤1 D、0<a<1

查看试题解析
9. 如图所示，等腰 $R t △ A B C$ 与等腰 $R t △ D A E$ 中， $∠ B A C = ∠ D A E = 90 °$ ， $A B = A C = 2$ ， $A D = A E = 1$ ，则 $B D^{2} + C E^{2} =$ （）

A、9 B、11 C、10 D、12

查看试题解析
10. 现有函数 $y = {\begin{array}{l} x - 4 (x \geq a) \\ - x^{2} - 2 x (x < a) \end{array}$ 如果对于任意的实数n，若直线y＝n与函数 $y = {\begin{array}{l} x - 4 (x \geq a) \\ - x^{2} - 2 x (x < a) \end{array}$ 的图象总有交点，那么实数a的取值范围是（）

A、 $- 5 \leq a \leq 4$ B、 $- 1 \leq a \leq 4$ C、 $- 4 \leq a \leq 1$ D、 $- 4 \leq a \leq 5$

查看试题解析

二、填空题

11. 分解因式： $x^{2} - 5 x$ = ．

查看试题解析
12. 如图，在⊙O中，点C为优弧ACB上的一点， $\overset{⌢}{A B} = 168 °$ ，则∠C=.

查看试题解析
13. 如图，在直角坐标系中， $△$ OAB的顶点为O（0，0），A（4，3），B（3，0）.以点O为位似中心，在第三象限内作与 $△$ OAB的位似比为 $\frac{1}{3}$ 的位似图形 $△$ OCD，则点C的坐标为 .

查看试题解析
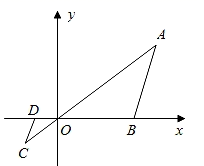
14. 《九章算术》是我国古代数学名著，卷七“盈不足”中有题译文如下：今有人合伙买一只羊，每人出5钱，会差45钱；每人出7钱，会差3钱.问合伙人数、羊价各是多少？设羊价为x钱，所列方程是.

查看试题解析
15. 如图是4个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作 $T_{m}$ （ $m$ 为1~4的整数），函数 $y = \frac{k}{x}$ （ $x > 0$ ）的图象为曲线 $L$ .若曲线 $L$ 使得 $T_{1} ~ T_{4}$ ，这些点分布在它的两侧，每侧各2个点，则 $k$ 的取值范围是.

查看试题解析
16. 点G为ΔABC的重心（三角形三条中线的交点），BC＝12，∠A＝60°.

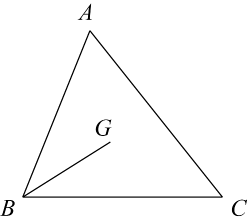(1)、若∠C＝30°，则BG＝.

(2)、BG的最大值为.

查看试题解析

三、解答题

17.

(1)、计算：(1- $\sqrt{2}$ )⁰+2cos45°- $\sqrt{8}$

(2)、化简： $（ a + 2 ）^{2} - a (a - 1)$

查看试题解析
18. 阅读下列解题过程.
解方程：
$\frac{1}{x + 2} + \frac{4 x}{(x + 2) (x - 2)} = \frac{2}{2 - x}$
解：方程两边同乘以 $(x + 2) (x - 2)$ ，
得 $(x + 2) (x - 2) [\frac{1}{x + 2} + \frac{4 x}{(x + 2) (x - 2)}] = \frac{2}{2 - x} (x + 2) (x - 2)$
方程两边化简，得 $(x - 2) + 4 x = 2 (x + 2)$
去括号，移项，得 $x - 2 + 4 x - 2 x - 4 = 0$
解这个方程，得 $x ＝ 2$ .
你认为此解法是否正确？若不正确，请写正确的解题过程

查看试题解析
19. 上海某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，那么当成人按规定剂量服用后，根据图象回答下列问题.

(1)、服药后几小时，血液中含量最高；最高每毫升多少微克？

(2)、当2≤x≤8时，y关于x的函数解析式；

(3)、如果每毫升血液中含药量为3微克或3微克以上时治疗疾病最有效，那么这个新药的有效时长是多少小时？

查看试题解析
20. 如图，∠PAQ是直角，半径为5的圆O经过AP上的点T，与AQ相交于点B，C两点，且TB平分∠OBA.

(1)、求证：AP是⊙O的切线；

(2)、已知AT＝4，试求BC的长.

查看试题解析
21. 农民也可以报销医疗费了！”这是我区推行新型农村合作医疗的成果.村民只要每人每年交100元钱，就可以加入合作医疗，大病先由自己支付医疗费，年终时可得到按一定比例的返回款，这一举措大大增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民，根据收集到的数据绘制了以下的统计图.根据信息，解答以下问题：

(1)、本次调查了多少村民？被调查的村民中，有多少参加合作医疗得到了返回款？

(2)、该乡若有10000村民，请你估计有多少人参加了合作医疗？要使两年后参加合作医疗的人数增加到9680人，假设这两年的年增长率相同，求这个年增长率.

(3)、参加合作医疗遭遇重大疾病的村民得到的返回款人均5000元，从总体回报的角度看，是否建议参加新型农村合作医疗？说明理由.

查看试题解析
22. 为了监控危险路段的车辆行驶情况，通常会设置电子眼进行区间测速.如图电子眼位于点P处，离地面的铅垂高度PQ为11米；离坡AB的最短距离是11.2米，坡AB的坡比为3：4；电子眼照射在A 处时，电子眼的俯角为30°，电子眼照射在坡角点B处时，电子眼的俯角为70°.（A、B、P、Q在同一平面内）

(1)、求路段BQ的长；（sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

(2)、求路段AB的长；（ $\sqrt{3}$ ≈1.7，结果保留整数）

(3)、如图的这辆车看成矩形KLNM，车高2米，当PA过M点时开始测速，PB过M点时结束测速，若在这个测速路段车辆所用的时间是1.5秒.该路段限速5米/秒，计算说明该车是否超速？

查看试题解析
23. 某城市发生疫情，第x天（1≤x≤12）新增病例y（人）如下表所示：
x
1
2
3
4
……
11
12
y
1
16
33
53
……
241
276

(1)、疫情前12天的人数模型基本符合二次函数 $y = a x^{2} + b x - 12$ ，根据图表，求出二次函数解析式；

(2)、由于政府进行管控，第12天开始新增病例逐渐下降，第x天（x>12）新增病例y（人）近似满足 $y = 4 (x - a) (x - 35)$ .请预计第几天新增病例清零；

(3)、为应对本轮疫情，按照每一确诊病例需提供一张病床的要求，政府准备了2100张病床.你认为病床够了吗？请说明理由.

查看试题解析
24. 如图1，在矩形ABCD中，P是BC上的点，ΔABP沿AP折叠B点的对应点是M点，延长PM交直线AD于点E.

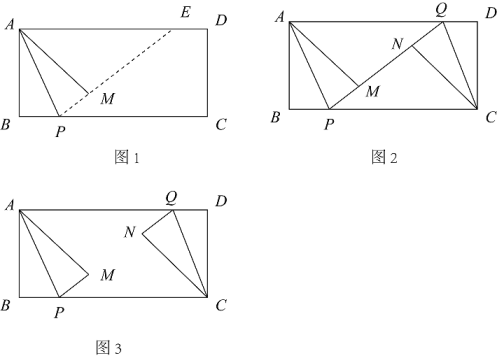(1)、求证：EA＝EP

(2)、如图2，Q是AD上的点，QD＝BP；ΔCDQ沿CQ折叠D点的对应点是N点，且P、M、N、Q在同一直线上.
①若AB＝4，AD＝8；求BP的长.

②若M、N互相重合；求 $\frac{A B}{A D}$ 的值；（自己画草图）

(3)、如图3，Q是AD上的点，QD＝BP；ΔCDQ沿CQ折叠D点的对应点是N点，若AB＝4，MN的最小值是1；求AD的长.

查看试题解析

编号	1	2	3	4	5	方差	平均成绩
得分	38	34		37	40		37

x	1	2	3	4	……	11	12
y	1	16	33	53	……	241	276