浙江省温州市文成县2022年初中学业水平适应性考试（一模）数学试卷

试卷更新日期：2022-05-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 数 $\sqrt{2}$ ，－2，0，3中为无理数的是（）

A、 $\sqrt{2}$ B、－2 C、0 D、3

查看试题解析
2. 第24届冬奥会于2022年月2月4日在北京开幕，吉样物冰墩墩因其憨态可掬的造型迅速火遍全球.某移动公司购进10086个冰墩墩奖励新办移动宽带的客户，10086用科学记数法表示为（）

A、 $10.086 \times 1 0^{3}$ B、 $0.10086 \times 1 0^{5}$ C、 $1.0086 \times 1 0^{3}$ D、 $1.0086 \times 1 0^{4}$

查看试题解析
3.
一个几何体的三视图如下图所示，这个几何体是（）

A、球 B、圆柱 C、长方体 D、圆锥

查看试题解析
4. 下列计算正确的是（）

A、 ${(m + 1)}^{2} = m^{2} + 1$ B、 $y^{6} \div y^{2} = y^{3}$ C、 ${(- 2 m)}^{3} = - 6 m^{3}$ D、 $y^{3} \cdot y^{2} = y^{5}$

查看试题解析
5. 九（1）班5名同学平均每周课外阅读时间分别为6，5，7，5，8小时，则他们平均每周课外阅读时间的中位数是（）

A、5时 B、6时 C、7时 D、8时

查看试题解析
6. 如图 $▱ A B C D$ 中，AB＝4，BD＝6， $B D ⊥ A B$ ，则AC的长为（）

A、10 B、2 $\sqrt{13}$ C、5 D、2 $\sqrt{5}$

查看试题解析
7. 如图，小羽利用仪器测量一电线杆AB的拉线AC的长度，测得拉线AC与水平地面BC的夹角为 $7 0^{∘}$ ，并测得C点到电线杆的距离BC为5米，则拉线AC的长度为（）

A、 $\frac{5}{s i n 7 0^{∘}}$ 米 B、 $\frac{5}{c o s 7 0^{∘}}$ 米 C、 $5 s i n 7 0^{∘}$ 米 D、 $5 c o 67 0^{∘}$ 米

查看试题解析
8. 我国古代数学名著《孙子算经》中记载了一道题，大意是：求100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（　　）

A、 $\{\begin{matrix} x + y = 100 \\ 3 x + 3 y = 100 \end{matrix}$ B、 $\{\begin{matrix} x + y = 100 \\ x + 3 y = 100 \end{matrix}$ C、 $\{\begin{matrix} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{matrix}$ D、 $\{\begin{matrix} x + y = 100 \\ 3 x + y = 100 \end{matrix}$

查看试题解析
9. 已知 $(x_{1} ， y_{1}) ， (x_{2} ， y_{2})$ 是抛物线 $y = x^{2} - 2 x + m$ 上的点，若 $- 3 < x_{1} \leq - 2$ ， $3 < x_{2} \leq 4$ ，则（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} \geq y_{2}$ D、 $y_{1} \leq y_{2}$

查看试题解析
10. 如图，图中小正方形的组合图形是棱长为1的正方体一种表面展开图，过小正方形的顶点A，B，C，D的线段AB，CD与经过小正方形的顶点E，F的直线交于点M，N，则线段MN的长为（）

A、2 $\sqrt{2}$ B、 $1 + \sqrt{2}$ C、 $\frac{5}{2}$ D、 $\frac{7}{4}$ $\sqrt{2}$

查看试题解析

二、填空题

11. 因式分解： $a^{2} - 4$ =.

查看试题解析
12. 不等式组 ${\begin{array}{l} x - 1 < 4 \\ \frac{x + 1}{2} \geq 1 \end{array}$ 的解集为.

查看试题解析
13. 冬奥会冰上项目有短道速滑、速度滑冰、花样滑冰、冰球、冰壶5个.其中短道速滑、速度滑冰、花样滑冰为滑冰大项里的3个分项.小华去冰上项目当志愿者，则他被随机分派到滑冰大项里当志愿者的概率为.

查看试题解析
14. 如图，点A，B，C都在⊙O上， $∠ A O C ： ∠ B O C = 2 ： 5$ ， $O A / / B C$ ，则∠ABC＝°.

查看试题解析
15. 若A（a，a+5），B（b，b-5）是反比例图象上的两点，则线段AB的长为.

查看试题解析
16. 如图1，点E，F是矩形纸片ABCD的边AD上两点，将△ABE和△DCF分别沿BE和CF翻折后（如图2），四边形EDAF恰为矩形，其中 $E F ： B C = 2 ： 7$ ，如果梯形EBCF的面积比矩形ABCD的面积小300cm² ，则折纸后三层重叠部分即四边形M $D$ N $A$ 的面积为cm².

查看试题解析

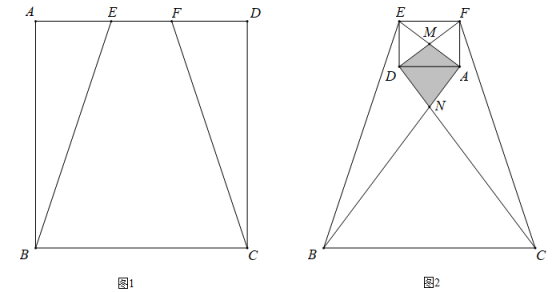
三、解答题

17.

(1)、计算： $| - 3 | - \sqrt{16} + {(\sqrt{3} - 1)}^{0} + {(- 2)}^{2}$

(2)、化简： ${(m + 2)}^{2} + m (m - 4)$

查看试题解析
18. 如图，AC，BD交于点O， $O A = O B$ ， $∠ C = ∠ D$ .

(1)、求证： $Δ A B C ≅ Δ B A D$ ；

(2)、若 $A B = A C$ ， $∠ A B D = 3 0^{∘}$ ，求∠C的度数.

查看试题解析
19. 某校想了解学生每天的运动情况，随机调查了部分学生，对学生每天的运动时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数直方图和扇形统计图：

(1)、求此次调查的总人数并补全频数直方图.

(2)、为了响应“每天运动一小时”的口号，学校提出每天运动时间达到0.5小时且小于1.5小时的学生可评为“运动达人”.若该校共有480名学生，请你估计该校有多少名学生可获得“运动达人”的称号.

查看试题解析
20. 如图，在6×6的方格中，有一格点△ABC（顶点都在小正方形的顶点上）及格点P，按下列要求画格点三角形.

(1)、在图1中，画出△ABC绕点P顺时针旋转90°后的三角形△A′B′C′.

(2)、在图2中，画出△ABC绕某一点顺时针旋转90°后的△DEF，且点P在△DEF内（不包括边界）

查看试题解析
21. 已知抛物线 $y = - x^{2} + b x + c$ 与x轴的一个交点为（－1，0），且经过点（2，c）.

(1)、求抛物线与x轴的另一个交点坐标.

(2)、当 $t \leq x \leq 2 - t$ 时，函数的最大值为M，最小值为N，若 $M - N = 3$ ，求t的值.

查看试题解析
22. 如图，在四边形ABCD中， $D A = D C$ ， $∠ A D C = ∠ B = 9 0^{∘}$ ，过点D作 $D E ⊥ A B$ 于E.

(1)、求证： $D E = B E$ .

(2)、连结AC交DE于点F，若 $t a n ∠ A D E = \frac{1}{2}$ ， $A D = 15$ ，求DF的长.

查看试题解析
23. “互联网＋”让我国经济更具活力，直播助销就是运用“互联网＋”的生机勃勃的销售方式，让大山深处的农产品远销全国各地.小聪为当地甲、乙、丙三种特色产品助销.已知每包甲的售价比每包乙的售价低40元，某顾客购买数量相同的甲产品和乙产品分别花了200元和1000元.

(1)、求每包甲、乙产品的售价.

(2)、已知甲产品的成本为8元/包，乙产品的成本为36元/包，小聪计划助销100包，总成本1500元.
①若只助销甲、乙两种产品，则可获利多少元？
②若助销三种产品，丙产品成本为6元/包，售价为9元/包，则最多可获利多少元？

查看试题解析
24. 如图，已知：在△ABC中， $∠ C = 9 0^{∘}$ ，点P是BC边上的动点. $P D ⊥ B C$ 交AB于D.以PD为直径的⊙O分别交AB，AP于点E，F.

(1)、求证： $∠ E F P = ∠ E P B$ .

(2)、若 $A B = 20$ ， $s i n B = \frac{3}{5}$ .
①当 $∠ A P B = 4 ∠ A P D$ ，求PC的长.

②当△PEF为等腰三角形时，请求出所有满足条件的△PEF的腰长.

(3)、若 $s i n B = \frac{\sqrt{2}}{2}$ ，且D，F，C在一条直线上，则DP与AC的比值为.

查看试题解析