浙江省台州市临海市2022年中考数学一模试卷
试卷更新日期:2022-05-13 类型:中考模拟
一、单选题
-
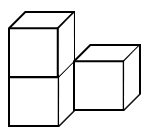
1. 计算1﹣2的结果是( )A、﹣1 B、1 C、﹣3 D、32. 如图是由立方体叠成的立体图形,从正面看,得到的主视图为( )
 A、
A、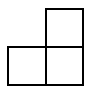 B、
B、 C、
C、 D、
D、 3. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
3. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列整式运算中正确的是( )A、 B、 C、 D、5. 与的值最接近的整数是( )A、2 B、3 C、4 D、56. 如图,已知点A,B的坐标分别为 , , 四边形是平行四边形,点C的坐标为 , 则点D的坐标为( )
4. 下列整式运算中正确的是( )A、 B、 C、 D、5. 与的值最接近的整数是( )A、2 B、3 C、4 D、56. 如图,已知点A,B的坐标分别为 , , 四边形是平行四边形,点C的坐标为 , 则点D的坐标为( ) A、 B、 C、 D、7. 2021年,党中央国务院赋予浙江省建设“共同富裕示范区”的光荣使命,共同富裕的要求是:在消除两极分化和贫穷基础上实现普遍富裕.下列有关人均收入的统计量特征中,最能体现共同富裕要求的是( )A、方差小 B、平均数小,方差小 C、平均数大,方差小 D、平均数大,方差大8. 已知 , 则下列结论中一定正确的是( )A、 B、 C、 D、9. 如图,有一张菱形纸片 , 分别把沿着两条平行于的直线进行对折,得到一个六边形 , 如果这个六边形是正六边形,则菱形的对角线长的比( )
A、 B、 C、 D、7. 2021年,党中央国务院赋予浙江省建设“共同富裕示范区”的光荣使命,共同富裕的要求是:在消除两极分化和贫穷基础上实现普遍富裕.下列有关人均收入的统计量特征中,最能体现共同富裕要求的是( )A、方差小 B、平均数小,方差小 C、平均数大,方差小 D、平均数大,方差大8. 已知 , 则下列结论中一定正确的是( )A、 B、 C、 D、9. 如图,有一张菱形纸片 , 分别把沿着两条平行于的直线进行对折,得到一个六边形 , 如果这个六边形是正六边形,则菱形的对角线长的比( ) A、 B、 C、 D、10. 三个方程的正根分别记为 , 则下列判断正确的是( )A、 B、 C、 D、
A、 B、 C、 D、10. 三个方程的正根分别记为 , 则下列判断正确的是( )A、 B、 C、 D、二、填空题
-
11. 因式分解: =.12. 把一枚均匀的硬币连续抛掷两次,两次正面朝上的概率是 .13. 根据光学中平面镜光线反射原理,入射光线、反射光线与平面镜所夹的角相等.如图,是两面互相平行的平面镜,一束光线m通过镜面反射后的光线为n,再通过镜面β反射后的光线为k.光线m与镜面的夹角的度数为 , 光线n与光线k的夹角的度数为.则x与y之间的数量关系是.
 14. 如图,在中,点D,E分别是的中点,与相交于点F.若 , 则的长是.
14. 如图,在中,点D,E分别是的中点,与相交于点F.若 , 则的长是. 15. 如图是函数和函数在第一象限部分的图象,则时,使成立的x的取值范围是.
15. 如图是函数和函数在第一象限部分的图象,则时,使成立的x的取值范围是. 16. 如图,矩形纸条中, , 把该纸条依次沿着互相平行的两条直线对折得到“Z”字形图案.已知 , 要使点H,点K分别在和的延长线上(不与D,F重合),则;的取值范围是.
16. 如图,矩形纸条中, , 把该纸条依次沿着互相平行的两条直线对折得到“Z”字形图案.已知 , 要使点H,点K分别在和的延长线上(不与D,F重合),则;的取值范围是.
三、解答题
-
17. 计算:(1)、;(2)、.18. 解二元一次方程组19. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表:
镜片焦距(米)
1.00
0.50
0.25
0.20
0.10
近视眼镜的度数(度)
100
200
400
500
1000
(1)、请写出适当的函数解析式描述近视眼镜的度数y与镜片焦距x的关系;(2)、验光师测得小明同学的近视度数是250度,给小明配的眼镜的焦距应该是多少米?20. 如图,为了建设一条贯穿山峰的东西方向隧道 , 在规划中首先需要测量A,B之间的距离.无人机保持离水平道路的竖直高度,从点A的正上方点C出发,沿正东方向飞行到达点D,测得点B的俯角为.求的长度.(参考数据:) 21. 如图,半圆O的直径 , 圆心为点O.点E在上,四边形是平行四边形,顶点C在半圆上, , 垂足为F,.
21. 如图,半圆O的直径 , 圆心为点O.点E在上,四边形是平行四边形,顶点C在半圆上, , 垂足为F,. (1)、求证:是的切线;(2)、求的长及图中阴影部分的面积.22. 某校课外小组为了研究对环境温度的影响,设计了如下的测量实验:用两个相同的集气瓶分别灌满空气和 , 测量了下午一段时间内两个集气瓶及环境温度的数值,并把收集到的数据绘制成如下的统计图.
(1)、求证:是的切线;(2)、求的长及图中阴影部分的面积.22. 某校课外小组为了研究对环境温度的影响,设计了如下的测量实验:用两个相同的集气瓶分别灌满空气和 , 测量了下午一段时间内两个集气瓶及环境温度的数值,并把收集到的数据绘制成如下的统计图. (1)、观察统计图,比较瓶、空气瓶中温度的高低,并说出室外温度下降时,哪个瓶中的温度下降较慢;(2)、根据统计图,说出对环境温度起到什么作用.(3)、为了减少地球表面平均温度上升,人类需要采取什么措施(写出一条即可)?23. 运行在某区段的高铁动车组对二等座实施浮动票价.二等座的基准票价为100元,按照基准票价售票时,上座率为60%.试运行阶段实施表明,票价在基准票价基础上每上浮10元,则上座率减少5个百分点;如果票价在基准票价基础上每下降10元,则上座率增加10个百分点.如:票价为110元时,上座率为55%;票价为90元时,上座率为70%.在实施浮动票价期间,保证上座率不低于30%.
(1)、观察统计图,比较瓶、空气瓶中温度的高低,并说出室外温度下降时,哪个瓶中的温度下降较慢;(2)、根据统计图,说出对环境温度起到什么作用.(3)、为了减少地球表面平均温度上升,人类需要采取什么措施(写出一条即可)?23. 运行在某区段的高铁动车组对二等座实施浮动票价.二等座的基准票价为100元,按照基准票价售票时,上座率为60%.试运行阶段实施表明,票价在基准票价基础上每上浮10元,则上座率减少5个百分点;如果票价在基准票价基础上每下降10元,则上座率增加10个百分点.如:票价为110元时,上座率为55%;票价为90元时,上座率为70%.在实施浮动票价期间,保证上座率不低于30%. (1)、设该列车二等座上座率为 , 实际票价为x元,写出y关于x的函数解析式,并写出自变量x的取值范围;(2)、请你用适当的函数解析式表示该列车二等座售票收入的变化规律;(3)、在不超载的情况下,请你帮助该列车的经营单位确定一个合理的价格,使得二等座售票收入最多.24. 我们已经研究过等腰三角形和直角三角形这两种特殊的三角形.其实,特殊的三角形很多比如,一个内角等于另一个内角的2倍的三角形也是一类特殊的三角形,我们把这类三角形叫做“二倍角三角形”,请按照下列要求研究“二倍角三角形”.
(1)、设该列车二等座上座率为 , 实际票价为x元,写出y关于x的函数解析式,并写出自变量x的取值范围;(2)、请你用适当的函数解析式表示该列车二等座售票收入的变化规律;(3)、在不超载的情况下,请你帮助该列车的经营单位确定一个合理的价格,使得二等座售票收入最多.24. 我们已经研究过等腰三角形和直角三角形这两种特殊的三角形.其实,特殊的三角形很多比如,一个内角等于另一个内角的2倍的三角形也是一类特殊的三角形,我们把这类三角形叫做“二倍角三角形”,请按照下列要求研究“二倍角三角形”. (1)、在直角三角形中,是二倍角三角形的有 ▲ ;用没有刻度的直尺和圆规作一个不含直角的二倍角三角形(不要求写作法,保留作图痕迹),(2)、如图,已知中,的对边分别为a,b,c.
(1)、在直角三角形中,是二倍角三角形的有 ▲ ;用没有刻度的直尺和圆规作一个不含直角的二倍角三角形(不要求写作法,保留作图痕迹),(2)、如图,已知中,的对边分别为a,b,c.①若 , 请提出a,b,c的等量关系的一个猜想,并加以证明;
②请从边的等量关系角度提出二倍角三角形的一个判定猜想,并加以证明.
(3)、是否存在三边长依次为连续自然数的“二倍角三角形”?如果存在,直接写出三边的长,如果不存在,请说明理由.