浙江省衢州市衢江区2022年中考第一次模拟数学试卷
试卷更新日期:2022-05-13 类型:中考模拟
一、单选题
-
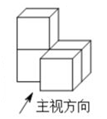
1. 2的绝对值是( )A、2 B、-2 C、 D、2. 如图是由4个大小相同的立方块搭成的几何体,这个几何体的主视图是( )
 A、
A、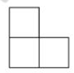 B、
B、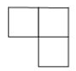 C、
C、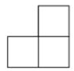 D、
D、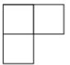 3. 截至2022年3月24日,“祝融号”火星车在距离地球277000000千米的火星表面工作306个火星日,数据277000000用科学记数法可表示为( )A、277×106 B、27.7×107 C、2.77×108 D、0.277×1094. 下列运算正确的是( )A、 B、 C、 D、5. 一个布袋里放有3个红球、2个白球和2个蓝球,它们除颜色外其余都相同.从布袋中任意摸出1个球,摸到红球的概率是( )A、 B、 C、 D、6. 如图,在中, , , 则的度数为( )
3. 截至2022年3月24日,“祝融号”火星车在距离地球277000000千米的火星表面工作306个火星日,数据277000000用科学记数法可表示为( )A、277×106 B、27.7×107 C、2.77×108 D、0.277×1094. 下列运算正确的是( )A、 B、 C、 D、5. 一个布袋里放有3个红球、2个白球和2个蓝球,它们除颜色外其余都相同.从布袋中任意摸出1个球,摸到红球的概率是( )A、 B、 C、 D、6. 如图,在中, , , 则的度数为( )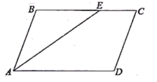 A、35° B、45° C、55° D、65°7. 不等式2x﹣6>0的解集在数轴上表示正确的是( )A、
A、35° B、45° C、55° D、65°7. 不等式2x﹣6>0的解集在数轴上表示正确的是( )A、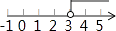 B、
B、 C、
C、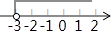 D、
D、 8. 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为:( )
8. 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为:( )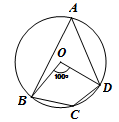 A、50° B、80° C、100° D、130°9. 如图,点是反比例函数的图象上的一个动点,以点为圆心,为半径的圆与轴交于点 , 延长交圆于点 , 连结 , 则的面积是( )
A、50° B、80° C、100° D、130°9. 如图,点是反比例函数的图象上的一个动点,以点为圆心,为半径的圆与轴交于点 , 延长交圆于点 , 连结 , 则的面积是( ) A、3 B、 C、 D、10. 甲、乙两辆遥控车沿直线AC作同方向的匀速运动.甲、乙同时分别从A,B出发,沿轨道到达C处.已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处的距离分别为S1 , S2 , 函数关系如图所示.当两车的距离小于10米时,信号会产生相互干扰.那么t是下列哪个值时两车的信号会相互干扰( )
A、3 B、 C、 D、10. 甲、乙两辆遥控车沿直线AC作同方向的匀速运动.甲、乙同时分别从A,B出发,沿轨道到达C处.已知甲的速度是乙的速度的1.5倍,设t分钟后甲、乙两车与B处的距离分别为S1 , S2 , 函数关系如图所示.当两车的距离小于10米时,信号会产生相互干扰.那么t是下列哪个值时两车的信号会相互干扰( ) A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
11. 分解因式:.12. 二次根式中字母的取值范围是.13. 随着体育中考的临近,某校随机地调查了45名学生的跳远成绩,结果如下表所示:
跳远成绩
160
170
180
190
200
220
人数
3
9
6
9
15
3
则这些同学的跳远成绩的的众数为 , 中位数为.
14. 已知 , , , , 将此三角形绕旋转一周所形成的圆锥的侧面积是.15. 如图,在平面直角坐标系中,Rt△ABC的顶点A,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数y= (k>0,x>0)的图象经过AC的中点D,则k的值为 . 16. 如图1是传统的手工推磨工具,根据它的原理设计了右图的机械设备,磨盘半径 , 用长为的连杆将点与动力装置相连(大小可变),点在轨道上滑动,并带动磨盘绕点转动, , .
16. 如图1是传统的手工推磨工具,根据它的原理设计了右图的机械设备,磨盘半径 , 用长为的连杆将点与动力装置相连(大小可变),点在轨道上滑动,并带动磨盘绕点转动, , . (1)、如图2,当与相切时,则.(2)、若磨盘转动10周,则点在轨道上滑动的路径长是.
(1)、如图2,当与相切时,则.(2)、若磨盘转动10周,则点在轨道上滑动的路径长是.三、解答题
-
17. 计算:18. 先化简,再求值: ,从1,2,3这三个数中选择一个你认为适合的 代入求值.19. 定义:等腰三角形 , 如果腰长是底边长的两倍,则称三角形是等腰倍边三角形.
 (1)、如图1,在等腰倍边三角形中, , , 求和的值.(2)、如图2,平行四边形 , , 对角线交于点 , 分成的四个以为顶点的三角形中,若和为等腰倍边三角形,请你求出的值.20. 垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:
(1)、如图1,在等腰倍边三角形中, , , 求和的值.(2)、如图2,平行四边形 , , 对角线交于点 , 分成的四个以为顶点的三角形中,若和为等腰倍边三角形,请你求出的值.20. 垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:
根据图表解答下列问题:
(1)、在抽样数据中,产生的垃圾一共有多少吨?(2)、在抽样数据中,产生的有害垃圾有多少吨?并补全条形统计图.(3)、调查发现,在可回收物中塑料类垃圾占 , 每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?21. 如图,是的外接圆, , BD是的直径, , 与DB的延长线交于点P,连结AD. (1)、求证:是的切线;(2)、若 , , 求BD与的长.22. 3月14日,衢州进行了第一次全民核酸检测,某小区上午9点开始检测,设6个采样窗口,每个窗口采样速度相同,居民陆续到采集点排队,10点半排队完毕,小明就排队采样的时间和人数进行了统计,得到下表:
(1)、求证:是的切线;(2)、若 , , 求BD与的长.22. 3月14日,衢州进行了第一次全民核酸检测,某小区上午9点开始检测,设6个采样窗口,每个窗口采样速度相同,居民陆续到采集点排队,10点半排队完毕,小明就排队采样的时间和人数进行了统计,得到下表:时间(分)
0
15
30
45
75
90
95
100
110
人数(个)
60
115
160
195
235
240
180
120
0
小明把数据在平面直角坐标系里,描成点连成线,得到如图所示函数图象,在0~90分钟,是的二次函数,在90~110分钟,是的一次函数.
 (1)、如果是二次函数图象的顶点,求二次函数解析式(2)、若排队人数在220人及以上,即为满负荷状态,问满负荷状态的时间持续多长?(3)、采样进行45分钟后,为了减少扎堆排队的时间,社区要求10点15分后,采样可以随到随采,那么至少需新增多少个采样窗口?23. 已知二次函数 , ( , 为常数,).(1)、若 , 求二次函数的顶点坐标.(2)、若 , 设函数的对称轴为直线 , 求的值.(3)、点在函数图象上,点在函数图象上.若函数图象的对称轴在轴右侧,当 , 时,试比较 , 的大小.24. 在四边形中,与BD互相垂直且平分.
(1)、如果是二次函数图象的顶点,求二次函数解析式(2)、若排队人数在220人及以上,即为满负荷状态,问满负荷状态的时间持续多长?(3)、采样进行45分钟后,为了减少扎堆排队的时间,社区要求10点15分后,采样可以随到随采,那么至少需新增多少个采样窗口?23. 已知二次函数 , ( , 为常数,).(1)、若 , 求二次函数的顶点坐标.(2)、若 , 设函数的对称轴为直线 , 求的值.(3)、点在函数图象上,点在函数图象上.若函数图象的对称轴在轴右侧,当 , 时,试比较 , 的大小.24. 在四边形中,与BD互相垂直且平分. (1)、【推理探究】如图1,已知 , 点是线段上任意一点,交于点 , 垂足为点 , 求证:.(2)、【类比应用】如图2,已知 , 点在的延长线上,且 , 交的延长线于点 , , 求的值.(3)、【拓展延伸】如图3,已知 , 点是的三等分点,交直线于点 , 垂足为点 , , 求的值.
(1)、【推理探究】如图1,已知 , 点是线段上任意一点,交于点 , 垂足为点 , 求证:.(2)、【类比应用】如图2,已知 , 点在的延长线上,且 , 交的延长线于点 , , 求的值.(3)、【拓展延伸】如图3,已知 , 点是的三等分点,交直线于点 , 垂足为点 , , 求的值.