浙江省绍兴市新昌县2022年初中毕业生学业考试模拟数学试卷

试卷更新日期：2022-05-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，比-1大的数是（）

A、-4 B、-3 C、-2 D、0

查看试题解析
2. 北京冬奥村是2022年北京冬季奥运会、冬残奥会最大的非竞赛类场馆之一，总建筑面积约38.66万平方米，其中38.66万用科学记数法可表示为（）

A、 $0.3866 \times 1 0^{6}$ B、 $3.9 \times 1 0^{5}$ C、 $3.866 \times 1 0^{5}$ D、 $38.66 \times 1 0^{4}$

查看试题解析
3. 如图是一个由5个小正方体和1个圆锥组成的立体图形，这个立体图形的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 如图所示为一副普通扑克牌中的13张黑桃牌，将它们洗匀后正面向下放在桌子上，从中任意抽取一张，抽出的牌点数是5的倍数的概率为（）

A、 $\frac{1}{13}$ B、 $\frac{2}{13}$ C、 $\frac{1}{10}$ D、 $\frac{1}{5}$

查看试题解析
5. 若点P在一次函数 $y = 2 x + 1$ 的图象上，点P的坐标可能是（）

A、 $(- 1 ， 0)$ B、 $(0 ， - 1)$ C、 $(1 ， 3)$ D、 $(2 ， 4)$

查看试题解析
6. 如图是甲和乙两位同学用尺规作∠AOB的平分线的图示，对于两人不同的作法，下列说法正确的是（）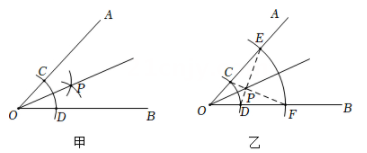

A、甲对乙不对 B、甲乙都对 C、甲不对乙对 D、甲乙都不对

查看试题解析
7. 如图是沙漏示意图（数据如图），上下两部分为全等三角形，将上半部分填满沙子后，在沙子下落至如图位置时，AB的长为多少？（正在下落的沙子忽略不计）（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
8. 二次函数 $y = {(x + k)}^{2} + h$ 的图象与x轴的交点的横坐标分别为-1和3，则 $y = {(x + k + 2)}^{2} + h$ 的图象与x轴的交点的横坐标分别为（）

A、-3和1 B、1和5 C、-3和5 D、3和5

查看试题解析
9. 将正方形纸片按图1方式依次对折得图2的△ABC，点D是AC边上一点，沿线段BD剪开展开后得到一个正方形，则点D应满足（）

A、 $A D = A B$ B、 $B D ⊥ A C$ C、 $D B = 2 A D$ D、 $∠ A D B = 60 °$

查看试题解析
10. 如图1，在矩形ABCD中，点E，F，G分别是边AD，BC，AB的中点，连结EF， $B C = 6$ ，点H是EF上一动点，设FH的长为x，GH与BH长度的和为y.图2是y关于x的函数图象，点P为图象上的最低点，则函数图象的右端点Q的坐标为（）

A、 $(2 ， 3 + \sqrt{13})$ B、 $(3 ， 5 + \sqrt{13})$ C、 $(3 ， 3 \sqrt{2} + \sqrt{10})$ D、 $(4 ， 5 + \sqrt{13})$

查看试题解析

二、填空题

11. 分解因式： $4 a b - 2 a =$ .

查看试题解析
12. 如图是北京冬奥会开幕式的巨型雪花状主火炬塔，此设计体现了环保低碳理念，它的主体形状呈正六边形，若点A，B，C是正六边形的三个顶点，则 $c o s ∠ A B C =$ .

查看试题解析
13. 某商品先按批发价a元提高20%零售，后又按零售价降低10%出售，则它最后的单价是元．

查看试题解析
14. 庆祝虎年，小明将一副七巧板拼成了如图的“回头虎”，则图中 $A B =$ .

查看试题解析
15. 如图，在△ABC中， $A B = A C$ ，点A在反比例函数 $y = \frac{k}{x} (k < 0 ， x > 0)$ 的图象上，点B，C在x轴上， $O C = \frac{1}{6} B C$ ，延长AC交y轴于点D，若△OCD的面积等于1，则k的值为.

查看试题解析
16. 在△ABC中，∠A=60°，点P和点Q分别是边AC和BC上的两个动点，分别连结BP和PQ，把△ABC分割成三个三角形，若分割成的这三个三角形都是等腰三角形，则∠ABC的度数可以是.

查看试题解析

三、解答题

17.

(1)、计算： $| - 3 | + {(- 2022)}^{0} - 4 t a n 45 °$

(2)、解不等式组： ${\begin{array}{l} x + 2 > - 4 \\ 2 x - 3 < 5 \end{array}$

查看试题解析
18. 某校组织学生进行“青年大学习”知识竞赛活动，竞赛成绩分为ABCD四个等级，根据某班竞赛结果分别制作了条形统计图和扇形统计图，请根据相关信息，解答下列问题：

(1)、求该班学生的总人数，并补全条形统计图.

(2)、求出扇形统计图中C等级所对应的扇形圆心角度数.

(3)、已知全校共400名学生，现选取每班知识竞赛A等级的学生参加校级竞赛，请你估算参加校级竞赛的人数.

查看试题解析
19. 如图是一种单人网球训练器示意图，横杆 $A B = 0.5 m$ ， $A B ⊥ A C$ ，点D表示网球的位置，横杆可绕点A旋转，通过旋转横杆，调节网球的高度，从而适应不同高度的人进行训练.现旋转AB，将点B旋转至点 $B'$ ，使 $∠ C A B' = 126 °$ .（ $s i n 36 ° \approx 0.588$ ， $c o s 36 ° \approx 0.809$ ， $t a n 36 ° \approx 0.727$ ， $π \approx 3.142$ ）

(1)、求横杆端点B的运动路径长.（结果精确到0.01m）

(2)、求网球上升的高度.（结果精确到0.01m）

查看试题解析
20. 如图， $A B ∥ C D$ ， $B P ⊥ C P$ ，点P是AD中点， $∠ A B C = 100 °$ .

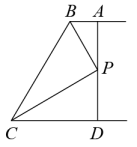(1)、求∠CBP的度数.

(2)、若点P到直线AB的距离为6，求点P到BC的距离.

查看试题解析
21. 为节约用水，某市居民生活用水按级收费，水费分为三个等级（如图）；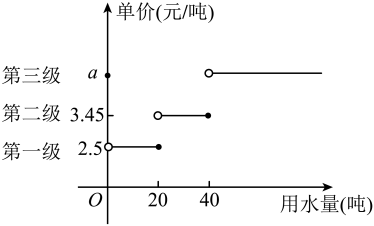

例如：某户用水量为35吨，则水费为20×2.5+（30-20）×3.45=101.75（元）.

(1)、若某住户收到一张自来水总公司水费专用发票，其中上期抄表数为587吨，本期抄表数为617吨，请计算本期该用户应付的水费.

(2)、若该住户的用水量为x吨 $(20 < x ≤ 40)$ ，应付水费为y元，求出y关于x的函数表达式.

(3)、小明爸爸收到水费短信通知：2022年2月本期用水量为45吨，水费为150.5元.根据此通知求出第三级收费标准a的值.

查看试题解析
22. 一个球从地面竖直向上弹起时的速度为10m/s，经过t（s）时球的高度为h（m）.已知物体竖直上抛运动中， $h = v_{0} t - \frac{1}{2} g t^{2}$ （ $v_{0}$ 表示物体运动上弹开始的速度，g表示重力系数，取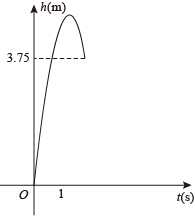 $g = 10 m / s^{2}$ ）.

(1)、写出h（m）关于t（s）的二次函数表达式.

(2)、求球从弹起到最高点需要多少时间，最高点的高度是多少？

(3)、若球在下落至 $h = 3.75 m$ 处时，遇一夹板（这部分运动的函数图象如图所示），球以遇到夹板时的速度再次向上竖直弹起，然后落回地面.求球从最初10m/s弹起到落回地面的时间.

查看试题解析

23. 在学习三角形高线时，发现三角形三条高线交于一点，我们把这个交点叫做三角形的垂心.课后小明同学继续探究，上网搜索得到了三角形重心的一条性质，制作了如下表格进行探究.

三角形关型	直角三角形	锐角三角形	钝角三角形
垂心的位置	直角顶点	①	在三角形外部
垂心的性质	三角形任意顶点到垂心的距离等于外心到对边的距离的两倍.
图形	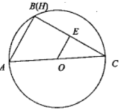图1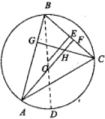	图2

(1)、表格中①处应填：.

(2)、小明先选择了直角三角形来探究重心的性质，写出了已知求证，请完成证明.

已知：如图1，⊙O是 $R t △ A B C$ 的外接圆， $∠ B = 90 °$ ， H是 $△ A B C$ 的垂心， $O E ⊥ B C$ ，垂足为E.

求证： $A H = 2 O E$ .

(3)、如图2，⊙O是锐角三角形ABC的外接圆，高线AF与高线CG交于点H，

O E ⊥ B C

于点E，为了证明

A H = 2 O E

.小明想把锐角三角形的问题转化为直角三角形，为此他过点B作了⊙O的直径BD，请继续小明的思路证明.

查看试题解析

24. 如图1，在菱形ABCD中， $A B = 5$ ， $s i n ∠ A B C = \frac{4}{5}$ ， $C N ⊥ A D$ 于点N，点P是边AD上的一个动点，连结CP，过点P作 $P Q ⊥ C P$ ，交直线A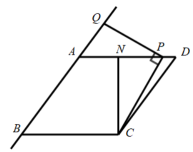B于点Q.

(1)、求CN的长.

(2)、当点P在DN上运动且满足 $\frac{C P}{P Q} = \frac{4}{3}$ 时，求DP的长.

(3)、如图2，若点E为边AB的中点，将△CDP沿CP翻折得F到△CFP，连结EF，AF，DF，△AEF的面积有可能为1吗？如果可能，求出DF的长；如果不可能，请说明理由.

查看试题解析