浙江省宁波市慈溪市2022年中考数学二模拟试卷

试卷更新日期：2022-05-13 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的倒数是（）

A、 $3$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、-3

查看试题解析
2. 据新华体育报道，国际奥委会新闻发言人在新闻发布会上透露，北京冬奥会开幕式中国大陆地区观看人数约3.16亿人. 其中3.16亿用科学记数法表示为（）

A、 $3.16$ B、 $31.6 \times 1 0^{7}$ C、 $3.16 \times 1 0^{8}$ D、 $0.316 \times 1 0^{9}$

查看试题解析
3. 下列计算正确的是（）

A、 $2^{2} + 2^{3} = 2^{5}$ B、 $2^{3} - 2^{2} = 2$ C、 $2^{3} \cdot 2^{2} = 2^{5}$ D、 $2^{- 1} = - 2$

查看试题解析
4. 如图所示的图形是由7个完全相同的小正方体组成的立体图形，则下面四个平面图形中不是这个立体图形的三视图的是（）

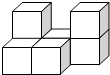A、 B、 C、 D、

查看试题解析
5. 不透明的袋子中装有三个小球，上面分别写着“1”，“2”，“2”，三个小球除数字外无其他差别.从中随机摸出一个小球，记录数字，不放回，再从中随机摸出一个小球，记录其数字，这两个小球上的数字刚好都是偶数的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{6}$

查看试题解析
6. 若二次根式 $\sqrt{1 - x}$ 在实数范围内有意义，则下列各数中， x可取的值是（）

A、4 B、 $π$ C、 $\sqrt{2}$ D、1

查看试题解析
7. 为了解邮政企业4月份收入的情况，随机抽取了25家邮政企业，获得了它们4月份收入（单位：百万元）的数据，并绘制成了频数直方图（如图，数据分成5组： $6 \leq x < 8$ ， $8 \leq x < 10$ ， $10 \leq x < 12$ ， $12 \leq x < 14$ ， $14 \leq x \leq 16$ ），现已知在 $10 \leq x < 12$ 这一组的数据是：10.0，10.0，10.1，10.9，10.9，11.5，11.6，11.8.则这25家邮政企业4月份收入的中位数是（）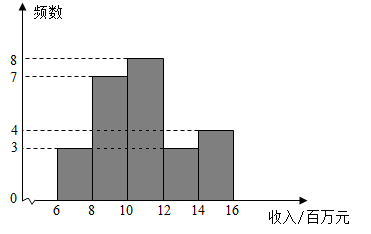

A、10.0 B、10.1 C、10.9 D、11.5

查看试题解析
8. 如图，在 $△ A B C$ 中， $O$ 为 $A C$ 边上一点，以 $O$ 为圆心， $O C$ 为半径的半圆切 $A B$ 于点 $B$ ，若 $A B = O C = \sqrt{2}$ ，则 $△ A B C$ 的面积为（）

A、 $1 + \frac{\sqrt{2}}{2}$ B、 $1 + \sqrt{2}$ C、 $\sqrt{2}$ D、 $\frac{3 \sqrt{2}}{2}$

查看试题解析
9. 当 $1 \leq x \leq 3$ 时，二次函数 $y = x^{2} - 2 a x + 3$ 的最小值为-1，则 $a$ 的值为（）

A、2 B、±2 C、2 或 $\frac{5}{2}$ D、2 或 $\frac{13}{6}$

查看试题解析
10. 如图，在正△ABC中，D、E分别为边AB、AC上的点，BD＝2CE，过点E作EF⊥DE交BC于点F，连结DF，若想求△ABC的周长，则只需知道下列哪个三角形的周长？该三角形是（）

A、△CEF B、△BDF C、△DEF D、△ADE

查看试题解析

二、填空题

11. 实数9的算术平方根为.

查看试题解析
12. 因式分解: $x^{2} - 16 =$ .

查看试题解析
13. 定义： [ $x]$ 表示不大于 $x$ 的最大整数， $(x)$ 表示不小于 $x$ 的最小整数，例如： $[2.3] = 2$ ， $(2.3) = 3 ， [- 2.3] = - 3 ， (- 2.3) = - 2$ . 则 $[1.7] + (- 1.7) =$ .

查看试题解析
14. 我国古代数学著作《张丘建算经》中著名的“百鸡问题”叙述如下：“鸡翁一，值钱五；鸡母一，值钱三；鸡雏三，值钱一；百钱买百鸡，则翁，母，雏各几何？”意思是公鸡五钱一只，母鸡三钱一只，小鸡一钱三只，要用一百钱买一百只鸡，问公鸡，母鸡，小鸡各多少只? 若现已知母鸡买18只，则公鸡买只，小鸡买只。

查看试题解析
15. 如图，△ABC中，AC＝BC，⊙O是△ABC的外接圆，BO的延长线交边AC于点D.当△ABD是等腰三角形时，∠C的度数为.

查看试题解析
16. 如图，在平面直角坐标系中，矩形OABC的边OA、OC分别在x、y轴上，点B的坐标为 $(3 ， 1.5)$ ，反比例函数 $y = \frac{k}{x}$ （k为常数， $k \neq 0$ ）的图象分别与边AB、BC交于点D、E，连结DE，将△BDE沿DE翻折得到 $△ B^{^{'}} D E$ ，连结OE，当 $∠ O E B^{'} = 90 °$ 时，k的值为.

查看试题解析

三、解答题

17.

(1)、计算： $(a + 3)^{2} - a (a + 6)$ .

(2)、解不等式组： ${\begin{array}{l} - 2 x + 1 \leq 9 \\ 3 + x > 0 \end{array}$

查看试题解析
18. 如图是由边长为1的小正方形构成的 $6 \times 6$ 的网格，点 $A ， B$ 均在格点上.

(1)、在图1中画出以 $A B$ 为对角线的正方形 $A C B D$ ，点 $C ， D$ 为格点.

(2)、在图2中画出以 $A B$ 为边且周长最大的平行四边形 $A B C D$ ，点 $C ， D$ 为格点 (画一个即可).

查看试题解析
19. “千年越窑，秘色慈溪”，为了解学生对慈溪秘色瓷的熟悉度，某校设置了非常了解，基本了解，很少了解，不了解四个选项，随机抽查了部分学生进行问卷调查，要求每名学生只选其中的一项，并将抽查结果绘制成如下不完整的统计图。

根据图中信息，解答下列问题：

(1)、本次接受问卷调查的学生有多少人?

(2)、求图2中 “很少了解” 的扇形圆心角的度数.

(3)、全校共有960名学生，请你估计全校学生中“非常了解”秘色瓷的学生共有多少人?

查看试题解析
20. 如图，在平面直角坐标系中，直线y＝kx＋3与x轴、y轴分别交于A，B两点.抛物线 $y = - \frac{1}{4} x^{2} + \frac{3}{2} x$ 经过点A，且交线段AB于点C， $B C = \sqrt{5}$ .

(1)、求k的值.

(2)、求点C的坐标.

(3)、向左平移抛物线，使得抛物线再次经过点C，求平移后抛物线的函数解析式.

查看试题解析
21. 图1为科研小组研制的智能机器，水平操作台为l，底座AB固定，高AB为50cm，始终与平台l垂直，连杆BC长度为60cm，机械臂CD长度为40cm，点B，C是转动点，AB，BC与CD始终在同一平面内，张角∠ABC可在60°与120°之间（可以达到60°和120°）变化，CD可以绕点C任意转动.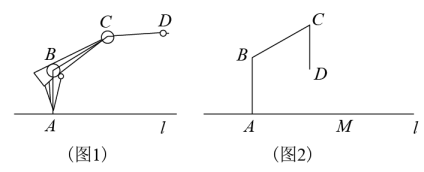

(1)、转动连杆BC，机械臂CD，使张角∠ABC最大，且CD∥AB，如图2，求机械臂臂端D到操作台l的距离DE的长.

(2)、转动连杆BC，机械臂CD，要使机械臂端D能碰到操作台l上的物体M，则物体M离底座A的最远距离和最近距离分别是多少？

查看试题解析
22. 甲、乙两人沿同一路线从 $A$ 地到 $B$ 地进行骑车训练，甲先出发，匀速骑行到 $B$ 地. 乙后出发，并在甲骑行25分钟后提速到原来速度的1.4倍继续骑行（提速过程的时间忽略不计)，结果乙比甲早12分钟到 $B$ 地. 两人距离 $A$ 地的路程 $y$ (单位：千米) 与甲骑行的时间 $x$ (单位：分钟)之间的关系如图所示.

(1)、求甲的速度和乙提速前的速度.

(2)、求 $A B$ 两地之间的路程.

查看试题解析
23. 如图

(1)、[证明体验]
如图1，在△ABC和△BDE中，点A，B、D在同一直线上，∠A＝∠CBE＝∠D＝90°，求证：△ABC∽△DEB.

(2)、如图2，图3，AD＝20，点B是线段AD上的点，AC⊥AD，AC＝4，连结BC，M为BC中点，将线段BM绕点B顺时针旋转90°至BE，连结DE.
[思考探究]如图2，当 $D E = \frac{\sqrt{2}}{2} M E$ 时，求AB的长.
[拓展延伸]如图3，点G过CA延长线上一点，且AG＝8，连结GE，∠G＝∠D，求ED的长.

查看试题解析
24. 如图1，在⊙O中，M为弦AB的中点，过点M作直径CD，E为线段OM上一点，连结AE并延长交⊙O于点F，连结BF，AE=BF.

(1)、证明：AC＝BF.

(2)、当 $E M ： O E = 2$ 时，求 $t a n ∠ E A B$ .

(3)、如图2，连结CF交AB于点G，当CD＝2时，设EM＝x， $A G \cdot A B = y$ ，求y关于x的函数解析式，并确定y的最大值.

查看试题解析