浙江省杭州市滨江区2022年中考一模数学试卷
试卷更新日期:2022-05-13 类型:中考模拟
一、单选题
-
1. cos60° 的值等于( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 已知 ,则 的余角是( )A、 B、 C、 D、4. 若反比例函数为常数,且的图象经过点 , 那么,该函数图象一定经过点( )A、 B、 C、 D、5. 如图,ABCD,若 , 则( )
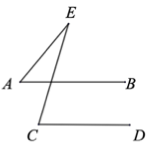 A、 B、 C、 D、6. 数据的方差是( )A、80 B、100 C、150 D、6007. 如图,AB是中的一条弦,半径于点 , 交于点D,点是上一点,若 , 则( )
A、 B、 C、 D、6. 数据的方差是( )A、80 B、100 C、150 D、6007. 如图,AB是中的一条弦,半径于点 , 交于点D,点是上一点,若 , 则( ) A、 B、 C、 D、8. 在四边形ABCD中,两对角线交于点O,若OA=OB=OC=OD,则这个四边形( )A、可能不是平行四边形 B、一定是菱形 C、一定是正方形 D、一定是矩形9. 如图,在中, , 分别以该直角三角形的三边为边,并在直线AB同侧作正方形 , 正方形 , 正方形 , 且点恰好在正方形的边上.其中表示相应阴影部分面积,若=1,则( )
A、 B、 C、 D、8. 在四边形ABCD中,两对角线交于点O,若OA=OB=OC=OD,则这个四边形( )A、可能不是平行四边形 B、一定是菱形 C、一定是正方形 D、一定是矩形9. 如图,在中, , 分别以该直角三角形的三边为边,并在直线AB同侧作正方形 , 正方形 , 正方形 , 且点恰好在正方形的边上.其中表示相应阴影部分面积,若=1,则( ) A、2 B、 C、3 D、10. 在平面直角坐标系中,二次函数是常数,的图象经过点.当时,;当时, , 则( )A、-1 B、 C、 D、1
A、2 B、 C、3 D、10. 在平面直角坐标系中,二次函数是常数,的图象经过点.当时,;当时, , 则( )A、-1 B、 C、 D、1二、填空题
-
11. 分解因式: = .12. 在平面直角坐标系中,将点向左平移3个单位后所得的点的坐标是.13. 若不等式组的解为 , 则的取值范围是.14. 在△ABC中,∠B=40°,∠C=34°,以B为圆心,以BA长为半径画弧,交BC边于点D,连接AD,则∠DAC=度.15. 有两辆车按1,2编号,舟舟和嘉嘉两人可任意选坐一辆车.则两人同坐2号车的概率为.16. 如图,点E是矩形边上一点,沿折叠,点恰好落在边上的点处,设 ,
 (1)、若点恰为边的中点,则.(2)、设 , 则y关于的函数表达式是.
(1)、若点恰为边的中点,则.(2)、设 , 则y关于的函数表达式是.三、解答题
-
17. 以下是小滨在解方程时的解答过程.
解:原方程可化为
解得原方程的解是.
小滨的解答是否有错误?如果有错误,请写出正确的解答过程.
18. 超市为制定今年第三季度功能饮料订购计划,销售部门查阅了去年第三季度某一周的饮料销售情况,并将其销售量绘制成如下的统计图:
请根据统计图回答以下问题:
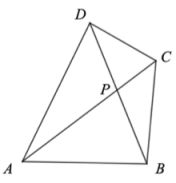
(1)、补全条形统计图.(2)、求扇形统计图中“能量饮料”部分的圆心角.(3)、请制定该超市今年第三季度的订购各类饮料数的计划(第三季度按13周计算).19. 在① , ② , ③这三个条件中选择其中一个,补充在下面的问题中,使命题正确,并证明.问题:如图,四边形的两条对角线交于P点,若 ▲ (填序号)
求证:.
 20. 某市政府计划建设一项水利工程,工程需要运送的土石方总量为立方米,某运输公司承担了运送土石方的任务.(1)、设该公司平均每天运送土石方总量为立方米,完成运送任务所需时间为天.
20. 某市政府计划建设一项水利工程,工程需要运送的土石方总量为立方米,某运输公司承担了运送土石方的任务.(1)、设该公司平均每天运送土石方总量为立方米,完成运送任务所需时间为天.①求关于的函数表达式.
②若时,求的取值范围.
(2)、若1辆卡车每天可运送土石方立方米,工期要求在80天内完成,公司至少要安排多少辆相同型号卡车运输?

