2022年初中数学苏科版《中考二轮复习》专题二 函数 2.3 二次函数
试卷更新日期:2022-05-12 类型:二轮复习
一、单选题
-
1. 函数y=﹣x2﹣2x+m的图象上有两点A(1,y1),B(2,y2),则( )A、y1<y2 B、y1>y2 C、y1=y2 D、y1、y2的大小不确定2. 当时, 二次函数的最小值为-1, 则的值为( )A、2 B、±2 C、2 或 D、2 或3. 将抛物线C1:y=(x-3)2+2向左平移3个单位长度,得到抛物线C2 , 抛物线C2与抛物线C3关于x轴对称,则抛物线C3的解析式为( ).A、y=x2-2 B、y=-x2+2 C、y=x2+2 D、y=-x2-24. 把二次函数y=ax2+bx+c(a>0)的图象作关于x轴的对称变换,所得图象的解析式为y=﹣a(x﹣1)2+2a,若(m﹣1)a+b+c≤0,则m的最大值是( )A、0 B、1 C、2 D、45. “数形结合”思想是数学学习的一个重大思想.通过巧妙运用几何代数的结合性有时能将某些难题迎刃而解.已知a,b,c,d均为实数,a2+b2=c2+d2 , 则abcd的最大值为( )A、 B、 C、1 D、26. “如果二次函数 的图像与 轴有两个交点,那么一元二次方程 有两个不相等的实数根.”请根据这句话的理解,解决以下问题;若 、 是关于 的方程 的两根,且 ,则 , , , 的大小关关系是( )A、 B、 C、 D、7. 抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.有下列结论:①关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;②﹣1<m<2;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 . 其中正确的个数是( )A、1 B、2 C、3 D、48. 已知二次函数y=a(x+1)(x﹣m)(a≠0,1<m<2),当x<﹣1时,y随x的增大而增大,则下列结论正确的是( )
①当x>2时,y随x的增大而减小;
②若图象经过点(0,1),则﹣1<a<0;
③若(﹣2022,y1),(2022,y2)是函数图象上的两点,则yl<y2;
④若图象上两点 , 对一切正数n,总有y1>y2 , 则1<m .
A、①② B、①③ C、①②③ D、①③④9. 如图,在中, , , , 动点从点开始沿边向以的速度移动(不与点重合),动点从点开始沿边向以的速度移动(不与点重合).如果、分别从、同时出发,那么经过( )秒,四边形的面积最小. A、0.5 B、1.5 C、3 D、410. 如图,二次函数的图象与x轴交于A,B两点,与y轴的正半轴交于点C,它的对称轴为直线.有下列结论:①;②;③;④当时,;⑤若、()是方程的两根,则方程的两根m、n(m<n)满足 , 且.其中,正确结论的个数是( )
A、0.5 B、1.5 C、3 D、410. 如图,二次函数的图象与x轴交于A,B两点,与y轴的正半轴交于点C,它的对称轴为直线.有下列结论:①;②;③;④当时,;⑤若、()是方程的两根,则方程的两根m、n(m<n)满足 , 且.其中,正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 已知二次函数y=ax2+bx+c的图象的顶点坐标为(1,m),与y轴的交点为(0,m-2),则a的值为.12. 已知抛物线 ( 为常数, )经过点 ,点 是x轴正半轴上的动点.点 在抛物线上,当 的最小值为 时,b的值为.13. 某快餐店销售A、B两种快餐,每份利润分别为12元、8元,每天卖出份数分别为40份、80份.该店为了增加利润,准备降低每份A种快餐的利润,同时提高每份B种快餐的利润.售卖时发现,在一定范围内,每份A种快餐利润每降1元可多卖2份,每份B种快餐利润每提高1元就少卖2份.如果这两种快餐每天销售总份数不变,那么这两种快餐一天的总利润最多是元.14. 如图,在平面直角坐标系中,O为坐标原点,点C为y轴正半轴上的一个动点,过点C的直线与二次函数 的图象交于A、B两点,且 ,P为 的中点,设点P的坐标为 ,写出y关于x的函数表达式为:.
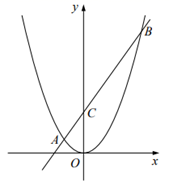 15. 如图,已知 ,在x轴上取 两点,使 ,把线段 交点A沿逆时针方向旋转 ,得线段 ,把线段 绕点B沿顺时针方向旋转 ,得线段 ,当 两点之间的距离最小时,点C的坐标为.
15. 如图,已知 ,在x轴上取 两点,使 ,把线段 交点A沿逆时针方向旋转 ,得线段 ,把线段 绕点B沿顺时针方向旋转 ,得线段 ,当 两点之间的距离最小时,点C的坐标为.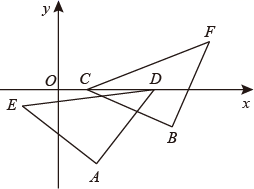 16. 如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2-6ax+5a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧,连接BD,则BD的最小值是.
16. 如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2-6ax+5a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧,连接BD,则BD的最小值是. 17. 如图,抛物线 与 轴交于 两点, 是以点 为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是.
17. 如图,抛物线 与 轴交于 两点, 是以点 为圆心,2为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是. 18. 如图,抛物线y = 的图象与坐标轴交于A、B、D , 顶点为E , 以AB为直径画半圆交y轴的正半轴于点C , 圆心为M , P是半圆上的一动点,连接EP , N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是 .
18. 如图,抛物线y = 的图象与坐标轴交于A、B、D , 顶点为E , 以AB为直径画半圆交y轴的正半轴于点C , 圆心为M , P是半圆上的一动点,连接EP , N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是 .
三、解答题
-
19. 旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金是x(元).发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.当每辆车的日租金为多少元时,每天的净收入最多?(注:净收入=租车收入管理费)
20. 甲、乙两人分别站在相距6米的A、B两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面1米的C处发出一球,乙在离地面1.5米的D处成功击球,球飞行过程中的最高点H与甲的水平距离AE为4米,现以A为原点,直线AB为x轴,建立平面直角坐标系(如图所示).求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度.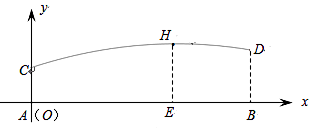 21. 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为 ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=﹣0.01x2﹣20x+30000(0≤x≤1000).
21. 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为 ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=﹣0.01x2﹣20x+30000(0≤x≤1000).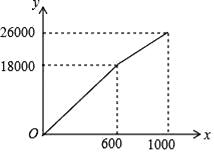 (1)、请直接写出k1、k2和b的值;(2)、设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求出绿化总费用W的最大值;(3)、若种草部分的面积不少于700m2 , 栽花部分的面积不少于100m2 , 请求出绿化总费用W的最小值.22. 某瓜果基地市场部为指导该基地某种蔬菜的生产销售,在对历年市场行情和生产情况进行调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图所示.注:两图中的每个实心点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低,图甲的图象是线段,图乙的图象是抛物线.
(1)、请直接写出k1、k2和b的值;(2)、设这块1000m2空地的绿化总费用为W(元),请利用W与x的函数关系式,求出绿化总费用W的最大值;(3)、若种草部分的面积不少于700m2 , 栽花部分的面积不少于100m2 , 请求出绿化总费用W的最小值.22. 某瓜果基地市场部为指导该基地某种蔬菜的生产销售,在对历年市场行情和生产情况进行调查的基础上,对今年这种蔬菜上市后的市场售价和生产成本进行了预测,提供了两个方面的信息,如图所示.注:两图中的每个实心点所对应的纵坐标分别指相应月份的售价和成本,生产成本6月份最低,图甲的图象是线段,图乙的图象是抛物线.请你根据图象提供的信息说明:
 (1)、在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价﹣成本)(2)、哪个月出售这种蔬菜,每千克的收益最大?说明理由;(3)、已知市场部销售该种蔬菜,4、5两个月的总收益为48万元,且5月份的销量比4月份的销量多2万公斤,求4、5两个月销量各多少万公斤?23. 如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)、在3月份出售这种蔬菜,每千克的收益是多少元?(收益=售价﹣成本)(2)、哪个月出售这种蔬菜,每千克的收益最大?说明理由;(3)、已知市场部销售该种蔬菜,4、5两个月的总收益为48万元,且5月份的销量比4月份的销量多2万公斤,求4、5两个月销量各多少万公斤?23. 如图,对称轴为直线x=2的抛物线经过点A(-1,0),C(0,5)两点,与x轴另一交点为B,已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.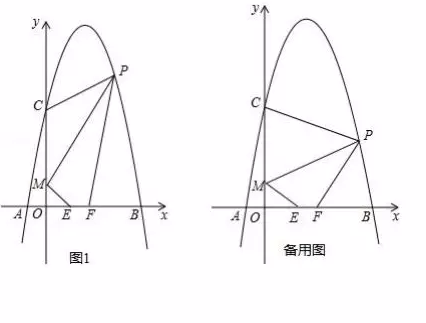 (1)、求此抛物线的解析式.(2)、当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.(3)、若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.24. 在平面直角坐标系中,直线y= x﹣2与x轴交于点B,与y轴交于点C,二次函数y= x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)、求此抛物线的解析式.(2)、当a=1时,求四边形MEFP面积的最大值,并求此时点P的坐标.(3)、若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.24. 在平面直角坐标系中,直线y= x﹣2与x轴交于点B,与y轴交于点C,二次函数y= x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.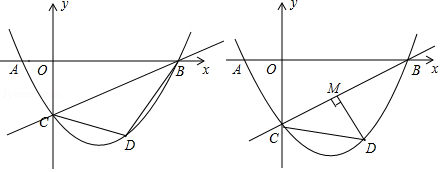 (1)、求二次函数的表达式;(2)、如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)、如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.25. 在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.
(1)、求二次函数的表达式;(2)、如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;(3)、如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.25. 在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.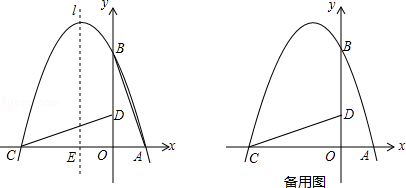 (1)、求抛物线的解析式;(2)、若点P是第二象限内抛物线上的动点,其坐标为t,
(1)、求抛物线的解析式;(2)、若点P是第二象限内抛物线上的动点,其坐标为t,①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似点P的坐标;
②是否存在一点P,使△PCD得面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
26. 如图,已知抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H. (1)、求该抛物线的解析式;(2)、若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;(3)、如图(2),若E是线段AD上的一个动点( E与A.D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
(1)、求该抛物线的解析式;(2)、若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;(3)、如图(2),若E是线段AD上的一个动点( E与A.D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.