备考浙教版中考数学题型专项训练数与式选择题专练

试卷更新日期：2022-05-12 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 如图，正方形ABCD被分成五个面积相等的矩形，若FG=4，则正方形的面积为（）

A、64 B、 $\frac{225}{4}$ C、49 D、36

查看试题解析
2. 观察一列数： $\frac{1}{2} ， - \frac{3}{4} ， \frac{5}{6} ， - \frac{7}{8}$ ， …，按此规律，这一列数的第2022个数是（）

A、 $- \frac{4043}{4044}$ B、 $\frac{4043}{4044}$ C、 $\frac{2022}{4044}$ D、 $\frac{2023}{4044}$

查看试题解析
3. 如图，大矩形分割成五个小矩形，④号、⑤号均为正方形，其中⑤号正方形边长为1．若②号矩形的长与宽的差为2，则知道哪个小矩形的周长，就一定能算出这个大矩形的面积（）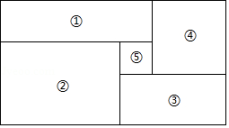

A、①或③ B、② C、④ D、以上选项都可以

查看试题解析
4. 已知x，y为实数，且满足 $x^{2} - x y + 4 y^{2} = 4$ ，记 $u = x^{2} + x y + 4 y^{2}$ 的最大值为M，最小值为m，则 $M + m =$ （）.

A、 $\frac{40}{3}$ B、 $\frac{64}{15}$ C、 $\frac{136}{15}$ D、 $\frac{31}{5}$

查看试题解析
5. 在数轴上，点M、N分别表示数m，n.则点M、N之间的距离为 $| m - n |$ .已知点A，B，C，D在数轴上分别表示的数为a，b，c，d.且 $| a - c | = | b - c | = 2 ， \frac{2}{5} | d - a | = 1 (a \neq b)$ ，则线段 $B D$ 的长度为（）

A、4.5 B、1.5 C、6.5或1.5 D、4.5或1.5

查看试题解析
6. 下列说法正确的是（）

A、 $\frac{\sqrt{2}}{2}$ 是分数 B、16的平方根是±4，即 $\sqrt{16} = \pm 4$ C、8.30万精确到百分位 D、若 $\sqrt{a - 2022} + | b + 1 | = 0$ ，则 $b^{a} = 1$

查看试题解析
7. 如图所示，由一些点组成形如三角形的图形，每条“边”（包括两个顶点）有n（n>1）个点，当n=11时，该图形总的点数是（）

A、27 B、30 C、33 D、36

查看试题解析
8. 一段跑道长100米，两端分别记为点A、B．甲、乙两人分别从A、B两端同时出发，在这段跑道上来回练习跑步，甲跑步的速度是6m/s，乙跑步的速度为4m/s，练习了足够长时间，他们经过了多次相遇，相遇点离A端不可能是（）

A、60米 B、0米 C、20米 D、100米

查看试题解析
9. 已知a₁+a₂＝1，a₂+a₃＝2，a₃+a₄＝﹣3，a₄+a₅＝﹣4，a₅+a₆＝5，a₆+a₇＝6，a₇+a₈＝﹣7，a₈+a₉＝﹣8，……，a₉₉+a₁₀₀＝﹣99，a₁₀₀+a₁＝﹣100，那么a₁+a₂+a₃+……+a₁₀₀的值为（）

A、﹣48 B、﹣50 C、﹣98 D、﹣100

查看试题解析
10. 斐波那契螺旋线，也称“黄金螺旋线”，它可以通过分别以1，1，2，3，5，…为半径，依次作圆心角为90°的扇形弧线画出来（如图）．第1步中扇形的半径是1cm，按如图所示的方法依次画，第8步所画扇形的弧长为（）

A、 $4 π$ B、 $\frac{21}{2} π$ C、 $17 π$ D、 $\frac{55}{2} π$

查看试题解析
11. 二次函数y= $\frac{2}{3}$ x²的图象如图所示，点A₀位于坐标原点，A₁ ， A₂ ， A₃ ， …，A₂₀₂₃在y轴的正半轴上，B₁ ， B₂ ， B₃ ， …，B₂₀₂₃在二次函数y= $\frac{2}{3}$ x²第一象限的图象上，若△A₀B₁A₁ ， △A₁B₂A₂ ， △A₂B₃A₃ ， …，△A₂₀₂₂B₂₀₂₃A₂₀₂₃都是等边三角形，则△A₂₀₂₂B₂₀₂₃A₂₀₂₃的周长是（）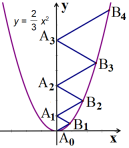

A、6069 B、6066 C、6063 D、6060

查看试题解析
12. 如图，直线 $y = x + 1$ 与x轴、y轴分别相交于点A、B，过点B作 $B C ⊥ A B$ ，使 $B C = 2 B A$ ，将 $△ A B C$ 绕点O顺时针旋转，每次旋转 $90 °$ ，则第2021次旋转结束时，点C的对应点 $C$ 落在反比例函数 $y = \frac{k}{x}$ 的图象上，则k的值为（）

A、-4 B、4 C、-6 D、6

查看试题解析
13. 如图，已知长方形纸板的边长 $D E = 10$ ， $E F = 11$ ，在纸板内部画 $R t △ A B C$ ，并分别以三边为边长向外作正方形，当边 $H I$ 、 $L M$ 和点K、J都恰好在长方形纸板的边上时，则 $△ A B C$ 的面积为（）

A、6 B、 $\frac{11}{2}$ C、 $\frac{25}{4}$ D、 $3 \sqrt{5}$

查看试题解析
14. 将△OBA按如图方式放在平面直角坐标系中，其中∠OBA=90°，∠A=30°，顶点A的坐标为 $(1 ， \sqrt{3})$ ，将△OAB绕原点逆时针旋转，每次旋转60°，则第2023次旋转结束时，点A对应点的坐标为（）

A、 $(- 1 ， \sqrt{3})$ B、 $(- \sqrt{3} ， 1)$ C、 $(- \frac{\sqrt{3}}{3} ， 1)$ D、 $(- 1 ， \frac{\sqrt{3}}{3})$

查看试题解析
15. 把五张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个大长方形(长为m，宽为n内(如图②)，大长方形未被卡片覆盖的部分用阴影表示.当m不变，n变长时，阴影部分的面积差总保持不变，则a，b应满足的关系为（ )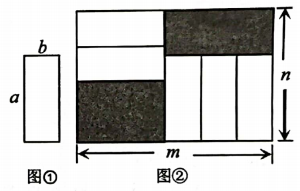

A、a=5b B、a=3b C、a=2b D、 $a = \frac{3}{2} b$

查看试题解析
16. 已知一列数a₁、a₂、a₃ ， …，满足 $a_{m} \cdot a_{n} = a_{m + n}$ (m，n为正整数)、例如： $a_{1} \cdot a_{2} = a_{1 + 2} = a_{3} ， a_{2} \cdot a_{2} = a_{2 + 2} = a_{4}$ ，若 $a_{1} < 0 ， a_{2} = 4$ ，则 $a_{2021}$ 的值是（ )

A、4042 B、 $- 2^{2020}$ C、 $2^{2021}$ D、 $- 2^{2021}$

查看试题解析
17. 如图，已知正方形的边长为24厘米，甲，乙两动点分别从正方形ABCD的顶点D，B同时沿正方形的边开始移动，甲点按顺时针方向环行，乙点按逆时针方向环行，若乙的速度为9厘米/秒，甲的速度为3厘米/秒，当它们运动了2022秒时，它们在正方形边上相遇了（）

A、252 次 B、253次 C、254次 D、255次

查看试题解析
18. “杨辉三角”（如图），也叫“贾宪三角”，是中国古代数学无比睿智的成就之一，被后世广泛运用．用“杨辉三角”可以解释 $(a + b)^{n}$ （ $n$ ＝ $1$ ， $2$ ， $3$ ， $4$ ， 5，6）的展开式的系数规律．例如，在“杨辉三角”中第3行的3个数 $1$ ， $2$ ， $1$ ，恰好对应着 $(a + b)^{2}$ 展开式 $a^{2} + 2 a b + b^{2}$ 中各项的系数；第4行的4个数 $1$ ， $3$ ， $3$ ， $1$ ，恰好对应着 $(a + b)^{3}$ 展开式 $a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ 中各项的系数，等等．当n是大于6的自然数时，上述规律仍然成立，那么 $(a - \frac{1}{a})^{9}$ 展开式中 $a^{7}$ 的系数是（）

A、 $9$ B、 $- 9$ C、 $36$ D、 $- 36$

查看试题解析
19. 如图，将图1中的长方形纸片前成（1）号、（2）号、（3）号、（4）号正方形和（5）号长方形，并将它们按图2的方式无重叠地放入另一个大长方形中，若需求出没有覆盖的阴影部分的周长，则下列说法中错误的是（）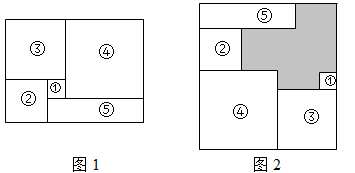

A、只需知道图 1 中大长方形的周长即可 B、只需知道图 2 中大长方形的周长即可 C、只需知道（3）号正方形的周长即可 D、只需知道（5）号长方形的周长即可

查看试题解析
20. 如图，数轴上的点O和点A分别表示0和10，点P是线段OA上一动点.点P沿O→A→O以每秒2个单位的速度往返运动1次，B是线段OA的中点，设点P运动时间为t秒（t不超过10秒）.若点P在运动过程中，当PB＝2时，则运动时间t的值为（）

A、 $\frac{3}{2}$ 秒或 $\frac{5}{2}$ 秒 B、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒或 $\frac{13}{2}$ 秒或 $\frac{15}{2}$ 秒 C、3秒或7秒或 $\frac{13}{2}$ 秒或 $\frac{17}{2}$ 秒 D、 $\frac{3}{2}$ 秒或 $\frac{7}{2}$ 秒或 $\frac{13}{2}$ 秒或 $\frac{17}{2}$ 秒

查看试题解析
21. 有理数 $a ， b ， c$ 在数轴上对应的点的位置如图所示，则下列各式正确的个数有（）
① $a b c > 0$ ；② $a + c < b$ ；③ $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = - 1$ ；④ $| a - b | - | b - c | = | a - c |$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析
22. 已知a=8³³ ， b=16²⁵ ， c=32¹⁹ ，则有（）

A、a<b<c B、c<b<a C、c<a<b D、a<c<b

查看试题解析
23. 当x=-6，y= $\frac{1}{6}$ 时，x²⁰¹⁸y²⁰¹⁹的值为（）

A、 $\frac{1}{6}$ B、- $\frac{1}{6}$ C、6 D、-6

查看试题解析
24. 如图，点M在线段AN的延长线上，且线段MN＝20，第一次操作：分别取线段AM和AN的中点M₁ ， N₁；第二次操作：分别取线段AM₁和AN₁的中点M₂ ， N₂；第三次操作：分别取线段AM₂和AN₂的中点M₃ ， N₃；…连续这样操作10次，则M₁₀N₁₀＝（）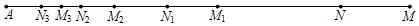

A、2 B、 $\frac{20}{2^{9}}$ C、 $\frac{20}{2^{10}}$ D、 $\frac{20}{2^{11}}$

查看试题解析
25. 观察下列等式： $3^{1} = 3 ， 3^{2} = 9 ， 3^{3} = 27 ， 3^{4} = 81 ， 3^{5} = 243 ， 3^{6} = 729 ， 3^{7} = 2187 ， \cdot \cdot \cdot$ ，解答下面问题： $3 + 3^{2} + 3^{3} + 3^{4} + ⋯ + 3^{2022}$ 的末位数字是（）

A、0 B、2 C、3 D、9

查看试题解析
26. 已知动点A在数轴上从原点开始运动，第一次向左移动1厘米，第二次向右移动2厘米，第三次向左移动3厘米，第四次向右移动4厘米，……，移动第2022次到达点B，则点B在点A点的（）

A、左侧1010厘米 B、右侧1010厘米 C、左侧1011厘米 D、右侧1011厘米

查看试题解析
27. 观察图中给出的四个点阵，s表示每个点阵中的点的个数，按照图形中的点的个数变化规律，猜想第n个点阵中的点的个数s为（）．

A、3n－2 B、3n－1 C、4n＋1 D、4n－3

查看试题解析
28. 为了求 $1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2020}$ 的值，可令 $S = 1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2020}$ ，则 $2 S = 2 + 2^{2} + 2^{3} + 2^{4} + ⋯ + 2^{2021}$ ，因此 $2 S - S = 2^{2021} - 1$ ，所以 $1 + 2 + 2^{2} + 2^{3} + ⋯ + 2^{2020} = 2^{2021} - 1$ ．仿照以上推理计算出 $1 + 5 + 5^{2} + 5^{3} + ⋯ + 5^{2020}$ 的值是（）

A、 $5^{2020} - 1$ B、 $5^{2021} - 1$ C、 $\frac{5^{2020} - 1}{4}$ D、 $\frac{5^{2021} - 1}{4}$

查看试题解析
29. 如图，A、O、B两点在数轴上对应的数分别为﹣20、0、40，C点在A、B之间，在A、B两点处各放一个挡板，M、N两个小球同时从C处出发，M以2个单位/秒的速度向数轴负方向运动，N以4个单位/秒的速度向数轴正方向运动，碰到挡板后则反方向运动，速度大小不变．设两个小球运动的时间为t秒钟（0＜t＜40），当M小球第一次碰到A挡板时，N小球刚好第一次碰到B挡板．则：①C点在数轴上对应的数为0；②当10＜t＜25时，N在数轴上对应的数可以表示为80﹣4t；③当25＜t＜40时，2MA+NB始终为定值160；④只存在唯一的t值，使3MO＝NO，以上结论正确的有（　　）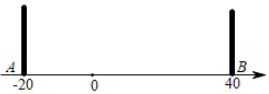

A、①②③④ B、①③ C、②③ D、①②④

查看试题解析
30. 已知a= $\frac{1}{\sqrt{2} + 1}$ ，b= $\frac{1}{\sqrt{2} - 1}$ ，则a与b的关系是（）

A、相等 B、互为相反数 C、互为倒数 D、平方值相等

查看试题解析

备考浙教版中考数学题型专项训练 数与式选择题专练

一、单选题

备考浙教版中考数学题型专项训练数与式选择题专练