人教版数学八年级下册期末复习测试题
试卷更新日期:2022-05-12 类型:期末考试
一、单选题
-
1. 二次根式 有意义时,x的取值范围是( )A、x≥1 B、x>1 C、x≤1 D、x≠12. 直角三角形的两条直角边的长分别为6和8,则斜边长为( )A、10 B、5 C、4 D、33. 下列根式中,最简二次根式的是( )A、 B、 C、 D、4. 在平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=40°,∠CBD=25°,则∠COD等于( )
 A、60° B、65° C、70° D、75°5. 平行四边形一定具有的性质是( )A、内角和为180° B、是中心对称图形 C、邻边相等 D、对角互补6. 我国古代算书《九章算术》中第九章第六题是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深葭长各几何?你读懂题意了吗?请回答水深______尺,葭长_____尺.解:根据题意,设水深OB=x尺,则葭长OA'=(x+1)尺.可列方程正确的是( )
A、60° B、65° C、70° D、75°5. 平行四边形一定具有的性质是( )A、内角和为180° B、是中心对称图形 C、邻边相等 D、对角互补6. 我国古代算书《九章算术》中第九章第六题是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深葭长各几何?你读懂题意了吗?请回答水深______尺,葭长_____尺.解:根据题意,设水深OB=x尺,则葭长OA'=(x+1)尺.可列方程正确的是( ) A、x2+52 =(x+1)2 B、x2+52 =(x﹣1)2 C、x2+(x+1)2 =102 D、x2+(x﹣1)2=527. 关于函数的图象,下列结论正确的是( )A、必经过点(1,2) B、与x轴交点的坐标为(0,-4) C、过第一、三、四象限 D、可由函数的图象平移得到8. 李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )A、
A、x2+52 =(x+1)2 B、x2+52 =(x﹣1)2 C、x2+(x+1)2 =102 D、x2+(x﹣1)2=527. 关于函数的图象,下列结论正确的是( )A、必经过点(1,2) B、与x轴交点的坐标为(0,-4) C、过第一、三、四象限 D、可由函数的图象平移得到8. 李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )A、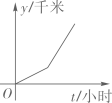 B、
B、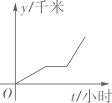 C、
C、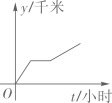 D、
D、 9. 疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如表:
9. 疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如表:金额/元
5
10
20
50
100
人数
6
17
14
8
5
则他们捐款金额的中位数是( )
A、17 B、14 C、10 D、2010. 弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:x/kg
0
1
2
3
4
5
y/cm
10
10.5
11
11.5
12
12.5
下列说法一定错误的是( )
A、x与y都是变量,且x是自变量,y是因变量 B、弹簧不挂重物时的长度为0cm C、物体质量每增加1kg,弹簧长度y增加0.5 cm D、所挂物体质量为7kg时,弹簧长度为13.5cm二、填空题
-
11. 若 ,则 .12. 如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile,它们离开港口一个半小时后相距30nmile,且知道“远航”号沿东北方向航行,那么“海天”号航行的方向是.
 13. 如图,在矩形ABCD中,已知AD=8cm,CD=6cm,对角线AC,BD相交于点O,E,F分别是AO,AD的中点,则AC=cm,EF=cm.
13. 如图,在矩形ABCD中,已知AD=8cm,CD=6cm,对角线AC,BD相交于点O,E,F分别是AO,AD的中点,则AC=cm,EF=cm. 14. 一次函数的图象经过原点,则y随x的增大而 .(填“增大”或“减小”)15. 如图,函数y=2x和y=ax+4的图象相交于点A(n,2),则不等式2x≥ax+4的解集为 .
14. 一次函数的图象经过原点,则y随x的增大而 .(填“增大”或“减小”)15. 如图,函数y=2x和y=ax+4的图象相交于点A(n,2),则不等式2x≥ax+4的解集为 . 16. 《九章算术》中,赵爽利用“弦图”(如图①)证明了勾股定理,类比此方法研究等边三角形(如图②):在等边三角形ABC中,如果∠BAD=∠CBE=∠ACF,那么△ABD的三边存在一定的数量关系,设BD=a,AD=b,AB=c,则这三边a,b,c满足的数量关系是 .
16. 《九章算术》中,赵爽利用“弦图”(如图①)证明了勾股定理,类比此方法研究等边三角形(如图②):在等边三角形ABC中,如果∠BAD=∠CBE=∠ACF,那么△ABD的三边存在一定的数量关系,设BD=a,AD=b,AB=c,则这三边a,b,c满足的数量关系是 .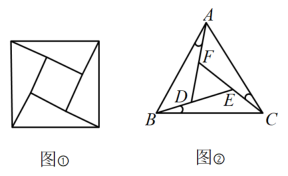
三、解答题
-
17. 已知数a,b,c在数轴上的位置如图所示:

化简:
18. 如图,在一次课外活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离,已知CD⊥BD,现测得AC= ,BC= ,CD= ,请计算A,B两个凉亭之间的距离. 19. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,求OE的长.
19. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,求OE的长.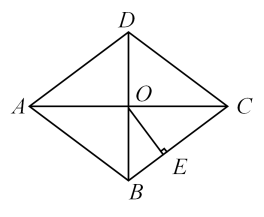 20. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示.
20. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系如图所示. (1)、A,B两城相距千米;(2)、当1≤t≤4时,求乙车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系式;(3)、乙车出发后小时追上甲车.21. 一家公司打算招聘一名英文翻译,对甲、乙两名应聘者进行了听、说、读、写的英语水平测试。他们的各项成绩(百分制)如下:
(1)、A,B两城相距千米;(2)、当1≤t≤4时,求乙车离开A城的距离y(km)与甲车行驶的时间t(h)之间的函数关系式;(3)、乙车出发后小时追上甲车.21. 一家公司打算招聘一名英文翻译,对甲、乙两名应聘者进行了听、说、读、写的英语水平测试。他们的各项成绩(百分制)如下:应聘者
听
说
读
写
甲
85
83
78
75
乙
73
80
85
82
如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比例确定,计算两名应聘者的成绩(百分制)。从他们的成绩看,应该录取谁?