浙江省绍兴市诸暨市2022年毕业生适应性考试数学试卷
试卷更新日期:2022-05-12 类型:中考模拟
一、选择题(本大题有10小题,每小题4分,共40分.)
-
1. 实数 中,最小的数是( )A、-2 B、0 C、1 D、2. 第七次全国人口普查数据显示,诸暨市常住人口约为1220000人,这个数字1220000用科学记数法可表示为( )A、 B、 C、 D、3. 如图所示的几何体是由七个相同的小正方体组合而成的,它的主视图是( )
 A、
A、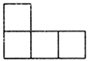 B、
B、 C、
C、 D、
D、 4. 已知现有的10瓶饮料中有2瓶已过了保质期,从这10瓶饮料中任取1瓶,恰好取到已过了保质期的饮料的概率是( )A、 B、 C、 D、5. 下面是一位同学做的四道题,其中正确的一题是( )A、 B、 C、 D、6. 已知 中有三个点在同一直线 上,不在此直线上的点是( )A、点P B、点Q C、点R D、点S7. 如图,在 中, 平分 交 于点 ,则 等于( )
4. 已知现有的10瓶饮料中有2瓶已过了保质期,从这10瓶饮料中任取1瓶,恰好取到已过了保质期的饮料的概率是( )A、 B、 C、 D、5. 下面是一位同学做的四道题,其中正确的一题是( )A、 B、 C、 D、6. 已知 中有三个点在同一直线 上,不在此直线上的点是( )A、点P B、点Q C、点R D、点S7. 如图,在 中, 平分 交 于点 ,则 等于( )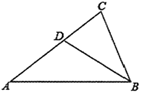 A、 B、 C、 D、8. 如图,将一张面积为50的大三角形纸片沿着虚线剪成三张小三角形纸片与一张矩形纸片.根据图中标示的长度,则矩形纸片的面积为( )
A、 B、 C、 D、8. 如图,将一张面积为50的大三角形纸片沿着虚线剪成三张小三角形纸片与一张矩形纸片.根据图中标示的长度,则矩形纸片的面积为( ) A、12 B、18 C、24 D、309. 如图,周长为定值的平行四边形 中, ,设 的长为 的长为y , 平行四边形 的面积为S . 当x在一定范围内变化时,y和S都随x的变化而变化,则y与 与x满足的函数关系分别是( )
A、12 B、18 C、24 D、309. 如图,周长为定值的平行四边形 中, ,设 的长为 的长为y , 平行四边形 的面积为S . 当x在一定范围内变化时,y和S都随x的变化而变化,则y与 与x满足的函数关系分别是( ) A、反比例函数关系,一次函数关系 B、反比例函数关系,二次函数关系 C、一次函数关系,反比例函数关系 D、一次函数关系,二次函数关系10. 现有一个 方格的小型跳棋盘,将8枚棋子摆成如图的“中”字形状,并规定每一步可移动一枚棋子进入相邻空格中,或可将某枚棋子跳过邻格中的一枚棋子而进入随后的空格中,同时将被其跳过的这枚棋子从棋盘上移走.若最终棋盘上只剩下一枚棋子并停在标有“国”字的空格中,则最少需要移动的步数是( )
A、反比例函数关系,一次函数关系 B、反比例函数关系,二次函数关系 C、一次函数关系,反比例函数关系 D、一次函数关系,二次函数关系10. 现有一个 方格的小型跳棋盘,将8枚棋子摆成如图的“中”字形状,并规定每一步可移动一枚棋子进入相邻空格中,或可将某枚棋子跳过邻格中的一枚棋子而进入随后的空格中,同时将被其跳过的这枚棋子从棋盘上移走.若最终棋盘上只剩下一枚棋子并停在标有“国”字的空格中,则最少需要移动的步数是( ) A、7 B、8 C、9 D、10
A、7 B、8 C、9 D、10二、填空题(本大题有6个小题,每小题5分,共30分)
-
11. 分解因式: .12. 有一圆柱形木材,埋在墙壁中,其横截面如图所示,测得木材的半径为 ,露在墙体外侧的弦长 ,其中半径 垂直平分 ,则埋在墙体内的弓形高 .
 13. 我国的《洛书》中记载着世界最古老的一个幻方:将九个数字填入 的方格中,使三行、三列、两对角线上的三个数之和都相等,根据如图的幻方,则代数式 .
13. 我国的《洛书》中记载着世界最古老的一个幻方:将九个数字填入 的方格中,使三行、三列、两对角线上的三个数之和都相等,根据如图的幻方,则代数式 .x
-2
y
0
14. 已知 中, ,在同一平面内,若 ,则 的长为 .15. 如图,已知直线 交x轴于点A , 交双曲线 于点B , 作直线 交直线 于点C , 交双曲线 于点D , 若 ,且 ,则 . 16. 正方形 的边长为4,点E是射线 上的一个动点,连结 ,以 为边往右侧作正方形 ,连结 .
16. 正方形 的边长为4,点E是射线 上的一个动点,连结 ,以 为边往右侧作正方形 ,连结 . (1)、当点E在 延长线上,且 时, .(2)、当点E在线段 上,且 为等腰三角形时, .
(1)、当点E在 延长线上,且 时, .(2)、当点E在线段 上,且 为等腰三角形时, .三、解答题(本大题有8小题,17~20题每小题8分,第21题10分,第22,23小题每小题12分,第24小题14分,共80分,)
-
17.(1)、计算:(2)、解不等式: .18. 在 两地之间有汽车站C , 甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶,甲、乙两车离C站的距离 (千米)与行驶时间x(小时)之间的函数图象如图所示.
 (1)、根据图形填空:甲车速度为千米/小时,乙车速度为千米/小时, 千米, 千米.(2)、甲、乙两车出发多少小时后相遇?19. 健康的体魄是青少年为祖国和人民服务的基本前提,是中华民族旺盛生命力的体现.某初中学校为了提高学生体质健康,制定合理的校园阳光体育锻炼方案,随机抽查了部分学生最近两周参加体育锻炼活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:请根据图中提供的信息,回答下列问题:
(1)、根据图形填空:甲车速度为千米/小时,乙车速度为千米/小时, 千米, 千米.(2)、甲、乙两车出发多少小时后相遇?19. 健康的体魄是青少年为祖国和人民服务的基本前提,是中华民族旺盛生命力的体现.某初中学校为了提高学生体质健康,制定合理的校园阳光体育锻炼方案,随机抽查了部分学生最近两周参加体育锻炼活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:请根据图中提供的信息,回答下列问题: (1)、抽查的学生中锻炼8天的有人.(2)、本次抽样调查的众数为 , 中位数为 .(3)、如果该校约有2000名学生,请你估计全校约有多少名学生参加体育锻炼的天数不少于7天?20. 图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点 均为可转动点,现测得 ,经多次调试发现当点 都在 的垂直平分线上时(如图3所示)放置最平稳.
(1)、抽查的学生中锻炼8天的有人.(2)、本次抽样调查的众数为 , 中位数为 .(3)、如果该校约有2000名学生,请你估计全校约有多少名学生参加体育锻炼的天数不少于7天?20. 图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点 均为可转动点,现测得 ,经多次调试发现当点 都在 的垂直平分线上时(如图3所示)放置最平稳.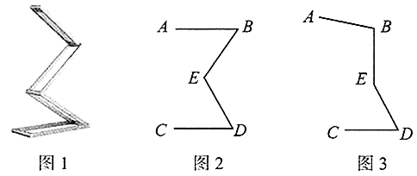 (1)、求放置最平稳时灯座 与灯杆 的夹角的大小;(2)、当A点到水平桌面( 所在直线)的距离为 时,台灯光线最佳,能更好的保护视力.若台灯放置最平稳时,将 调节到 ,试通过计算说明此时光线是否为最佳.(参考数据: )21. 如图, 为 的直径,点B是 上方半圆上的一点,作 平分 交 于点D , 过点D作 交 的延长线于点E .
(1)、求放置最平稳时灯座 与灯杆 的夹角的大小;(2)、当A点到水平桌面( 所在直线)的距离为 时,台灯光线最佳,能更好的保护视力.若台灯放置最平稳时,将 调节到 ,试通过计算说明此时光线是否为最佳.(参考数据: )21. 如图, 为 的直径,点B是 上方半圆上的一点,作 平分 交 于点D , 过点D作 交 的延长线于点E .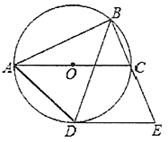 (1)、求证: 是 的切线;(2)、若 ,求 的长.22. 如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米,当喷射出的水流与喷灌架的水平距离为10米时,达到最大高度6米,现将喷灌架置于坡地底部点O处,草坡上距离O的水平距离为15米处有一棵高度为1.2米的小树 垂直水平地面且A点到水平地面的距离为3米.
(1)、求证: 是 的切线;(2)、若 ,求 的长.22. 如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米,当喷射出的水流与喷灌架的水平距离为10米时,达到最大高度6米,现将喷灌架置于坡地底部点O处,草坡上距离O的水平距离为15米处有一棵高度为1.2米的小树 垂直水平地面且A点到水平地面的距离为3米. (1)、计算说明水流能否浇灌到小树后面的草地.(2)、记水流的高度为 ,斜坡的高度为 ,求 的最大值.(3)、如果要使水流恰好喷射到小树顶端的点B , 那么喷射架应向后平移多少米?
(1)、计算说明水流能否浇灌到小树后面的草地.(2)、记水流的高度为 ,斜坡的高度为 ,求 的最大值.(3)、如果要使水流恰好喷射到小树顶端的点B , 那么喷射架应向后平移多少米?


