浙江省金华市永康市2022年中考适应性考试数学试卷

试卷更新日期：2022-05-12 类型：中考模拟

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 2022的相反数是（）

A、 $\frac{1}{2022}$ B、 $- \frac{1}{2022}$ C、2022 D、-2022

查看试题解析
2. 世界卫生组织4月14日公布的最新数据显示，全球累计新冠肺炎确诊病例超过499 000 000例，将数据499 000 000用科学记数法表示为（）

A、 $4.99 \times 10^{7}$ B、 $4.99 \times 10^{8}$ C、 $49.9 \times 10^{7}$ D、 $0.499 \times 10^{9}$

查看试题解析
3. 五位同学800米跑步成绩各不相同，统计时出现了一处错误：将最高成绩写得更高了.下列计算结果中不受影响的是（）

A、方差 B、标准差 C、中位数 D、平均数

查看试题解析
4. 如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图中，既是轴对称图形，又是中心对称图形的是（）

A、主视图 B、左视图 C、俯视图 D、主视图和左视图

查看试题解析
5. 已知抛物线 $y = - x^{2} + m x - m + 2$ 过点（2，2），则m的值为（）

A、1 B、4 C、3 D、0

查看试题解析
6. 如图，线段AB是⊙O的直径，点C在圆上， $∠ A O C = 60 °$ ，点P是线段AB延长线上的一点，连结PC，则 $∠ A P C$ 的度数不可能是（）

A、 $30 °$ B、 $25 °$ C、 $10 °$ D、 $5 °$

查看试题解析
7. 已知 $a$ 是方程 $2 x^{2} - 3 x - 5 = 0$ 的一个解，则 $- 4 a^{2} + 6 a$ 的值为（）

A、10 B、－10 C、2 D、－40

查看试题解析
8. 如图，在矩形ABCD中，AB=2，AD=4，E为CD的中点，连结AE并延长，交BC的延长线于点F，点P为BC上一点，当∠PAE=∠DAE时，则AP的长度为（）

A、 $\frac{15}{4}$ B、 $\frac{17}{4}$ C、4 D、 $\frac{9}{2}$

查看试题解析
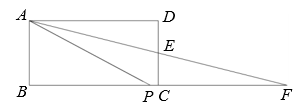9. 唐代大诗人李白喜好饮酒作诗，民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云：今携一壶酒，游春郊外走.逢朋加一倍，入店饮斗九.相逢三处店，饮尽壶中酒.试问能算士：如何知原有.
大意是：李白在郊外春游时，遇见一个朋友，先将壶里的酒增加一倍，再喝掉其中的19升酒.按照这样的约定，在第3次遇到朋友后正好喝光了壶中的酒，设壶中原有酒为x升，则可列出方程为（）

A、 $2 x - 19 = 0$ B、 $2 (2 x - 19) - 19 = 0$ C、 $2 (2 x + 19) - 19 = 0$ D、 $2 [2 (2 x - 19) - 19] - 19 = 0$

查看试题解析
10. 用正方形纸片剪出一副七巧板，并将其拼成如图的“小天鹅”，设小天鹅的水平宽度为l（左右最大距离），铅垂高度为h（上下最大距离），则 $\frac{h}{l}$ 的值为（）

A、 $\frac{7}{5}$ B、 $\frac{5}{7}$ C、 $\frac{2 + 2 \sqrt{2}}{7}$ D、 $\frac{7 \sqrt{2} - 7}{2}$

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 若分式 $\frac{1}{x - 3}$ 有意义，则x的取值范围为．

查看试题解析
12. 因式分解： $3 a^{2} - 6 a + 3$ ＝．

查看试题解析
13. 在不透明的纸盒中装有3个红球和2个黄球(除颜色外其余均相同)，现从中任意摸出一个球，则摸到红球的概率为．

查看试题解析
14. 现有A，B，C三种型号的纸片若干张，大小如图所示.从中取出一些纸片进行无空隙、无重叠拼接，拼成一个长宽分别为11和5的新矩形，在各种拼法中，B型纸片最多用了张.

查看试题解析
15. 如图所示，在矩形纸片ABCD中，点M是对角线AC的中点，点E是AB上一点，把△DEC沿直线DE折叠，得△DEF，点F恰好落在射线CA上.若MF=AB，则∠DAF=°.

查看试题解析
16. 图1是修正带实物图，图2是其示意图，使用时⊙B上的白色修正物随透明条（载体）传送到点O处进行修正，留下来的透明条传到⊙A收集. 即透明条的运动路径为： M→C→O→P→N.假设O，P，A，B在同一直线上，BC=3cm，AC=4cm，AC⊥BC，tan∠ACO= $\frac{1}{3}$ ，P为OA中点.

(1)、点B到OC的距离为cm．

(2)、若⊙A的半径为1cm，当留下的透明条从点O出发，第一次传送到⊙A上某点，且点B到该点距离最小时，最多可以擦除的长度为cm.

查看试题解析

三、解答题（本题有8小题，共66分，）

17. 计算： ${(\frac{1}{4})}^{- 1} - 6 \tan 30 ° + \sqrt{12} - | - 1 |$ $.$

查看试题解析
18. 解不等式组： $\{\begin{cases} 4 x + 7 ＞ 2 x - 3 \\ \frac{3 x - 6}{2} ＜ x \end{cases}$ $.$

查看试题解析
19. 如图，在6×6的方格纸中，每个小正方形的顶点称为格点，请仅用直尺分别按要求画出三个顶点都是格点的三角形 (每小题只需画一个) ．

(1)、在图1中画△ABD，使AB=AD.

(2)、在图2中画△ABC，使 $A B = \sqrt{5} B C$ ，且∠ACB=90°.

查看试题解析

20. 某校组织了七年级500名学生参加“创青春冬奥知识竞赛”竞赛，随机抽取了50份竞赛卷进行统计，发现最低分为65分，最高分为100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：

组别	成绩x分	人数
A	95≤x≤100	8
B	85≤x＜95	m
C	75≤x＜85	n
D	65≤x＜75	3

(1)、m＝.

(2)、求C组所占圆心角度数.

(3)、该校对成绩为95≤x≤100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1∶3∶6，请估算七年级获得二等奖的学生人数．

查看试题解析

21. 在平面直角坐标系中，如图为一根木料的横截面示意图，其中的曲线AB是一段反比例函数图象，线段AB所在直线与x轴相交所成的锐角为45°，端点B的坐标是（80，20）.

(1)、求该反比例函数解析式.

(2)、求线段AB所在直线的解析式.

(3)、木工想把该木料分割成完全相同的两部分.试求该横截面上的分割线长.

查看试题解析
22. 已知点E是正方形ABCD的边AB上一点，AB= $3 \sqrt{2}$ ，BE=2.以BE为边向右侧作正方形BEFG，将正方形BEFG绕点B顺时针旋转 $α$ 度(0≤ $α$ ≤90°)，连结AE，CG （如图）.

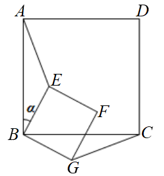
（参考数据： $\sin 28 ° \approx \frac{\sqrt{2}}{3}$ ， $\sin 62 ° \approx \frac{\sqrt{7}}{3}$ ， $\tan 28 ° \approx \frac{\sqrt{14}}{7}$ ， $\tan 62 ° \approx \frac{\sqrt{14}}{2}$ ）

(1)、求证：△ABE≌△CBG.

(2)、当点E在BD上时，求CG的长.

(3)、当 $∠ A E B = 90 °$ 时，正方形BEFG停止旋转，求在旋转过程中线段AE扫过的面积.

查看试题解析
23. 阅读材料：一般地，对于某个函数，如果自变量x在取值范围内任取x=a与x= $- a$ 时，函数值相等，那么这个函数是“对称函数”.例如：y=x² ，在实数范围内任取x=a时，y=a²；当x= $- a$ 时，y= ${(- a)}^{2}$ = a² ，所以y=x²是“对称函数”.

(1)、函数 $y = 2 | x | + 1$ ▲ 对称函数（填“是”或“不是”）.当x≥0时， $y = 2 | x | + 1$ 的图象如图1所示，请在图1中画出x＜0时， $y = 2 | x | + 1$ 的图象.

(2)、函数 $y = x^{2} - 2 | x | + 1$ 的图象如图2所示，当它与直线y=-x+n恰有3个交点时，求n的值.

(3)、如图3，在平面直角坐标系中，矩形ABCD的顶点坐标分别是A（-3，0），B（2，0），C（2，-3），D（-3，-3），当二次函数 $y = x^{2} - b | x | + 1$ （b>0）的图象与矩形的边恰有4个交点时，求b的取值范围.

查看试题解析
24. 已知AC是平行四边形ABCD的一条对角线，且AB=AC，⊙O是 $Δ A B C$ 的外接圆，CD与⊙O的另一个交点为E，连结AE.

(1)、当点E在线段CD上时，如图1.
①求证： $Δ A B C$ ∽ $Δ A E D .$

②若 $\tan ∠ A B C = 3$ ， $Δ A E C$ 的面积为 $\frac{81}{5}$ ，求⊙O的半径.

(2)、当点E在直线CD上时，过点E作EH⊥AB于H，直线EH与直线BC交于点F. 如图2，若 $C E = \frac{1}{2} H E$ 时，求 $\frac{S_{Δ A B C}}{S_{Δ C E F}}$ 的值.

查看试题解析