浙江省温岭市2022学年初中毕业学业模拟考试数学试卷
试卷更新日期:2022-05-12 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分。请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
-
1. 下列各数中比-1小的数是( )A、 B、 C、0 D、22. 如图是由四个相同的小正方体组成的一个立体图形,其主视图是( )
 A、
A、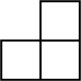 B、
B、 C、
C、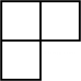 D、
D、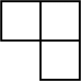 3. 下列各式运算正确的是( )A、x2+x3=x5 B、x3-x2=x C、x2·x3=x6 D、(x3)2=x64. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间5. 将一块含有45°角的直角三角板和一把直尺按如图所示方式摆放,若∠1=95°,则∠2的度数是( )
3. 下列各式运算正确的是( )A、x2+x3=x5 B、x3-x2=x C、x2·x3=x6 D、(x3)2=x64. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间5. 将一块含有45°角的直角三角板和一把直尺按如图所示方式摆放,若∠1=95°,则∠2的度数是( ) A、65° B、55° C、50° D、45°6. 受新冠肺炎疫情影响,某企业生产总值从2月份的300万元,连续降低至4月份的260万元,设平均每月降低率为x,则可列方程( )A、300(1+x)2=260 B、300(1-x)2=260 C、300(1-x2)=260 D、300(1-2x)=2607. 如图,⊙O过A、B两点,交BC于点D,AC是切线,连接OD,若∠C=∠ODB=30°,若BD=4 ,则 的长为( )
A、65° B、55° C、50° D、45°6. 受新冠肺炎疫情影响,某企业生产总值从2月份的300万元,连续降低至4月份的260万元,设平均每月降低率为x,则可列方程( )A、300(1+x)2=260 B、300(1-x)2=260 C、300(1-x2)=260 D、300(1-2x)=2607. 如图,⊙O过A、B两点,交BC于点D,AC是切线,连接OD,若∠C=∠ODB=30°,若BD=4 ,则 的长为( ) A、π B、2π C、3π D、8π8.
A、π B、2π C、3π D、8π8.
如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于 AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( ) A、 B、2 C、2 -2 D、 +19. 如图,网格格点上三点A,B,C在某平面直角坐标系中的坐标分别为(a,b)、(c,d).(a+c,b+d),则下列判断错误的是( )
A、 B、2 C、2 -2 D、 +19. 如图,网格格点上三点A,B,C在某平面直角坐标系中的坐标分别为(a,b)、(c,d).(a+c,b+d),则下列判断错误的是( ) A、a<0 B、b=2d C、a+c=b+d D、a+b+d=c10. 如图,边长为1的正方形ABCD沿着过中心O的直线EF (EF不为对角线)对折,下列结论不正确的是( )
A、a<0 B、b=2d C、a+c=b+d D、a+b+d=c10. 如图,边长为1的正方形ABCD沿着过中心O的直线EF (EF不为对角线)对折,下列结论不正确的是( ) A、△DHF的周长为定值 B、∠HOF的度数为定值 C、四边形HCNO的面积为定值 D、△NOE的面积为定值11. 因式分解:x2-4x= 。12. 化简: =13. 如图,受疫情影响,学生就餐采取隔板阻挡,若小赵、小李、小王、小陈四人同桌就餐,那么小赵和小李坐在对面的概率是
A、△DHF的周长为定值 B、∠HOF的度数为定值 C、四边形HCNO的面积为定值 D、△NOE的面积为定值11. 因式分解:x2-4x= 。12. 化简: =13. 如图,受疫情影响,学生就餐采取隔板阻挡,若小赵、小李、小王、小陈四人同桌就餐,那么小赵和小李坐在对面的概率是 14. 如图,等腰直角三角形ABC,∠C=90°,点D、E分别是AB、BC上的点,且DC=DE,AD=BE= ,则图中阴影部分的面积为
14. 如图,等腰直角三角形ABC,∠C=90°,点D、E分别是AB、BC上的点,且DC=DE,AD=BE= ,则图中阴影部分的面积为 15. 如图,在平面直角坐标系中,直线y=kx+3与x轴、y轴交于A、B两点,与双曲线y= (x>0)交于C点,若AB=BC,则k的值为 .
15. 如图,在平面直角坐标系中,直线y=kx+3与x轴、y轴交于A、B两点,与双曲线y= (x>0)交于C点,若AB=BC,则k的值为 . 16. 如图,AB是⊙O的弦,AB=4 ,点P是优弧APB上的动点,∠P=45°,连接PA、PB,AC是△ABP的中线,(1)若∠CAB=∠P,则AC= ;(2)AC的最大值=
16. 如图,AB是⊙O的弦,AB=4 ,点P是优弧APB上的动点,∠P=45°,连接PA、PB,AC是△ABP的中线,(1)若∠CAB=∠P,则AC= ;(2)AC的最大值=
二、解答题(第17~20题,每题8分,第21题10分,第22~23题, 每题12分,第24题14分,共80分)
-
17. 计算:|2- |- +2022018. 解方程组19. 如图所示是国际标准的篮球架,某兴趣小组想知道篮筐中心A到地面的高度,现测得如下数据:CD垂直于地面,CD=255cm,BC=90cm,AB平行于地面,∠ABC=145°,请你利用学过的知识帮他们求出该高度.(结果精确到1cm,参考数据:sin35°=0.57,cos35°=0.82 tan35°=0.70)
 20. 某中学八年级甲、乙两班分别选5名同学参加“防疫宣传”演讲比赛,其预赛成绩如图所示:
20. 某中学八年级甲、乙两班分别选5名同学参加“防疫宣传”演讲比赛,其预赛成绩如图所示:
平均数
中位数
众数
方差
甲班
8.5
8.5
0.7
乙班
8.5
10
1.6
(1)、根据左图填写右表空格;(2)、根据上表数据,请你任选-组统计量描述两个班的成绩水平?(3)、乙班小明说:“我的成绩是中等水平”,你知道他是几号选手吗?21. 为了做好近视防控工作,及时掌握学生视力健康状况,市教育局在某校开展了“爱眼护眼”视力检测活动,学校共有700人,开始时用一台仪器进行检测,未检测的人数记为y,检测时间为t小时,现记录有关数据如下:t/时间(h)
1
2
2.5
3
b
……
y/人数
660
620
600
a
500
……
(1)、直接写出表中a、b的值:a= , b= ;(2)、根据表中数据,用你学过的函数解析式描述y与t的关系(不要求写出t的范围);(3)、检测上午8:00点开始,至下午13:00点时,学校为了在下午17:00之前完成检测,增加了若干台相同的仪器同时进行检测(每台仪器的工作效率相同),问至少需要增加多少台仪器?22. 抛物线y=ax2+bx+c经过A(0,4)和B(2,0)两点.(1)、求c的值及a,b满足的关系式;(2)、抛物线同时经过两个不同的点M (k,m)和N(-2-k,m),求b的值:(3)、若抛物线在A和B两点间y随x的增大而减少,求a的取值范围.23. 在Rt△ABC中,∠A=90°,AB= AC,BC=6.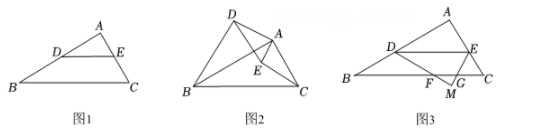 (1)、如图1,D是AB上一点,DE∥BC,交AC于E点,则BD,CE的数量关系为;(2)、如图2,将(1)中△ADE绕着点A顺时针旋转,旋转角为α(0°<α<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由;(3)、如图3,将(1)中△ADE沿DE对折,A的对应点是M,使点M在BC下方,△MDE与Rt△ABC重叠部分面积记为y,BD的长记为x,求y关于x的函数关系式,并求y的最大值.24. 如图,平行四边形ABCD,⊙O是△BCD的外接圆,交直线AB、直线AD于点E、F,连接CE、CF,
(1)、如图1,D是AB上一点,DE∥BC,交AC于E点,则BD,CE的数量关系为;(2)、如图2,将(1)中△ADE绕着点A顺时针旋转,旋转角为α(0°<α<90°),连接CE,BD,请问(1)中BD,EC的数量关系还成立吗?说明理由;(3)、如图3,将(1)中△ADE沿DE对折,A的对应点是M,使点M在BC下方,△MDE与Rt△ABC重叠部分面积记为y,BD的长记为x,求y关于x的函数关系式,并求y的最大值.24. 如图,平行四边形ABCD,⊙O是△BCD的外接圆,交直线AB、直线AD于点E、F,连接CE、CF,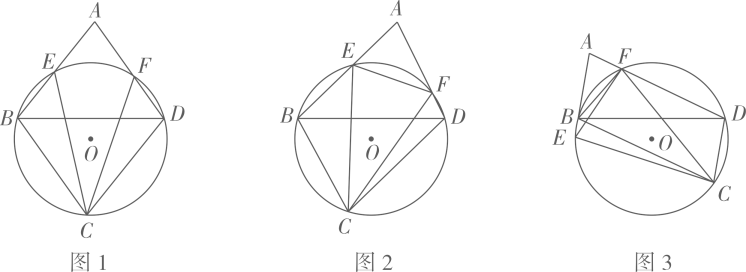 (1)、如图1,若平行四边形ABCD是菱形,求证:CE=CF;(2)、如图2,若∠A=70°,求∠ECF的度数;(3)、若BD=4 ,⊙O半径为3,
(1)、如图1,若平行四边形ABCD是菱形,求证:CE=CF;(2)、如图2,若∠A=70°,求∠ECF的度数;(3)、若BD=4 ,⊙O半径为3,①如图2,连接EF,求EF的长;
②如图3,连接EF、BF,若BF=3BE,请直接写出△BCF的面积 ▲ .